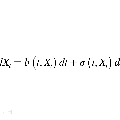分数阶时滞随机微分方程中的随机共振现象与行为研究

项目名称： 分数阶时滞随机微分方程中的随机共振现象与行为研究

项目编号： No.11501386

项目类型： 青年科学基金项目

立项/批准年度： 2016

项目学科： 数理科学和化学

项目作者： 钟苏川

作者单位： 四川大学

项目金额： 18万元

中文摘要： 本项目研究“分数阶时滞随机微分方程中的随机共振现象与行为”，属于有重大实际需求驱动和广泛实际背景的数学前沿应用基础研究。具体内容是：分数阶线性时滞随机微分方程的随机共振现象产生机理及其参数相依性；交叉耦合作用下分数阶时滞随机微分方程的随机共振现象；分数阶非线性时滞随机微分方程的随机共振现象与行为研究。. 20世纪80年代随机共振提出以来，即被尝试用于解决各种物理、化学、生物和工程中的实际问题，许多模型也被证实能够产生随机共振现象。整数阶时滞随机微分方程的随机共振现象的研究，近年来逐渐成为数学和力学的研究热点。然而，对于分数阶时滞随机微分方程的相关研究还处于起步阶段，许多问题亟待解决。本项目从数学和力学角度出发，深入研究分数阶时滞随机微分方程的解析解和数值解，进而研究其随机共振现象的产生机理及参数相依性，建立严格的数学理论，为后续工程应用奠定基础。

中文关键词： 分数阶；随机微分方程；随机共振；时滞

英文摘要： This project research in “the stochastic resonance in fractional stochastic differential equation with time delay”, which is one of the basic mathematical frontiers driven by widely and important needs. The project includes: Exploring the mechanism of a linear fractional stochastic differential equation with time delay and research the influence of the parameters on the system; Effects of cross-correlation intensity between noises on stochastic resonance of a linear fractional stochastic differential equation with time delay; The stochastic resonance of a nonlinear fractional stochastic differential equation with time delay..Since first introduced in 1980s, the stochastic resonance has been demonstrated to be existed in lots of models, and effect in solving a variety of physical, chemical, biological and engineering problems. The research of stochastic resonance phenomenon in a integer stochastic differential equation with time delay has become a hot area in mathematics and mechanics studies recent years. However, the related research in the fractional stochastic differential equation with time delay are still in its initial stage and there’re many problems to be explored. This project plans to have a deep study in the analytic and numerical solutions of the fractional stochastic differential equation with time delay from the viewpoint of mathematics and mechanics. And furthermore, by exploring the mechanism of system and influence of the parameters, we hope we could build a strict mathematical theory of the problem and lay a foundation for future engineering applications.

英文关键词： Fractional ;Stochastic Differential Equation;Stochastic Resonance;Time Delay