On a Dynamic Variant of the Iteratively Regularized Gauss-Newton Method with Sequential Data

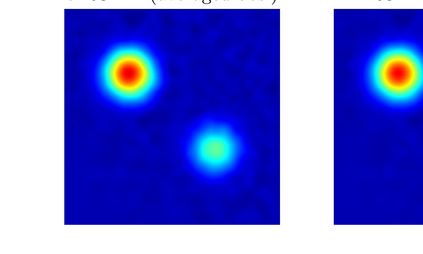
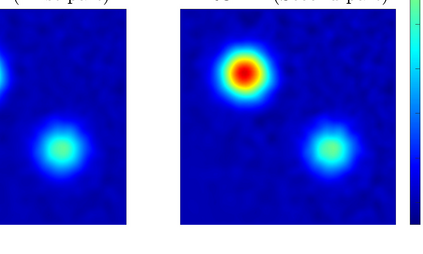
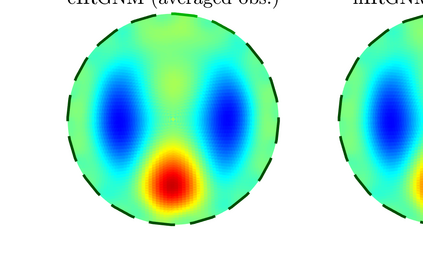
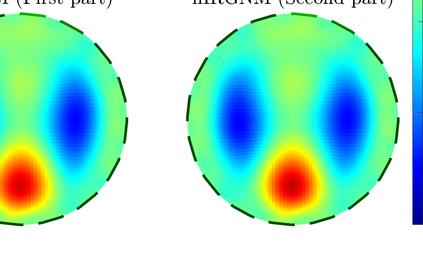
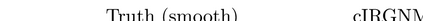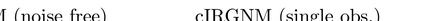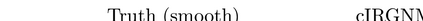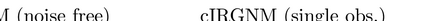For numerous parameter and state estimation problems, assimilating new data as they become available can help produce accurate and fast inference of unknown quantities. While most existing algorithms for solving those kind of ill-posed inverse problems can only be used with a single instance of the observed data, in this work we propose a new framework that enables existing algorithms to invert multiple instances of data in a sequential fashion. Specifically we will work with the well-known iteratively regularized Gauss-Newton method (IRGNM), a variational methodology for solving nonlinear inverse problems. We develop a theory of convergence analysis for a proposed dynamic IRGNM algorithm in the presence of Gaussian white noise. We combine this algorithm with the classical IRGNM to deliver a practical (hybrid) algorithm that can invert data sequentially while producing fast estimates. Our work includes the proof of well-definedness of the proposed iterative scheme, as well as various error bounds that rely on standard assumptions for nonlinear inverse problems. We use several numerical experiments to verify our theoretical findings, and to highlight the benefits of incorporating sequential data. The context of the numerical experiments comprises various parameter identification problems including a Darcy flow elliptic PDE example, and that of electrical impedance tomography.