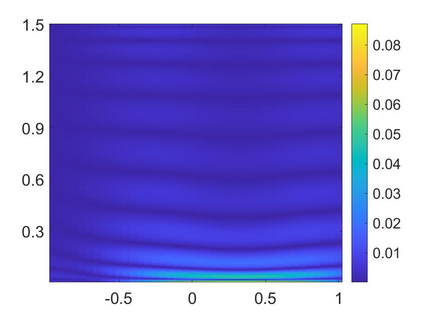
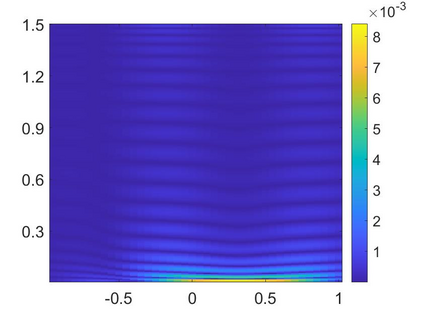
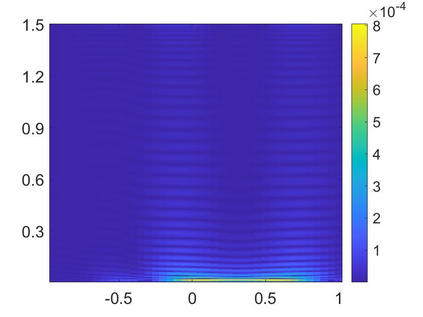
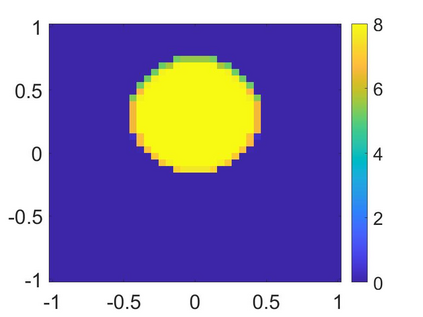
We propose to combine the Carleman estimate and the Newton method to solve an inverse source problem for nonlinear parabolic equations from lateral boundary data. The stability of this inverse source problem is conditionally logarithmic. Hence, numerical results due to the conventional least squares optimization might not be reliable. In order to enhance the stability, we approximate this problem by truncating the high frequency terms of the Fourier series that represents the solution to the governing equation. By this, we derive a system of nonlinear elliptic PDEs whose solution consists of Fourier coefficients of the solution to the parabolic governing equation. We solve this system by the Carleman-Newton method. The Carleman-Newton method is a newly developed algorithm to solve nonlinear PDEs. The strength of the Carleman-Newton method includes (1) no good initial guess is required and (2) the computational cost is not expensive. These features are rigorously proved. Having the solutions to this system in hand, we can directly compute the solution to the proposed inverse problem. Some numerical examples are displayed.
翻译:我们提议将Carleman估计值和Newton方法结合起来,以解决横向边界数据中非线性抛物线方程式的反源源问题。 反源问题的稳定性是有条件的对数。 因此, 常规最小平方优化导致的数字结果可能不可靠。 为了增强稳定性, 我们通过缩短代表治理方程式解决方案的Fourier系列的高频条件来比较这一问题。 通过这个方法, 我们得出了一个非线性椭圆形 PDE 系统, 其解决方案包括参数方程式的Fourier系数。 我们用 Carleman- Newton 方法解决了这个系统。 Carleman- Newton 方法是解决非线性 PDEs的新开发的算法。 Carleman- Newton 方法的强度包括:(1) 没有良好的初步猜测, 并且 (2) 计算成本不昂贵。 这些特征得到了严格证明。 有了这个系统的解决方案, 我们就可以直接将解决方案编译为反向问题的解决方案。 某些数字示例被展示 。