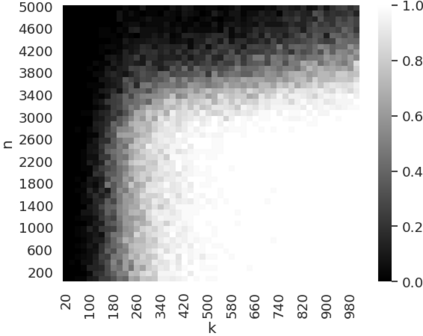
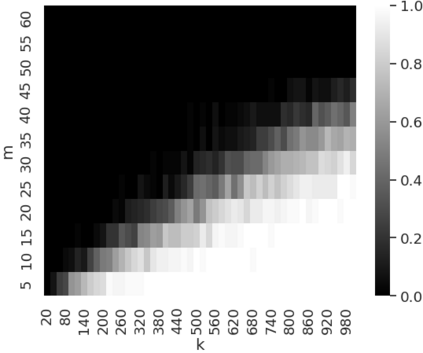
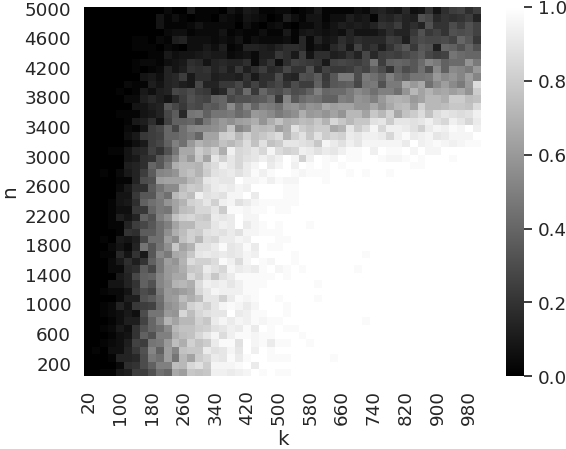
Neural networks have become a prominent approach to solve inverse problems in recent years. Amongst the different existing methods, the Deep Image/Inverse Priors (DIPs) technique is an unsupervised approach that optimizes a highly overparametrized neural network to transform a random input into an object whose image under the forward model matches the observation. However, the level of overparametrization necessary for such methods remains an open problem. In this work, we aim to investigate this question for a two-layers neural network with a smooth activation function. We provide overparametrization bounds under which such network trained via continuous-time gradient descent will converge exponentially fast with high probability which allows to derive recovery prediction bounds. This work is thus a first step towards a theoretical understanding of overparametrized DIP networks, and more broadly it participates to the theoretical understanding of neural networks in inverse problem settings.
翻译:近年来,神经网络已成为解决反问题的一种突出方法。在不同的现有方法中,深度图像/反先验(DIP)技术是一种无监督方法,它通过优化高度过参数化的神经网络,将随机输入转换为一个对象,其在正演模型下的图像与观测相匹配。然而,对于这样的方法所需要的超参数化程度仍然是一个未解决的问题。在本文中,我们旨在研究具有平滑激活函数的两层神经网络的这个问题。我们提供了一些超参数化下限,对于这样的网络,通过连续时间梯度下降训练,将在高概率下指数级快速收敛,这可以得到恢复预测的下降界。因此,这项工作是向理解超参数化DIP网络迈出的第一步,更广泛地参与了神经网络在反问题设置中的理论理解。