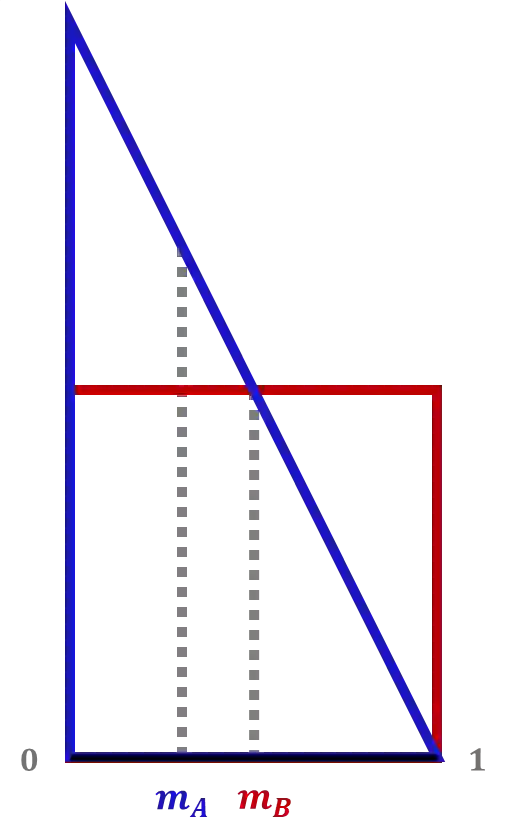
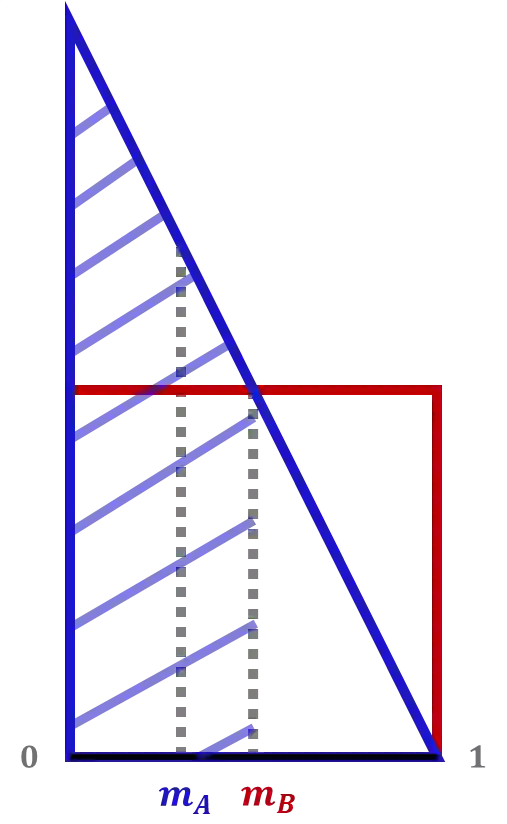
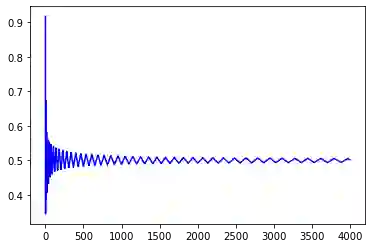
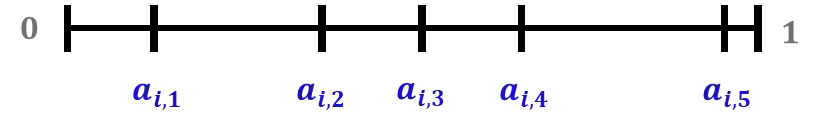We consider the setting of repeated fair division between two players, denoted Alice and Bob, with private valuations over a cake. In each round, a new cake arrives, which is identical to the ones in previous rounds. Alice cuts the cake at a point of her choice, while Bob chooses the left piece or the right piece, leaving the remainder for Alice. We consider two versions: sequential, where Bob observes Alice's cut point before choosing left/right, and simultaneous, where he only observes her cut point after making his choice. The simultaneous version was first considered by Aumann and Maschler (1995). We observe that if Bob is almost myopic and chooses his favorite piece too often, then he can be systematically exploited by Alice through a strategy akin to a binary search. This strategy allows Alice to approximate Bob's preferences with increasing precision, thereby securing a disproportionate share of the resource over time. We analyze the limits of how much a player can exploit the other one and show that fair utility profiles are in fact achievable. Specifically, the players can enforce the equitable utility profile of $(1/2, 1/2)$ in the limit on every trajectory of play, by keeping the other player's utility to approximately $1/2$ on average while guaranteeing they themselves get at least approximately $1/2$ on average. We show this theorem using a connection with Blackwell approachability. Finally, we analyze a natural dynamic known as fictitious play, where players best respond to the empirical distribution of the other player. We show that fictitious play converges to the equitable utility profile of $(1/2, 1/2)$ at a rate of $O(1/\sqrt{T})$.
翻译:暂无翻译