A Well-balanced Point-Average-Moment PolynomiAl-interpreted (PAMPA) Method for Shallow Water Equations with Horizontal Temperature Gradients

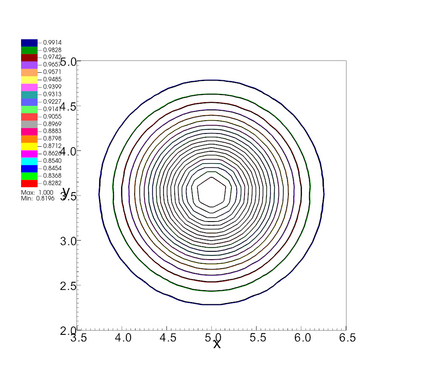
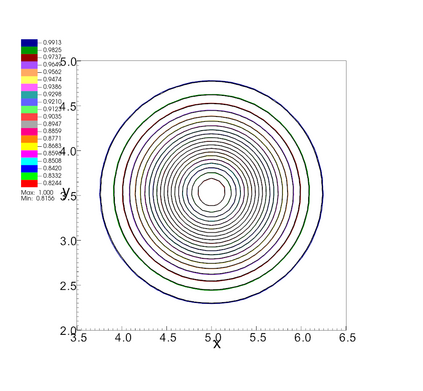
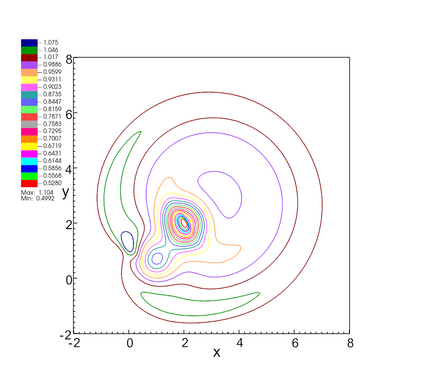
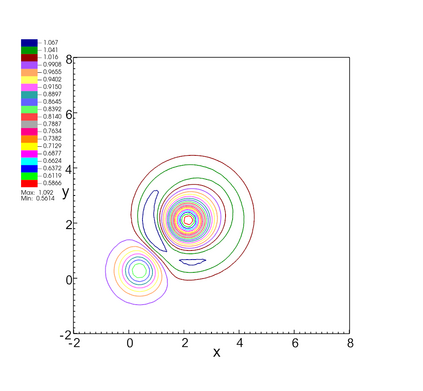
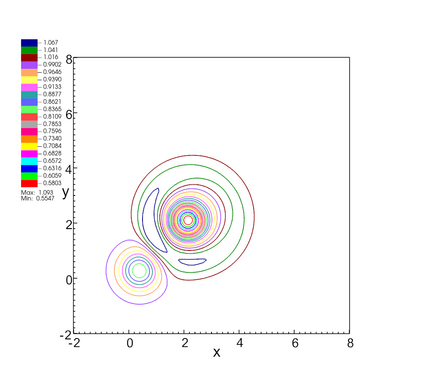
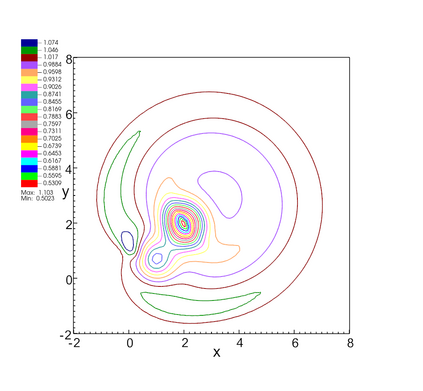
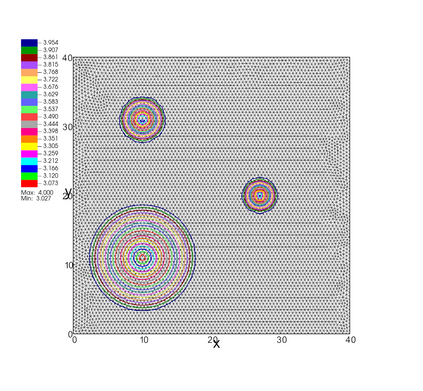
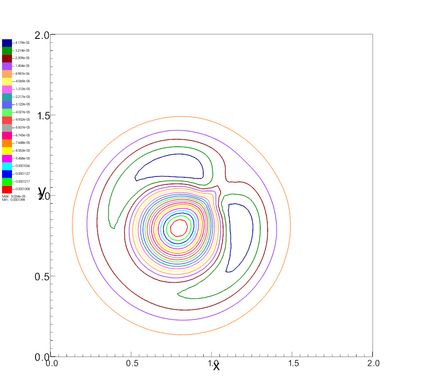
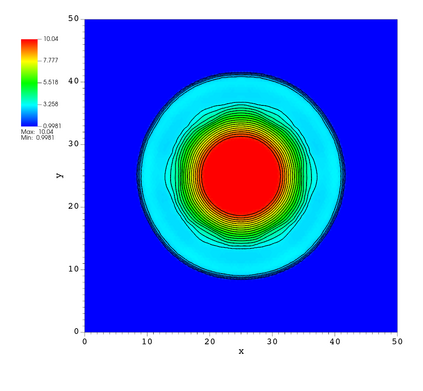
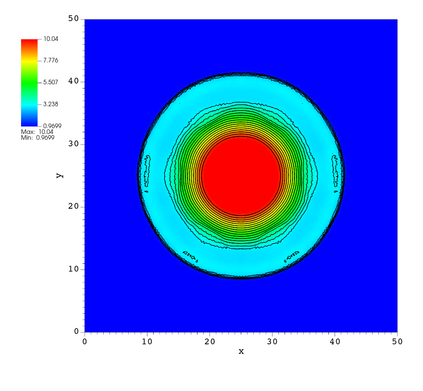
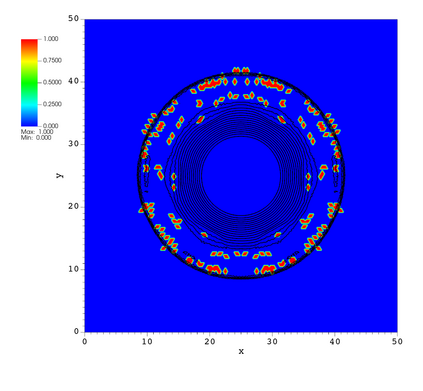
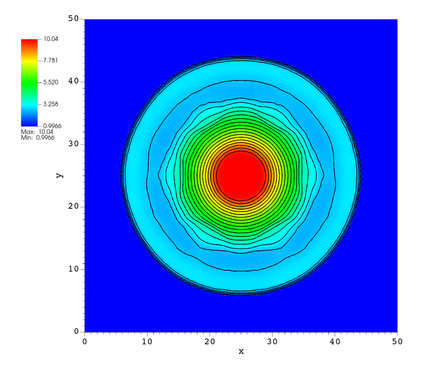
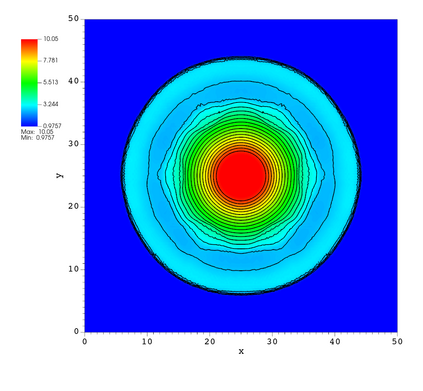
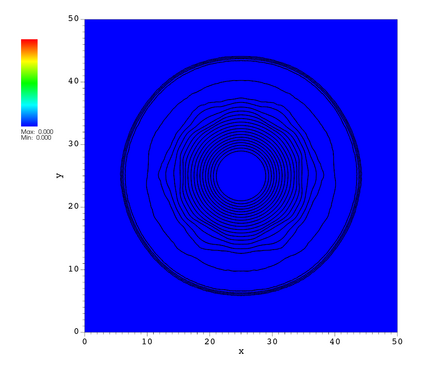
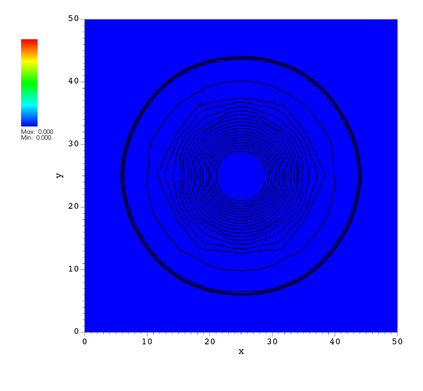
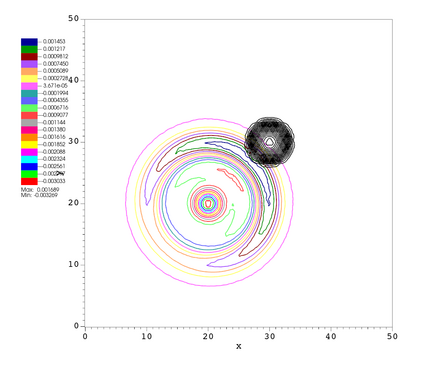
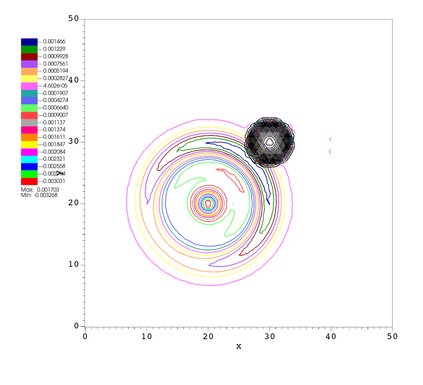
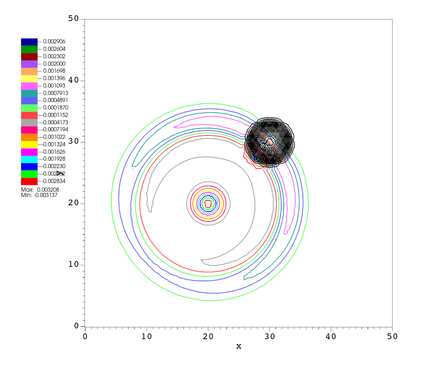
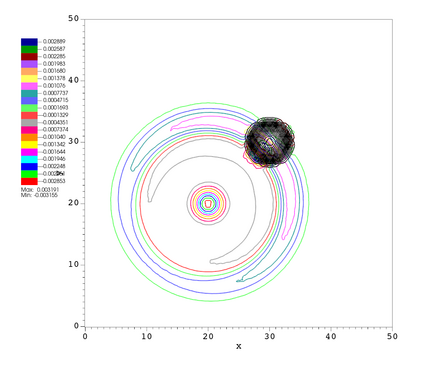
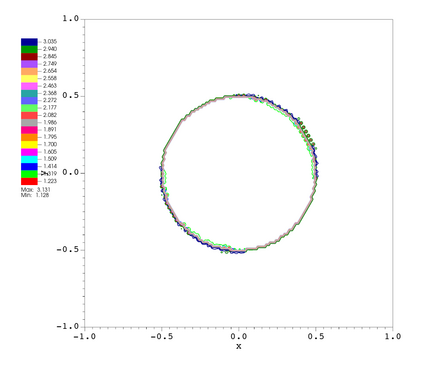
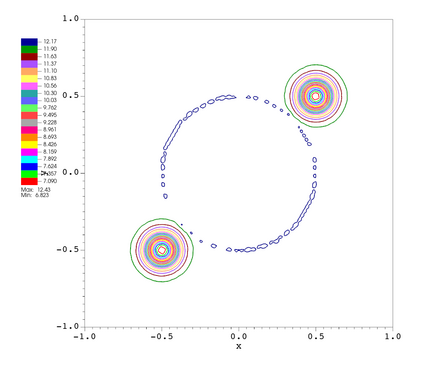
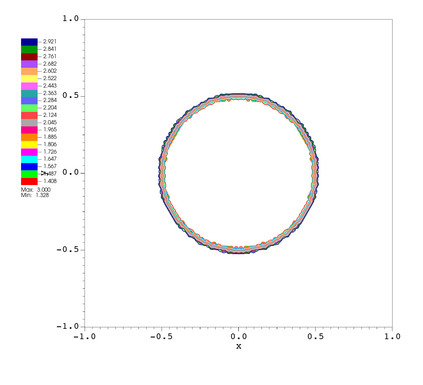
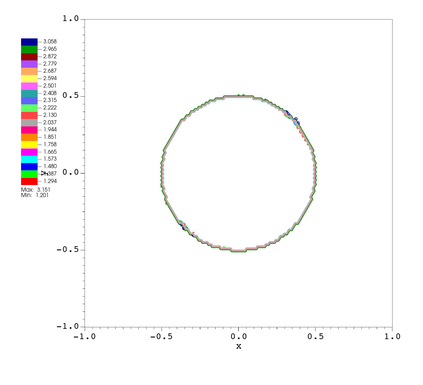
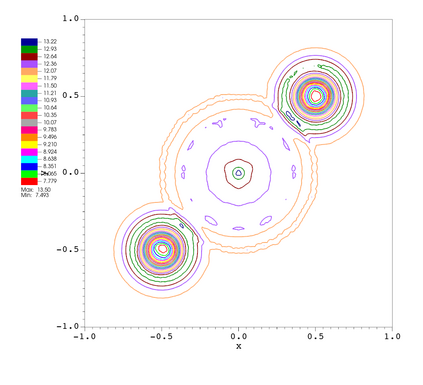
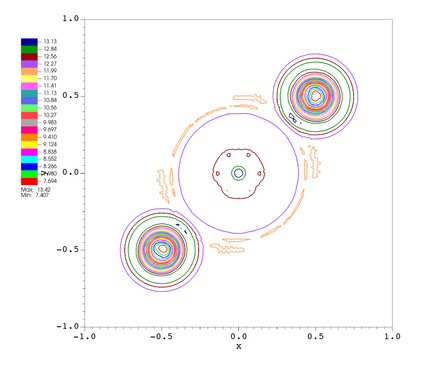
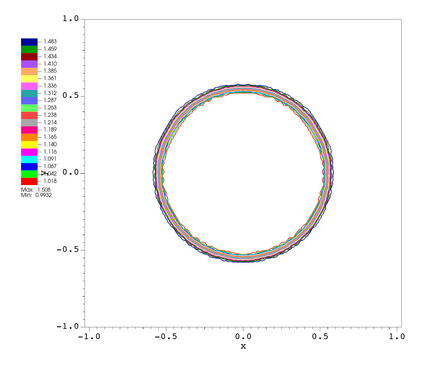
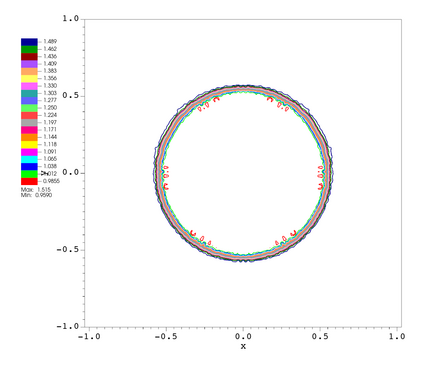
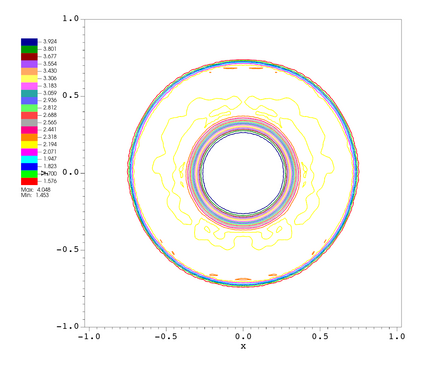
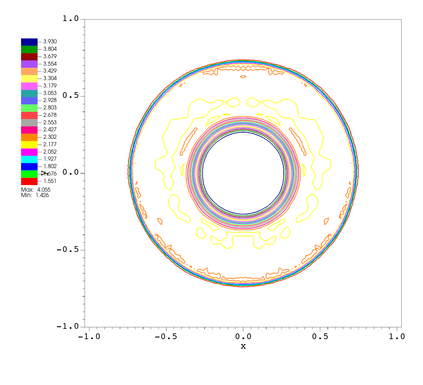
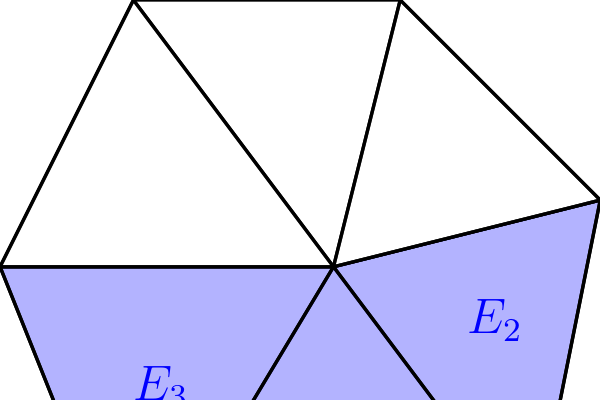
In this paper, we develop a novel well-balanced Point-Average-Moment PolynomiAl-interpreted (PAMPA) numerical method for solving the two-dimensional shallow water equations with temperature gradients on unstructured triangular meshes. The proposed PAMPA method use a globally continuous representation of the variables, with degree of freedoms (DoFs) consisting of point values on the edges and average values within each triangular element. The update of cell averages is carried out using a conservative form of the partial differential equations (PDEs), while the update of point values -- unconstrained by local conservation -- follows a non-conservative formulation. The powerful PAMPA framework offers great flexibility in the choice of variables for the non-conservative form, including conservative variables, primitive variables, and other possible sets of variables. In order to preserve a wider class of steady-state solutions, we introduce pressure-momentum-temperature variables instead of using the standard conservative or primitive ones. By utilizing these new variables and the associated non-conservative form, along with adopting suitable Gaussian quadrature rules in the discretization of conservative form, we prove that this new class of schemes is well-balanced for both ``lake at rest'' and isobaric steady states. We validate the performance of the proposed well-balanced PAMPA method through a series of numerical experiments, demonstrating their high-order accuracy, well-balancedness, and robustness.