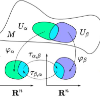
We generalize quasi-arithmetic means beyond scalars by considering the gradient map of a Legendre type real-valued function. The gradient map of a Legendre type function is proven strictly comonotone with a global inverse. It thus yields a generalization of strictly mononotone and differentiable functions generating scalar quasi-arithmetic means. Furthermore, the Legendre transformation gives rise to pairs of dual quasi-arithmetic averages via the convex duality. We study the invariance and equivariance properties under affine transformations of quasi-arithmetic averages via the lens of dually flat spaces of information geometry. We show how these quasi-arithmetic averages are used to express points on dual geodesics and sided barycenters in the dual affine coordinate systems. We then consider quasi-arithmetic mixtures and describe several parametric and non-parametric statistical models which are closed under the quasi-arithmetic mixture operation.
翻译:暂无翻译