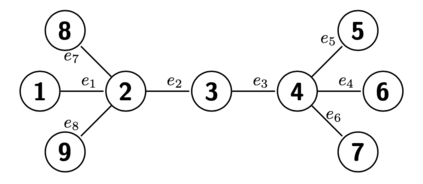
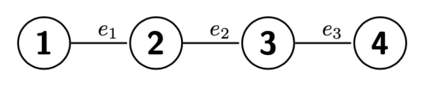
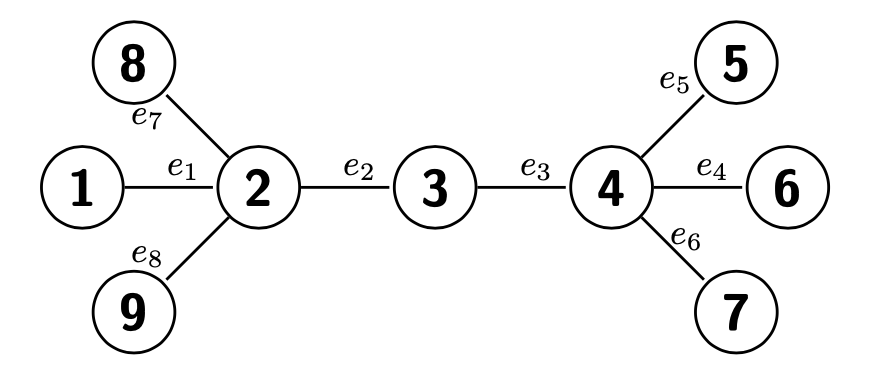
We present a geometrically enhanced Markov chain Monte Carlo sampler for networks based on a discrete curvature measure defined on graphs. Specifically, we incorporate the concept of graph Forman curvature into sampling procedures on both the nodes and edges of a network explicitly, via the transition probability of the Markov chain, as well as implicitly, via the target stationary distribution, which gives a novel, curved Markov chain Monte Carlo approach to learning networks. We show that integrating curvature into the sampler results in faster convergence to a wide range of network statistics demonstrated on deterministic networks drawn from real-world data.
翻译:具体地说,我们将Forman曲线图的概念明确纳入网络节点和边缘的取样程序,通过Markov链的过渡概率,以及通过目标固定分布,间接地纳入网络的取样程序,这为学习网络提供了一个新颖的、曲线曲线式的Markov链条Monte Carlo 方法。 我们表明,将曲线纳入取样器的结果是更快地与从现实世界数据中提取的确定性网络显示的广泛网络统计数据相融合。