Rollout Algorithms and Approximate Dynamic Programming for Bayesian Optimization and Sequential Estimation

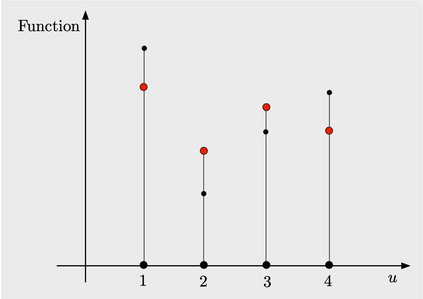
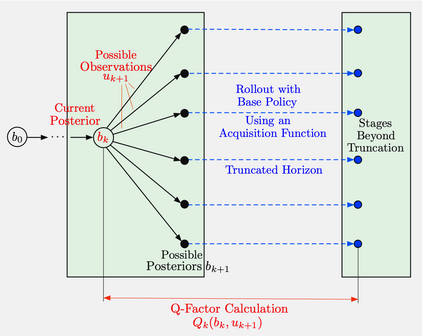
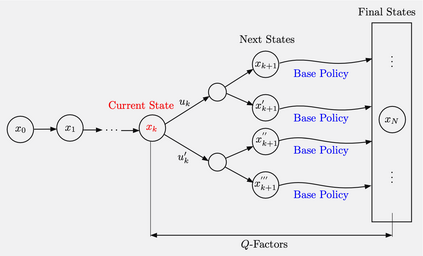
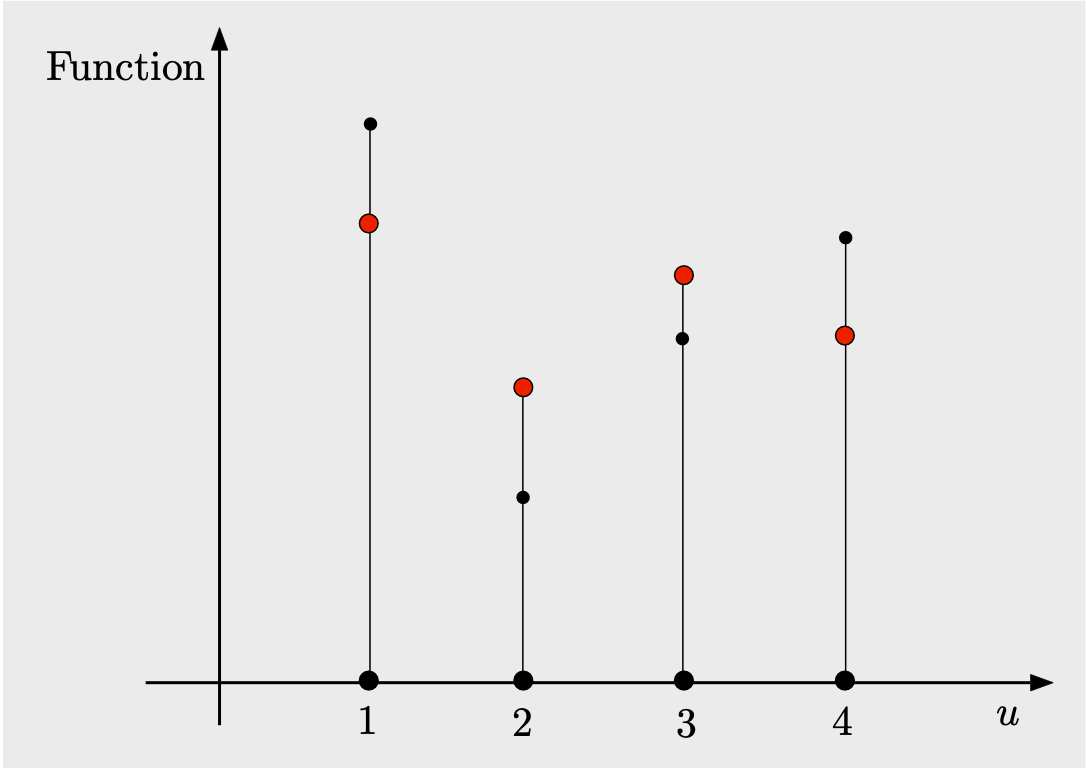
We provide a unifying approximate dynamic programming framework that applies to a broad variety of problems involving sequential estimation. We consider first the construction of surrogate cost functions for the purposes of optimization, and we focus on the special case of Bayesian optimization, using the rollout algorithm and some of its variations. We then discuss the more general case of sequential estimation of a random vector using optimal measurement selection, and its application to problems of stochastic and adaptive control. We finally consider related search and sequential decoding problems, and a rollout algorithm for the approximate solution of the Wordle and Mastermind puzzles, recently developed in the paper [BBB22].