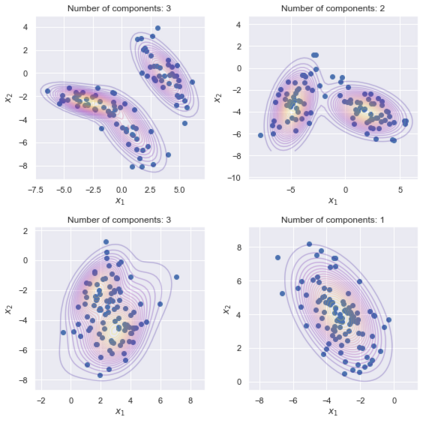
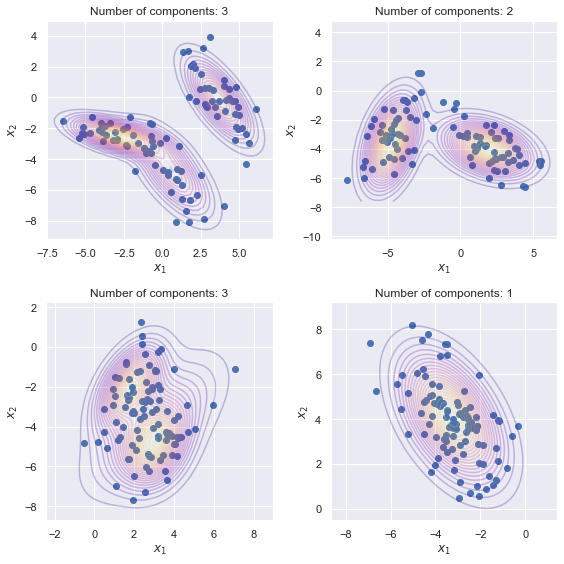
The problem of learning functions over spaces of probabilities - or distribution regression - is gaining significant interest in the machine learning community. A key challenge behind this problem is to identify a suitable representation capturing all relevant properties of the underlying functional mapping. A principled approach to distribution regression is provided by kernel mean embeddings, which lifts kernel-induced similarity on the input domain at the probability level. This strategy effectively tackles the two-stage sampling nature of the problem, enabling one to derive estimators with strong statistical guarantees, such as universal consistency and excess risk bounds. However, kernel mean embeddings implicitly hinge on the maximum mean discrepancy (MMD), a metric on probabilities, which may fail to capture key geometrical relations between distributions. In contrast, optimal transport (OT) metrics, are potentially more appealing, as documented by the recent literature on the topic. In this work, we propose the first OT-based estimator for distribution regression. We build on the Sliced Wasserstein distance to obtain an OT-based representation. We study the theoretical properties of a kernel ridge regression estimator based on such representation, for which we prove universal consistency and excess risk bounds. Preliminary experiments complement our theoretical findings by showing the effectiveness of the proposed approach and compare it with MMD-based estimators.
翻译:概率空间(或分布回归)的学习功能问题正引起机器学习界的极大兴趣。问题的关键挑战在于找到一种适当的代表方式,反映基本功能绘图的所有相关特性。分布回归由内核平均嵌入提供了原则性的方法,这提高了输入领域在概率水平上由内核引起的相似性。这一战略有效地解决了这一问题的两阶段抽样性质,使得人们能够得出具有强有力的统计保证的估算器,如普遍一致性和超重风险界限。然而,内核隐含地嵌入了最大平均值差异(MMD),这是概率的衡量标准,可能无法捕捉分布之间的主要几何关系。相比之下,最佳运输(OT)衡量标准可能更具吸引力,正如最近关于该主题的文献所记载的那样。在这项工作中,我们提出了第一个基于OT的分布回归估计仪。我们利用了Sliced Vasserstein的距离,以获得基于OT的代表性。我们研究了一种理论性的理论性特征,以显示我们所拟议的超重的正值分析结果。