Dichotomies for \#CSP on graphs that forbid a clique as a minor

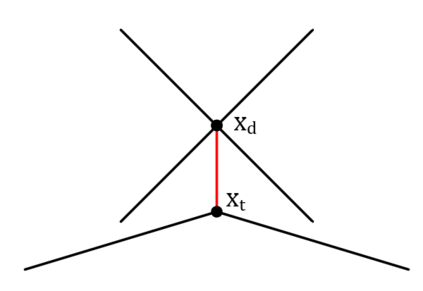
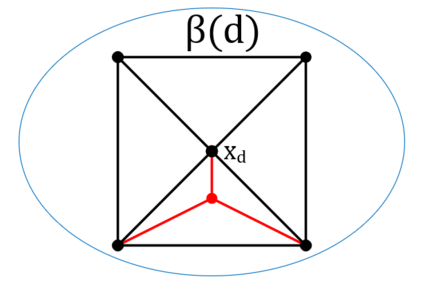
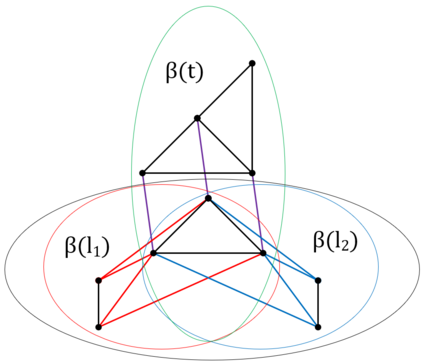
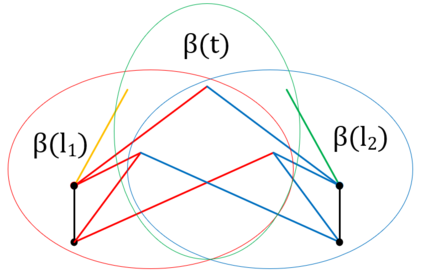
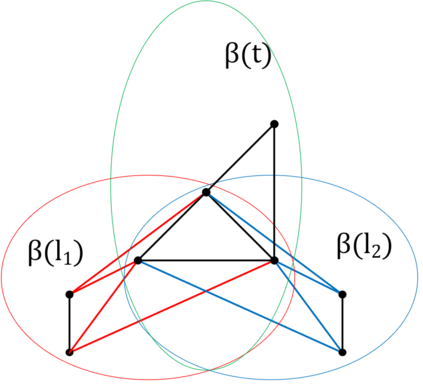
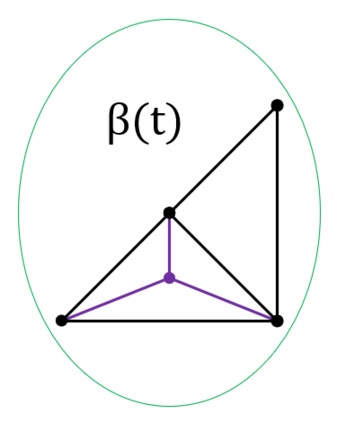
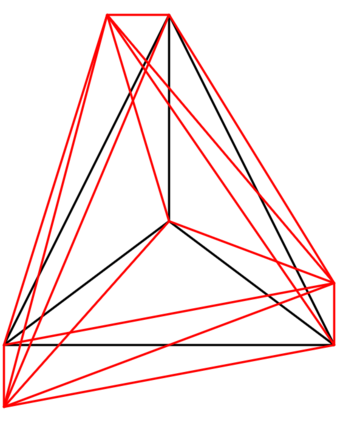
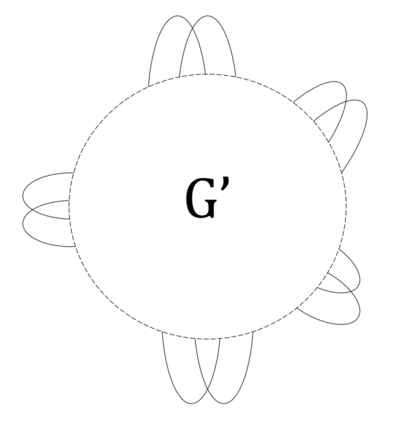
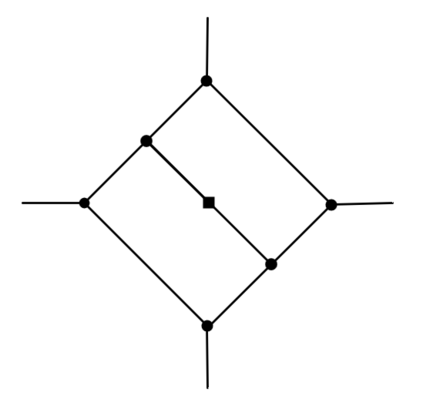
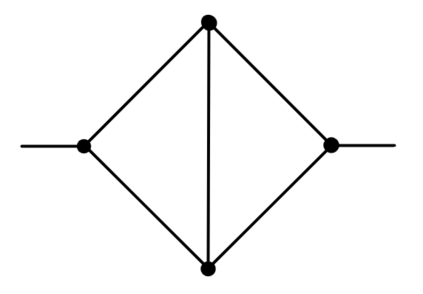
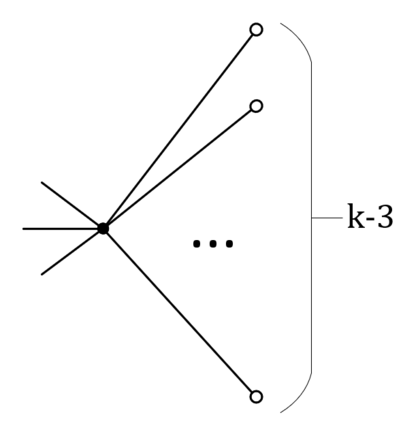
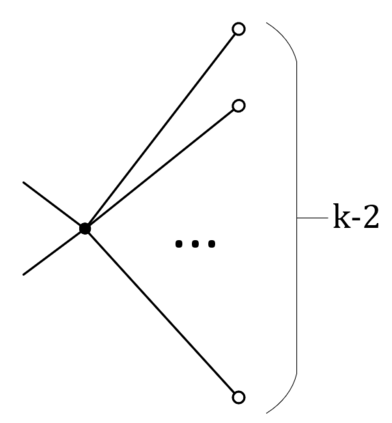
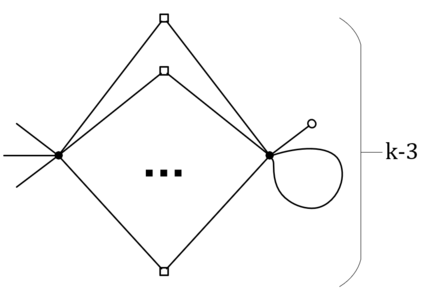
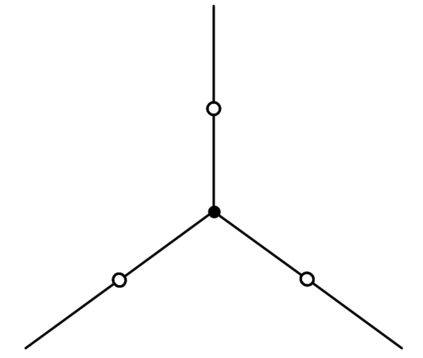
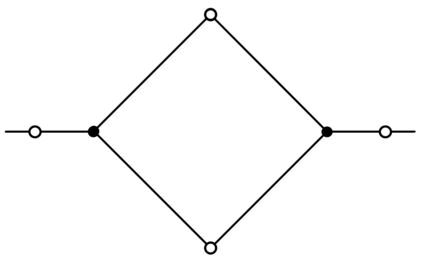
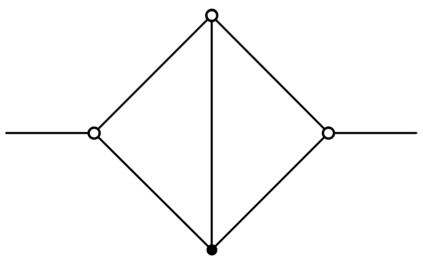
We prove complexity dichotomies for \#CSP problems (not necessarily symmetric) with Boolean domain and complex range on several typical minor-closed graph classes. These dichotomies give a complete characterization of the complexity of \#CSP on graph classes that forbid a complete graph as a minor. In particular, we also demonstrate that, whether the maximum degree of vertices is bounded may influence the complexity on specific minor-closed graph classes, and this phenomenon has never been observed in the previous related studies. Furthermore, our proofs integrate the properties of each graph class with the techniques from counting complexity, and develop a systematic approach for analyzing the complexity of \#CSP on these graph classes.