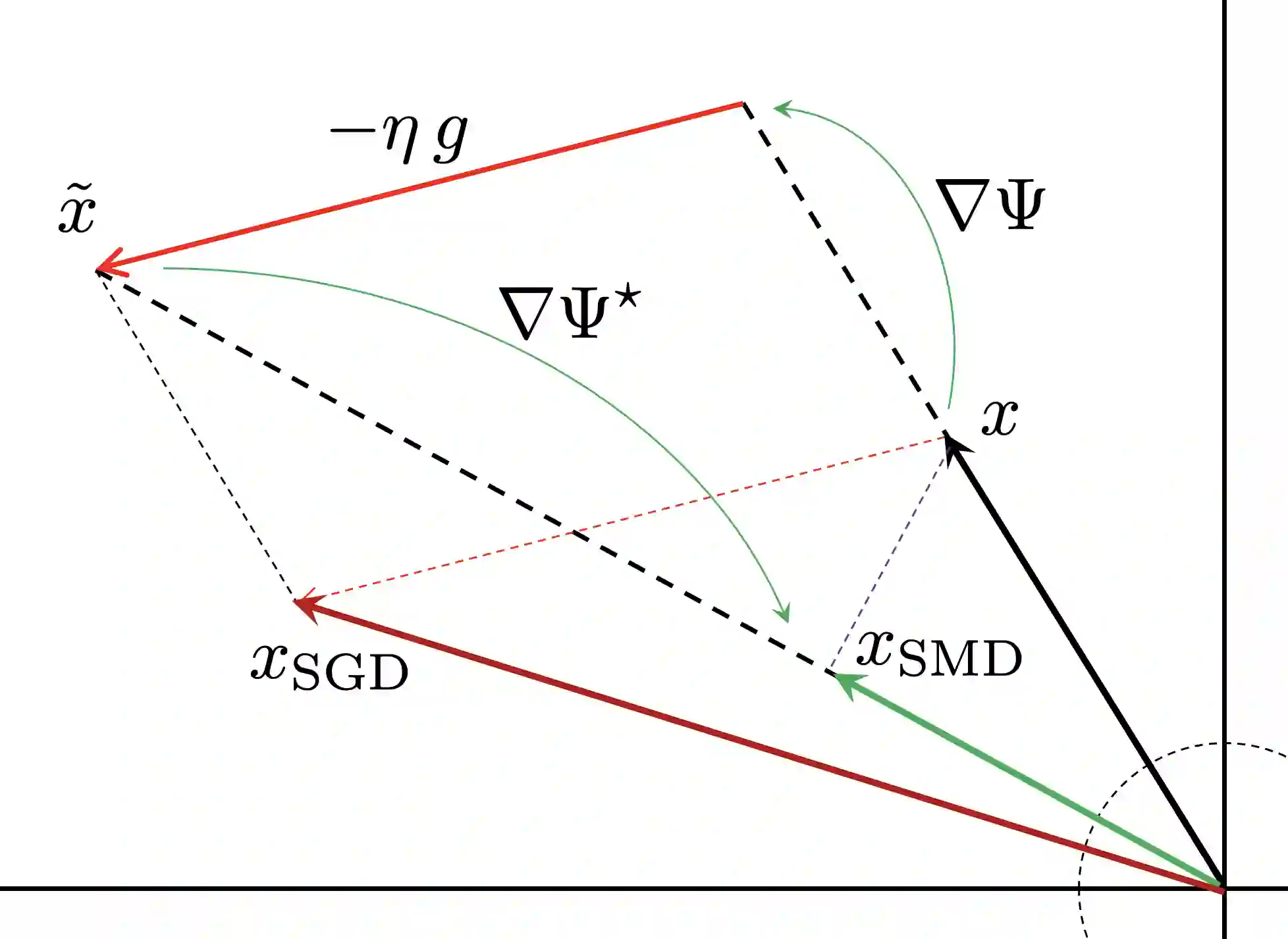
We study stochastic convex optimization under infinite noise variance. Specifically, when the stochastic gradient is unbiased and has uniformly bounded $(1+\kappa)$-th moment, for some $\kappa \in (0,1]$, we quantify the convergence rate of the Stochastic Mirror Descent algorithm with a particular class of uniformly convex mirror maps, in terms of the number of iterations, dimensionality and related geometric parameters of the optimization problem. Interestingly this algorithm does not require any explicit gradient clipping or normalization, which have been extensively used in several recent empirical and theoretical works. We complement our convergence results with information-theoretic lower bounds showing that no other algorithm using only stochastic first-order oracles can achieve improved rates. Our results have several interesting consequences for devising online/streaming stochastic approximation algorithms for problems arising in robust statistics and machine learning.
翻译:具体地说,当蒸汽梯度是公正的,并且统一约束$(1 ⁇ kappa) $1,1美元时,我们量化了“蒸汽镜底线算法”的趋同率,并用一个特定类别的统一共振镜面镜像图,根据优化问题的迭代数、维度和相关几何参数来计算。有趣的是,这一算法并不要求任何明确的梯度剪切法或正常化,这在最近的一些实验和理论著作中已被广泛使用。我们用信息理论下限来补充我们的趋同结果,显示仅使用随机第一阶或手的其他算法都无法达到改进的速率。我们的结果对设计在线/流式随机直观算法,解决稳健的统计和机器学习中出现的问题,产生了一些有趣的后果。