One-dimensional Tensor Network Recovery

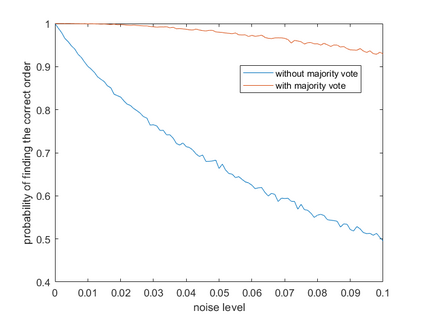
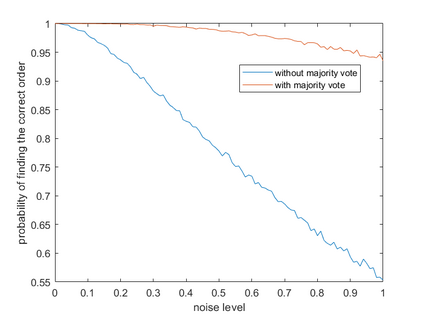
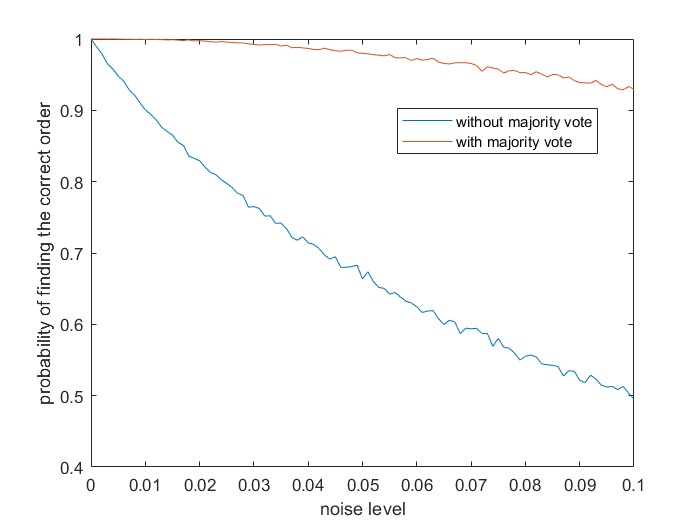
We study the recovery of the underlying graphs or permutations for tensors in tensor ring or tensor train format. Our proposed algorithms compare the matricization ranks after down-sampling, whose complexity is $O(d\log d)$ for $d$-th order tensors. We prove that our algorithms can almost surely recover the correct graph or permutation when tensor entries can be observed without noise. We further establish the robustness of our algorithms against observational noise. The theoretical results are validated by numerical experiments.