Symplectic Groupoids for Poisson Integrators

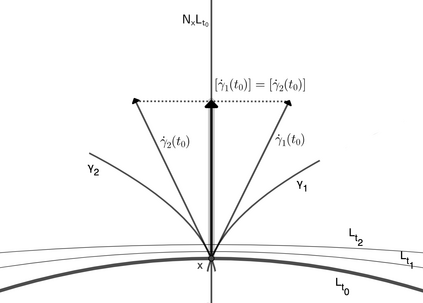
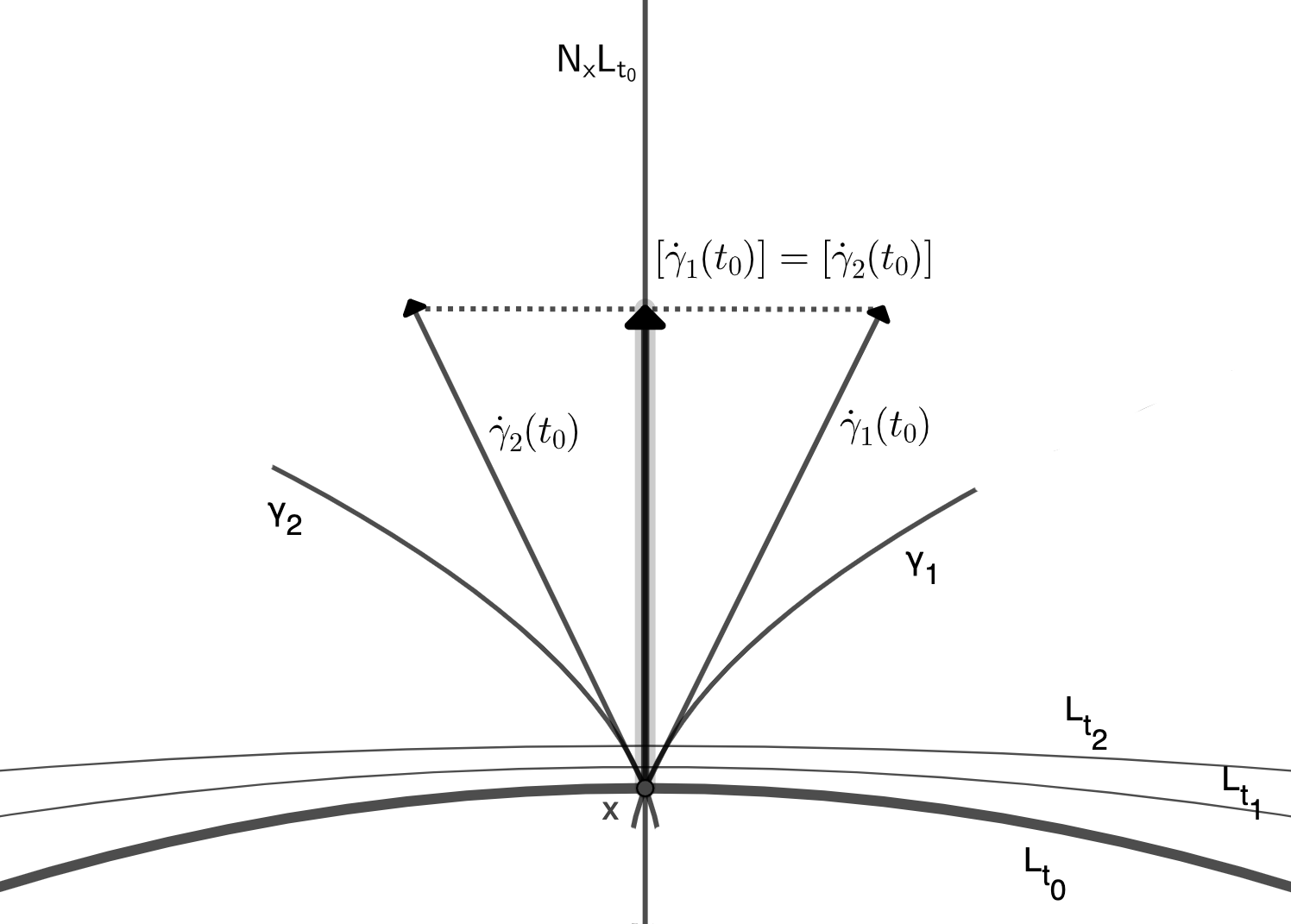
We use local symplectic Lie groupoids to construct Poisson integrators for generic Poisson structures. More precisely, recursively obtained solutions of a Hamilton-Jacobi-like equation are interpreted as Lagrangian bisections in a neighborhood of the unit manifold, that, in turn, give Poisson integrators. We also insist on the role of the Magnus formula, in the context of Poisson geometry, for the backward analysis of such integrators.