Auxiliary Functions as Koopman Observables: Data-Driven Polynomial Optimization for Dynamical Systems

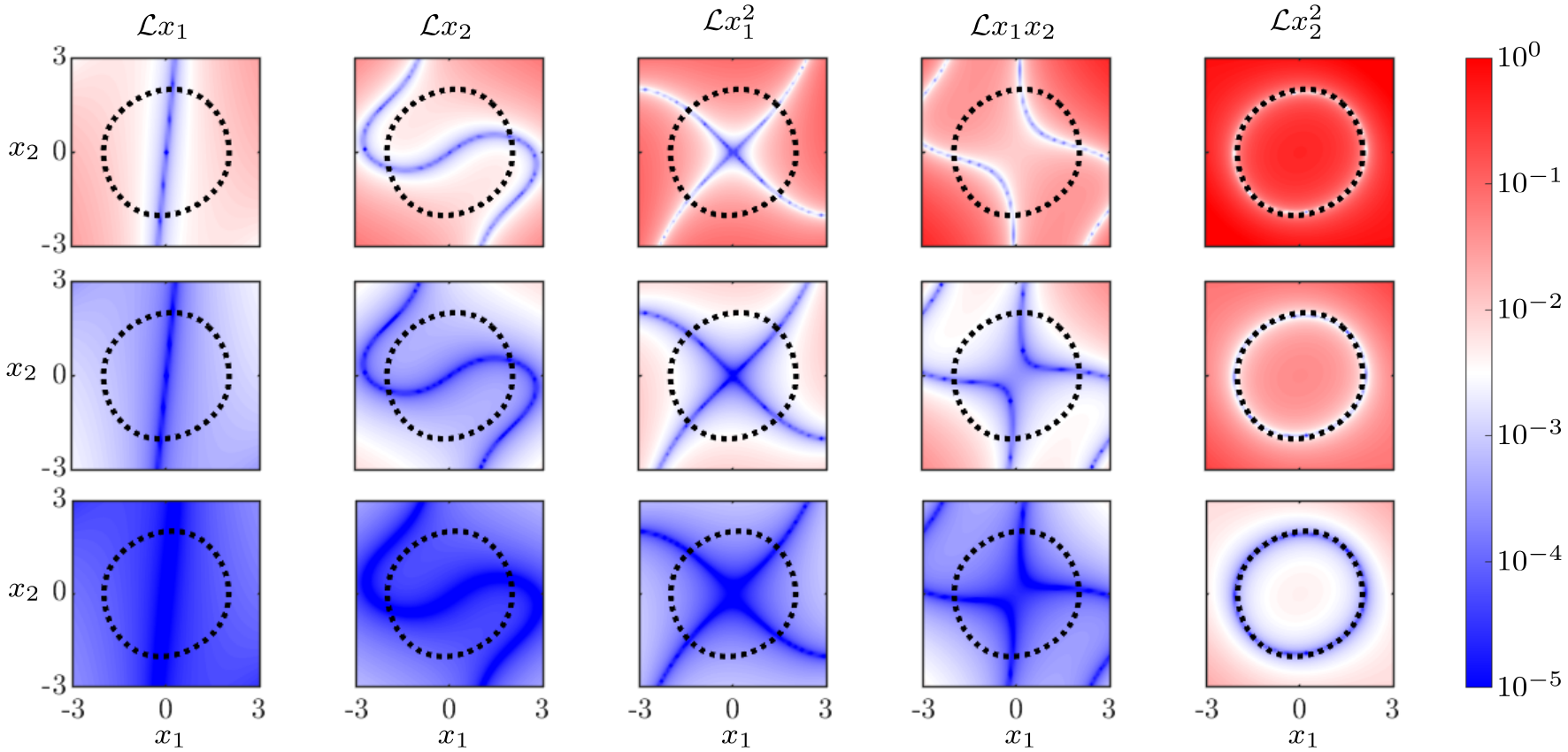
We present a flexible data-driven method for dynamical system analysis that does not require explicit model discovery. The method is rooted in well-established techniques for approximating the Koopman operator from data and is implemented as a semidefinite program that can be solved numerically. The method is agnostic of whether data is generated through a deterministic or stochastic process, so its implementation requires no prior adjustments by the user to accommodate these different scenarios. Rigorous convergence results justify the applicability of the method, while also extending and uniting similar results from across the literature. Examples on discovering Lyapunov functions and on performing ergodic optimization for both deterministic and stochastic dynamics exemplify these convergence results and demonstrate the performance of the method.