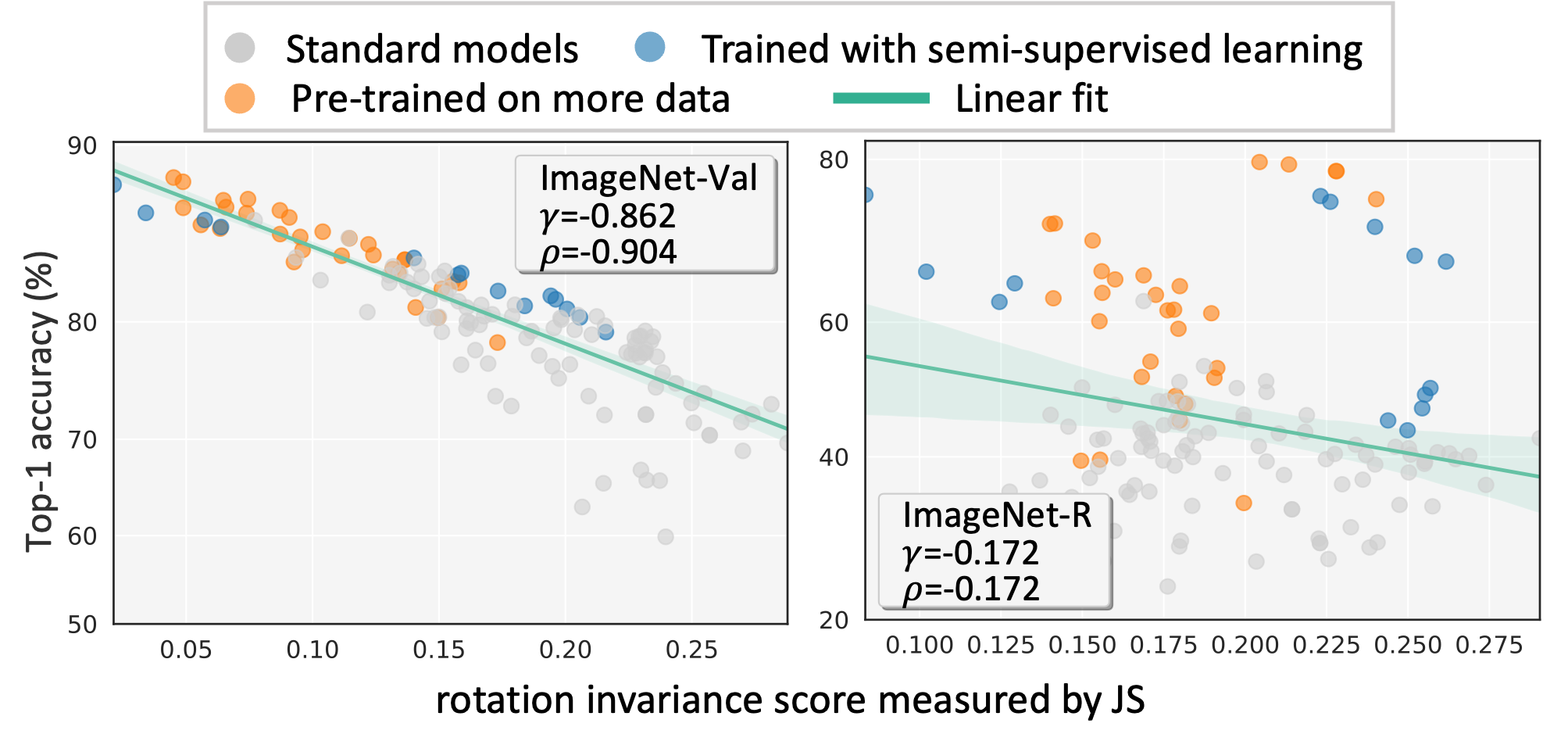
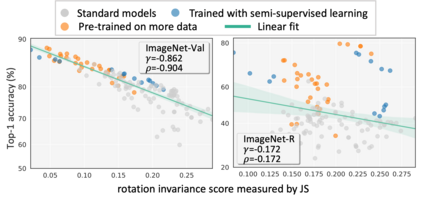
Generalization and invariance are two essential properties of any machine learning model. Generalization captures a model's ability to classify unseen data while invariance measures consistency of model predictions on transformations of the data. Existing research suggests a positive relationship: a model generalizing well should be invariant to certain visual factors. Building on this qualitative implication we make two contributions. First, we introduce effective invariance (EI), a simple and reasonable measure of model invariance which does not rely on image labels. Given predictions on a test image and its transformed version, EI measures how well the predictions agree and with what level of confidence. Second, using invariance scores computed by EI, we perform large-scale quantitative correlation studies between generalization and invariance, focusing on rotation and grayscale transformations. From a model-centric view, we observe generalization and invariance of different models exhibit a strong linear relationship, on both in-distribution and out-of-distribution datasets. From a dataset-centric view, we find a certain model's accuracy and invariance linearly correlated on different test sets. Apart from these major findings, other minor but interesting insights are also discussed.
翻译:通用化和易变是任何机器学习模式的两个基本特性。 通用化捕捉了模型对不可见数据进行分类的能力,而不变测量了数据转换模型预测的一致性。 现有研究表明了一种积极的关系: 典型的通用井应该是某些视觉因素的变异。 基于这种质量影响,我们做出了两种贡献。 首先, 我们引入了一种不依赖图像标签的简单合理的模型差异度(EI), 这是一种不依赖图像标签的简单合理的模型差异度量。 根据对测试图像及其变换版本的预测, EI测量了预测与信任度的一致程度。 其次, 使用EI计算的变异性分数, 我们进行了一个大型的定量相关性研究, 侧重于一般化和易变异性之间, 侧重于旋转和灰度变异。 从以模型为中心的观点来看, 我们观察不同模型的概括性和易变异性表现出强烈的线性关系, 在分布和分配外数据集上。 我们从一个数据集中心的角度, 我们发现某种模型的准确性和可变性直线性, 在不同的测试组中, 除了这些主要的洞察之外, 。