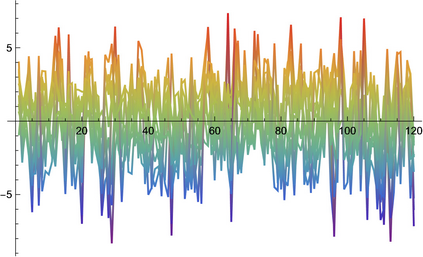
We consider the sparse principal component analysis for high-dimensional stationary processes. The standard principal component analysis performs poorly when the dimension of the process is large. We establish the oracle inequalities for penalized principal component estimators for the processes including heavy-tailed time series. The rate of convergence of the estimators is established. We also elucidate the theoretical rate for choosing the tuning parameter in penalized estimators. The performance of the sparse principal component analysis is demonstrated by numerical simulations. The utility of the sparse principal component analysis for time series data is exemplified by the application to average temperature data.
翻译:我们考虑的是高维固定过程的主要组成部分分析。当过程的层面巨大时,标准主要组成部分分析效果不佳。我们为包括重尾时间序列在内的过程的主要组成部分受罚估计人规定了甲骨文不平等。确定了估计人的趋同率。我们还阐明了在受罚估计人中选择调制参数的理论率。稀大主要组成部分分析的性能通过数字模拟得到证明。对平均温度数据应用了稀少主要组成部分分析对时间序列数据的效用,以平均温度数据为例证。