Flow-Based Integrated Assignment and Path-Finding for Mobile Robot Sorting Systems

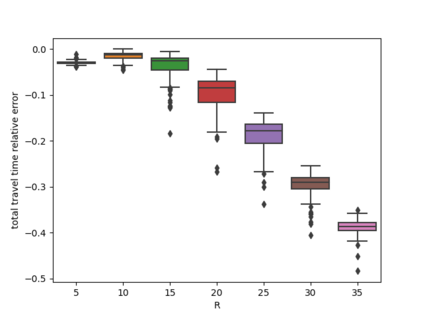
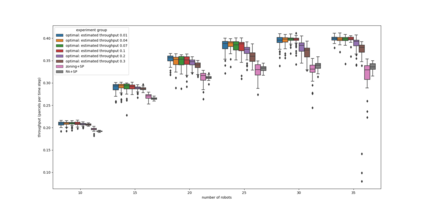
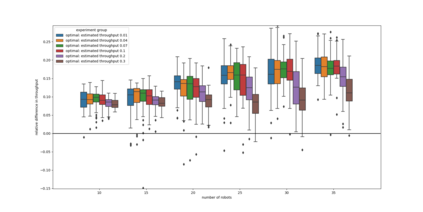
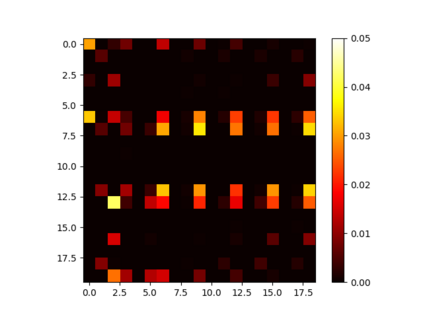
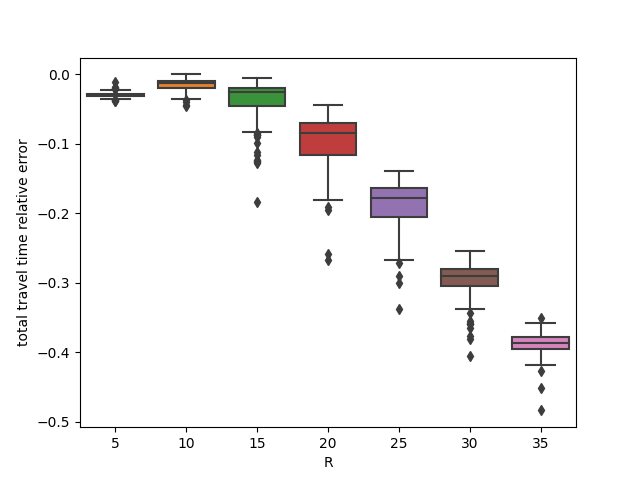
Express companies are deploying more robotic sorting systems, where mobile robots are used to sort incoming parcels by destination. In this study, we propose an integrated assignment and path-finding method for robots in such sorting systems. The method has two parts: offline and online. In the offline part, we represent the system as a traffic flow network, develop an approximate delay function using stochastic models, and solve the min-cost network flow problem. In the online part, robots are guided through the system according to the calculated optimal flow split probability. The online calculation of the method is decentralized and has linear complexity. Our method outperforms fast multi-agent path planning algorithms like prioritized planning because such algorithms lead to stochastic user equilibrium traffic assignment. In contrast, our method gives the approximated system-optimal traffic assignment. According to our simulations, our method can achieve 10%--20% higher throughput than zoning or random assignment. We also show that our method is robust even if the initial demand estimation is inaccurate.