Exploring Predictive States via Cantor Embeddings and Wasserstein Distance

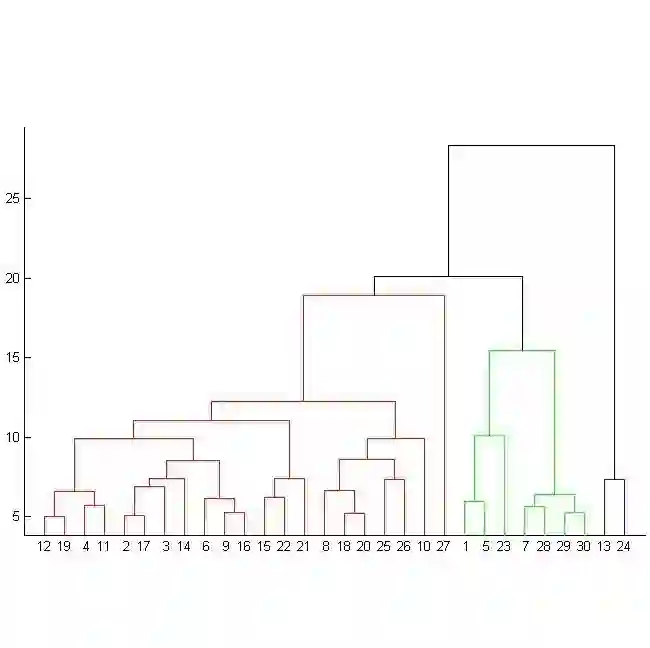
Predictive states for stochastic processes are a nonparametric and interpretable construct with relevance across a multitude of modeling paradigms. Recent progress on the self-supervised reconstruction of predictive states from time-series data focused on the use of reproducing kernel Hilbert spaces. Here, we examine how Wasserstein distances may be used to detect predictive equivalences in symbolic data. We compute Wasserstein distances between distributions over sequences ("predictions"), using a finite-dimensional embedding of sequences based on the Cantor for the underlying geometry. We show that exploratory data analysis using the resulting geometry via hierarchical clustering and dimension reduction provides insight into the temporal structure of processes ranging from the relatively simple (e.g., finite-state hidden Markov models) to the very complex (e.g., infinite-state indexed grammars).