An induction proof of the backpropagation algorithm in matrix notation

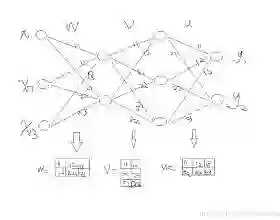
Backpropagation (BP) is a core component of the contemporary deep learning incarnation of neural networks. Briefly, BP is an algorithm that exploits the computational architecture of neural networks to efficiently evaluate the gradient of a cost function during neural network parameter optimization. The validity of BP rests on the application of a multivariate chain rule to the computational architecture of neural networks and their associated objective functions. Introductions to deep learning theory commonly present the computational architecture of neural networks in matrix form, but eschew a parallel formulation and justification of BP in the framework of matrix differential calculus. This entails several drawbacks for the theory and didactics of deep learning. In this work, we overcome these limitations by providing a full induction proof of the BP algorithm in matrix notation. Specifically, we situate the BP algorithm in the framework of matrix differential calculus, encompass affine-linear potential functions, prove the validity of the BP algorithm in inductive form, and exemplify the implementation of the matrix form BP algorithm in computer code.