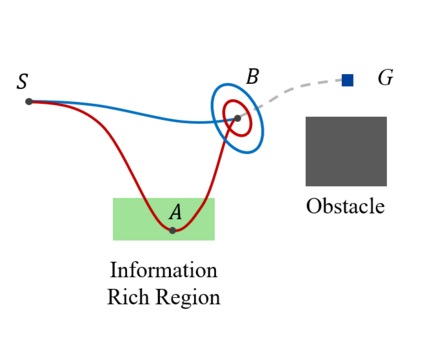
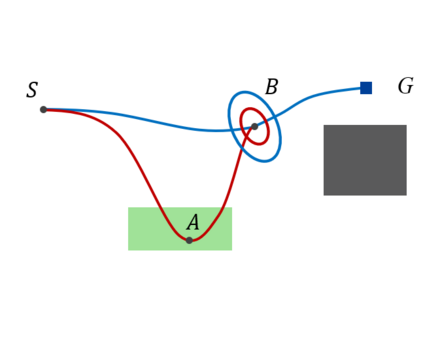
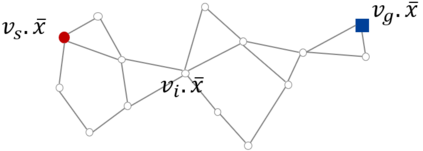
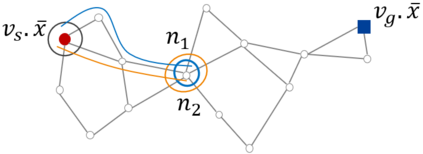
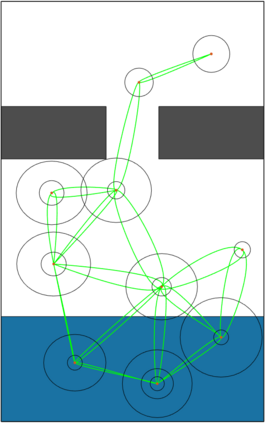
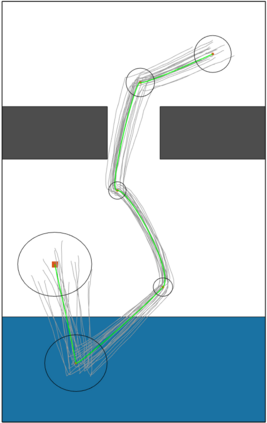
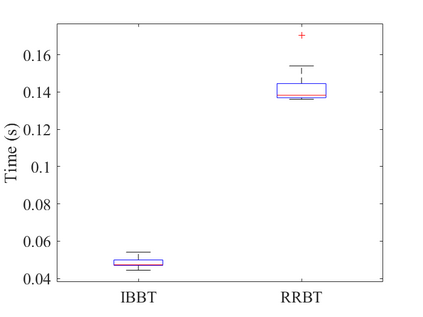
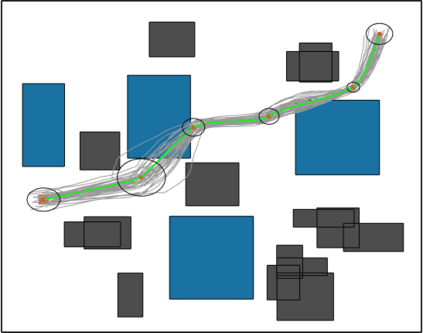
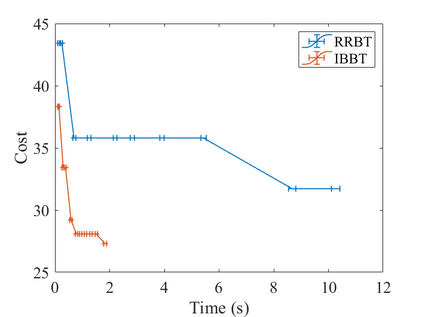
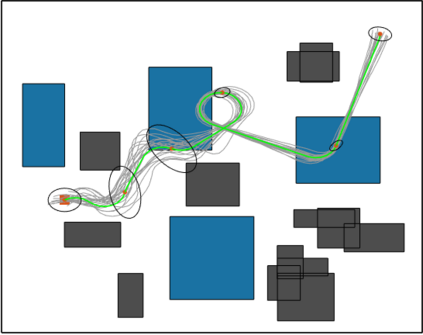
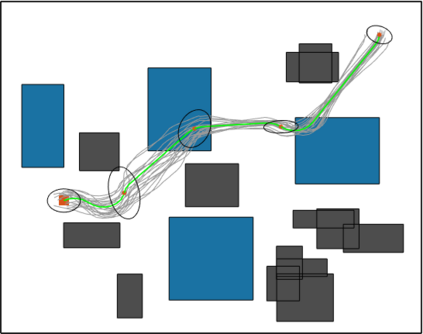
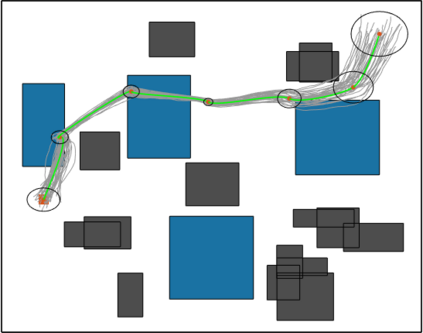
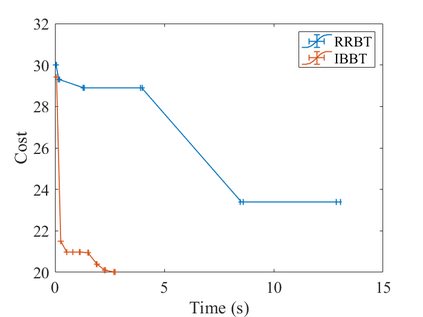
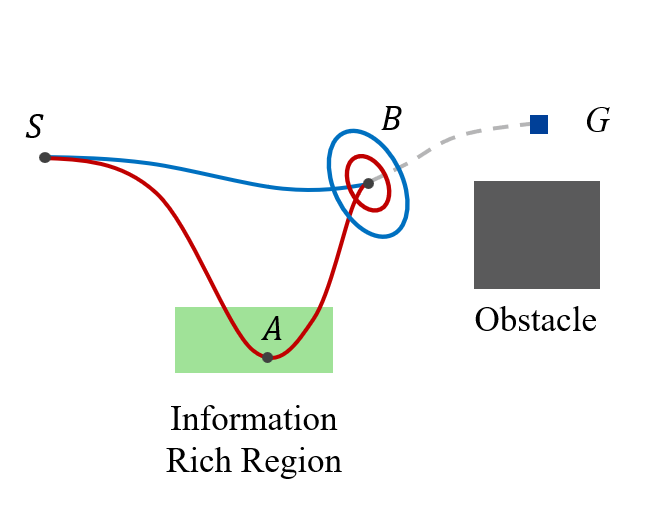
In this work, we propose the Informed Batch Belief Trees (IBBT) algorithm for motion planning under motion and sensing uncertainties. The original stochastic motion planning problem is divided into a deterministic motion planning problem and a graph search problem. We solve the deterministic planning problem using sampling-based methods such as PRM or RRG to construct a graph of nominal trajectories. Then, an informed cost-to-go heuristic for the original problem is computed based on the nominal trajectory graph. Finally, we grow a belief tree by searching over the graph using the proposed heuristic. IBBT interleaves between batch state sampling, nominal trajectory graph construction, heuristic computing, and search over the graph to find belief space motion plans. IBBT is an anytime, incremental algorithm. With an increasing number of batches of samples added to the graph, the algorithm finds motion plans that converge to the optimal one. IBBT is efficient by reusing results between sequential iterations. The belief tree searching is an ordered search guided by an informed heuristic. We test IBBT in different planning environments. Our numerical investigation confirms that IBBT finds non-trivial motion plans and is faster compared with previous similar methods.
翻译:在此工作中,我们提出了Informed Batch Belief Trees(IBBT)算法,用于不确定性下的运动规划。原始的随机运动规划问题被分成一个确定性运动规划问题和一个图搜索问题。我们使用基于采样的方法(如PRM或RRG)解决确定性规划问题,以构建标准轨迹的图。然后,基于标准轨迹图,计算原始问题的基于成本的启发式函数。最后,通过使用所提出的启发式函数在图上搜索来增长信念树。IBBT在批量状态采样、标准轨迹图构造、启发式计算和图搜索之间交替,以找到信念空间运动计划。IBBT是一个增量算法,逐渐加入采样批次数量时,算法会找到收敛于优化方案的运动计划。IBBT通过在顺序迭代之间重复使用结果而具有效率。信念树搜索是一种有序搜索,由一个基于启发式的指引。我们在不同的规划环境中测试了IBBT。我们的数值研究证实,与之前的类似方法相比,IBBT能够找到非平凡运动计划,并且速度更快。