Physics-Informed Model-Based Reinforcement Learning

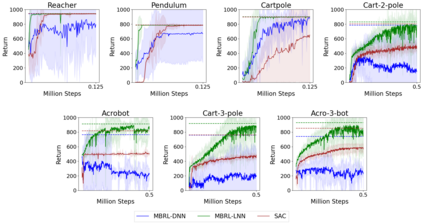
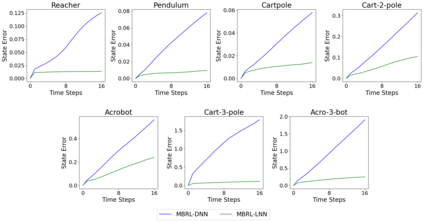
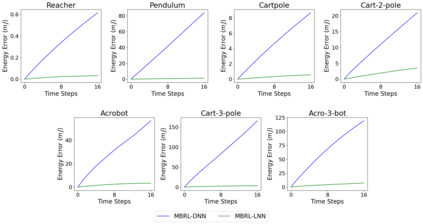
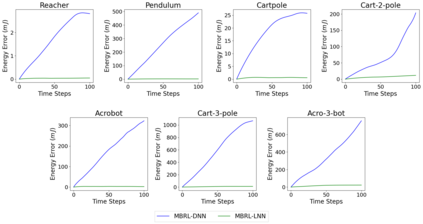
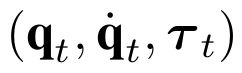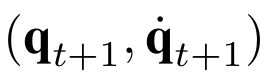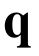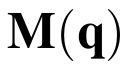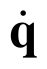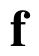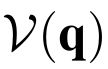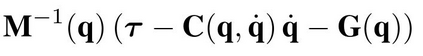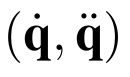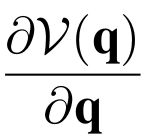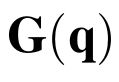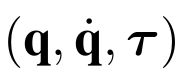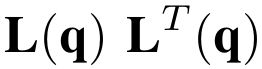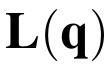One of the drawbacks of traditional reinforcement learning (RL) algorithms has been their poor sample efficiency. One approach to improve the sample efficiency is model-based RL. In our model-based RL algorithm, we learn a model of the environment, essentially its transition dynamics and reward function, use it to generate imaginary trajectories and backpropagate through them to update the policy, exploiting the differentiability of the model. Intuitively, learning more accurate models should lead to better performance. We focus on robotic systems undergoing rigid body motion without contacts. Recently, there has been growing interest in developing better deep neural network based dynamics models for physical systems, through better inductive biases. We compare two versions of our model-based RL algorithm, one which uses a standard deep neural network based dynamics model and the other which uses a much more accurate, physics-informed neural network based dynamics model. We show that, in model-based RL, model accuracy mainly matters in environments that are sensitive to initial conditions. In these environments, the physics-informed version of our algorithm achieves significantly better average-return and sample efficiency. In environments that are not sensitive to initial conditions, both versions of our algorithm achieve similar average-return, while the physics-informed version achieves better sample efficiency. We measure the sensitivity to initial conditions using the finite-time maximal Lyapunov exponent. We also show that, in challenging environments, where we need a lot of samples to learn, physics-informed model-based RL can achieve better average-return than state-of-the-art model-free RL algorithms such as Soft Actor-Critic, by generating accurate imaginary data.