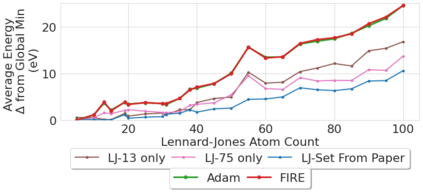
Optimization of non-convex loss surfaces containing many local minima remains a critical problem in a variety of domains, including operations research, informatics, and material design. Yet, current techniques either require extremely high iteration counts or a large number of random restarts for good performance. In this work, we propose adapting recent developments in meta-learning to these many-minima problems by learning the optimization algorithm for various loss landscapes. We focus on problems from atomic structural optimization--finding low energy configurations of many-atom systems--including widely studied models such as bimetallic clusters and disordered silicon. We find that our optimizer learns a 'hopping' behavior which enables efficient exploration and improves the rate of low energy minima discovery. Finally, our learned optimizers show promising generalization with efficiency gains on never before seen tasks (e.g. new elements or compositions). Code will be made available shortly.
翻译:优化含有许多本地微粒的非混凝土损耗表面仍然是许多领域的一个关键问题,包括作业研究、信息学和材料设计。然而,目前的技术要么需要极高的迭代计数,要么需要大量随机重现,才能很好地表现。在这项工作中,我们建议通过学习各种损失地貌的优化算法,使元化学习的最新发展适应这些众多的微小问题。我们侧重于许多原子系统的原子结构结构结构优化-探索的低能量配置-包括广泛研究的模型,如双金属集群和无序硅。我们发现,我们的优化者学会了“购物”行为,从而能够高效地探索并改进低能源微型发现的速度。最后,我们学到的优化者展示了有希望的普及性,其效率收益在前所未有的任务(例如新元素或组成)上将很快公布。