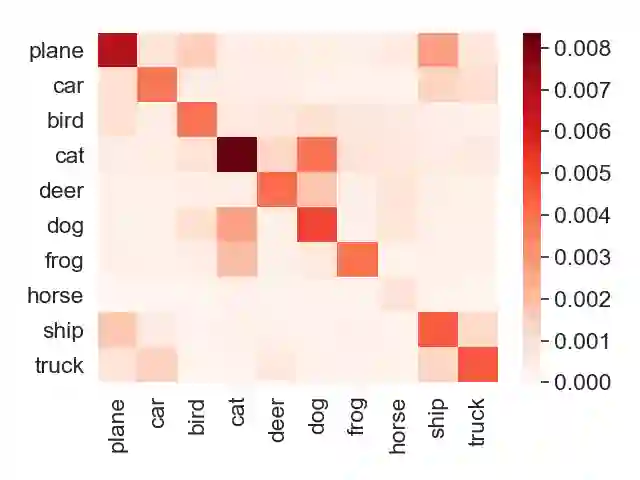
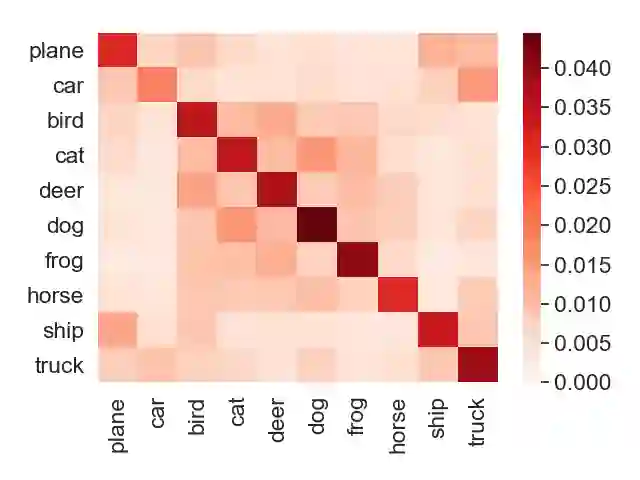
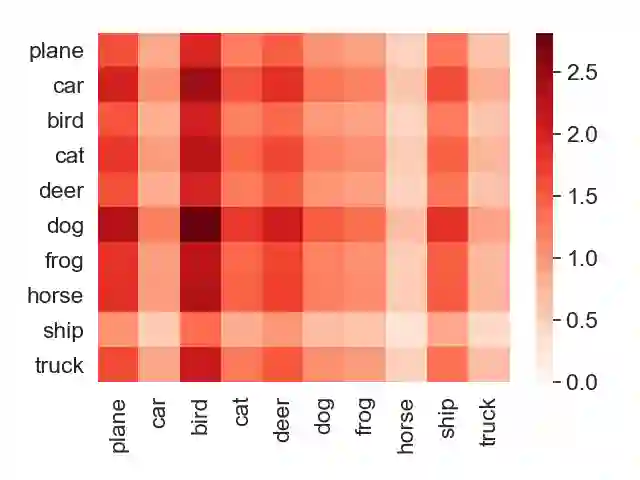
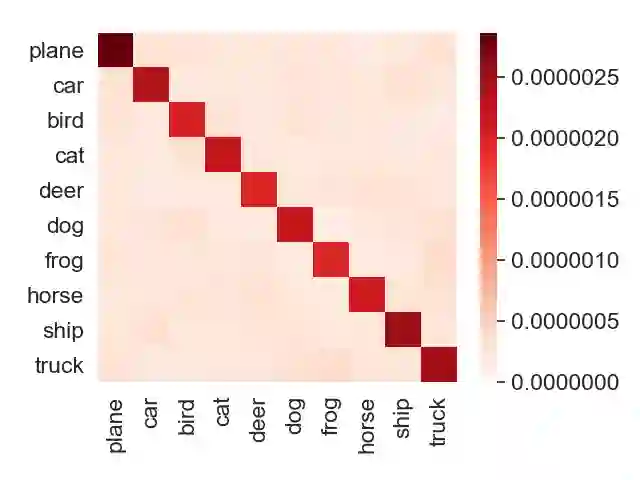
Algorithmic stability is a key characteristic to ensure the generalization ability of a learning algorithm. Among different notions of stability, \emph{uniform stability} is arguably the most popular one, which yields exponential generalization bounds. However, uniform stability only considers the worst-case loss change (or so-called sensitivity) by removing a single data point, which is distribution-independent and therefore undesirable. There are many cases that the worst-case sensitivity of the loss is much larger than the average sensitivity taken over the single data point that is removed, especially in some advanced models such as random feature models or neural networks. Many previous works try to mitigate the distribution independent issue by proposing weaker notions of stability, however, they either only yield polynomial bounds or the bounds derived do not vanish as sample size goes to infinity. Given that, we propose \emph{locally elastic stability} as a weaker and distribution-dependent stability notion, which still yields exponential generalization bounds. We further demonstrate that locally elastic stability implies tighter generalization bounds than those derived based on uniform stability in many situations by revisiting the examples of bounded support vector machines, regularized least square regressions, and stochastic gradient descent.
翻译:解析稳定性是确保学习算法普遍化能力的一个关键特征。 在不同的稳定性概念中, \ emph{ uniform stability} 可以说是最受欢迎的概念, 最受欢迎的概念可以产生指数化的概括性界限。 然而, 统一稳定性仅考虑最坏的损失变化( 或所谓的敏感度), 只需删除一个单一的数据点, 数据点是分布独立的, 因此是不可取的。 有许多例子显示, 损失的最坏情况敏感度远大于对被删除的单一数据点的平均敏感度, 特别是在一些先进的模型中, 如随机特征模型或神经网络 。 许多以前的工作试图通过提出较弱的稳定概念来缓解分配独立的问题, 但是, 它们可能只产生多度界限, 或衍生的界限不会随着样本大小变得无限而消失。 有鉴于此, 我们建议 \ emph{ 地方弹性稳定性概念仍然产生指数化的概括性概括性概括性界限。 我们进一步证明, 地方弹性稳定性意味着比基于许多局势中统一性稳定的结果更紧密的概括性, 通过重新审视定式的矢量级后级机, 支持固定式的定式的机级后级机。