Uniform Generalization Bounds for Overparameterized Neural Networks

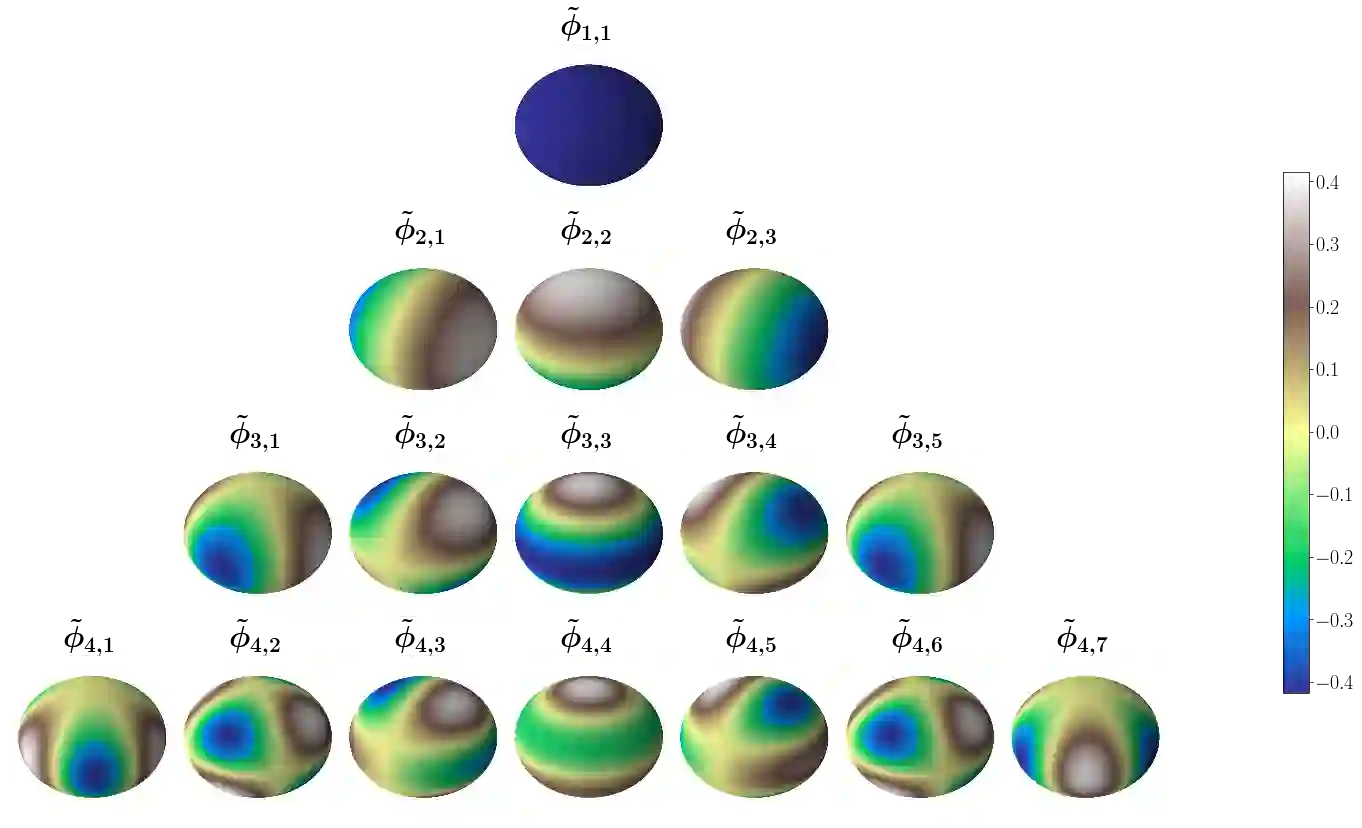
An interesting observation in artificial neural networks is their favorable generalization error despite typically being extremely overparameterized. It is well known that classical statistical learning methods often result in vacuous generalization errors in the case of overparameterized neural networks. Adopting the recently developed Neural Tangent (NT) kernel theory, we prove uniform generalization bounds for overparameterized neural networks in kernel regimes, when the true data generating model belongs to the reproducing kernel Hilbert space (RKHS) corresponding to the NT kernel. Importantly, our bounds capture the exact error rates depending on the differentiability of the activation functions. In order to establish these bounds, we propose the information gain of the NT kernel as a measure of complexity of the learning problem. Our analysis uses a Mercer decomposition of the NT kernel in the basis of spherical harmonics and the decay rate of the corresponding eigenvalues. As a byproduct of our results, we show the equivalence between the RKHS corresponding to the NT kernel and its counterpart corresponding to the Mat\'ern family of kernels, that induces a very general class of models. We further discuss the implications of our analysis for some recent results on the regret bounds for reinforcement learning algorithms, which use overparameterized neural networks.