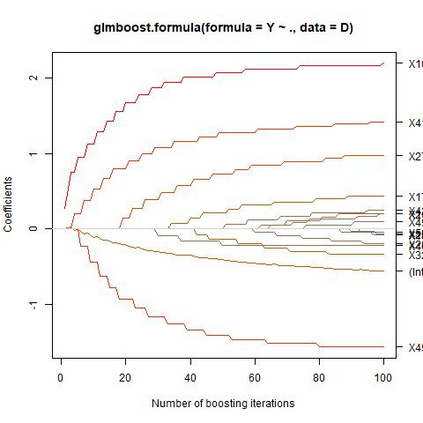
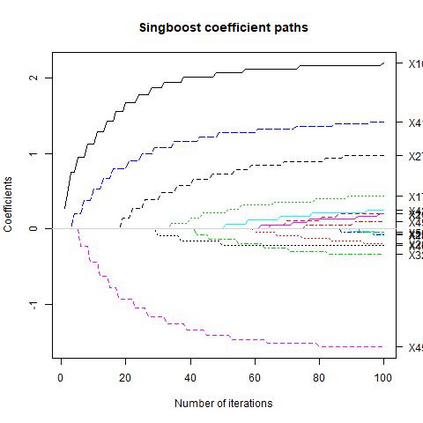
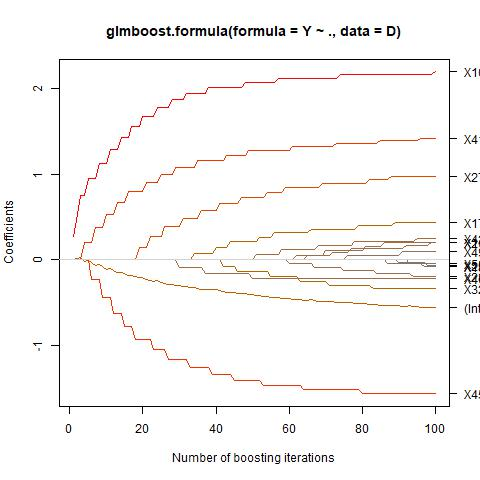
Sparse model selection by structural risk minimization leads to a set of a few predictors, ideally a subset of the true predictors. This selection clearly depends on the underlying loss function $\tilde L$. For linear regression with square loss, the particular (functional) Gradient Boosting variant $L_2-$Boosting excels for its computational efficiency even for very large predictor sets, while still providing suitable estimation consistency. For more general loss functions, functional gradients are not always easily accessible or, like in the case of continuous ranking, need not even exist. To close this gap, starting from column selection frequencies obtained from $L_2-$Boosting, we introduce a loss-dependent ''column measure'' $\nu^{(\tilde L)}$ which mathematically describes variable selection. The fact that certain variables relevant for a particular loss $\tilde L$ never get selected by $L_2-$Boosting is reflected by a respective singular part of $\nu^{(\tilde L)}$ w.r.t. $\nu^{(L_2)}$. With this concept at hand, it amounts to a suitable change of measure (accounting for singular parts) to make $L_2-$Boosting select variables according to a different loss $\tilde L$. As a consequence, this opens the bridge to applications of simulational techniques such as various resampling techniques, or rejection sampling, to achieve this change of measure in an algorithmic way.
翻译:以结构风险最小化方式选择的松散模型导致一组数个预测器, 最好是真实预测器的子集。 此选择显然取决于基本损失函数 $\ tilde L$。 对于带有平方损失的线性回归, 特定( 功能) 渐渐推式变换 $_ 2 $- $ boosting 优于其计算效率, 即使对于非常大的预测器组来说也是如此, 同时仍然提供合适的估算一致性 。 对于更一般的损失功能, 功能梯度并不总是容易获得, 或者像连续排序一样, 甚至根本不需要存在 。 要缩小这一差距, 从从从从$_ 2 $ 美元 boosting 获得的列选择频率开始, 我们引入一个基于损失的“ 校队量” $\\\\\\\ (\ tdel L) $ 美元 来计算变量选择 。 某些与特定损失 $\ title L$ 相关的变数从未被 $_ 2 美元选择 。 对于一般损失函数, 的单个部分反映 $\\\\\\\\ tanu_ r_ r_ r_ r_ lical ladeal a cal a cal deal a cal deal lection a lection a cal lection a colver lection a colver lection a coldection a cal lection a cal lection a cal lections a legdections lection a cal legal lections lection a lections a cal legycal leg) a cal a cal sictions a sictions a cal a fical sictions a sical sical a siction sical a sical sical sictional siction sictional sical sical sical sical sical sical sial sial sial sial sial sial sial sical sical sical sical sical sial sial