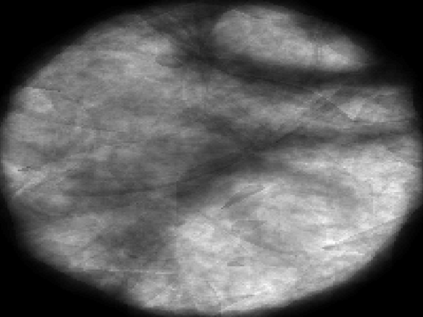
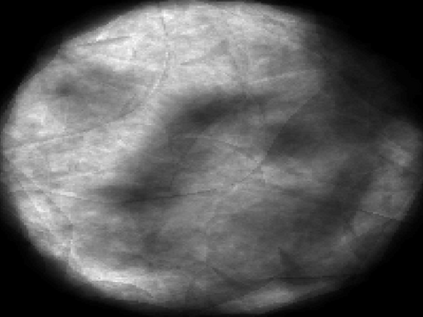
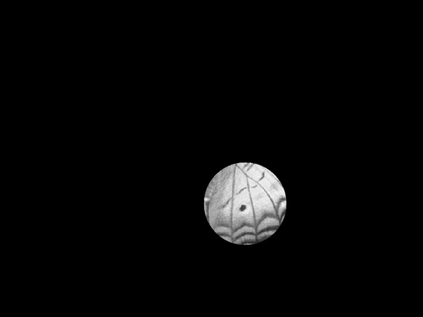
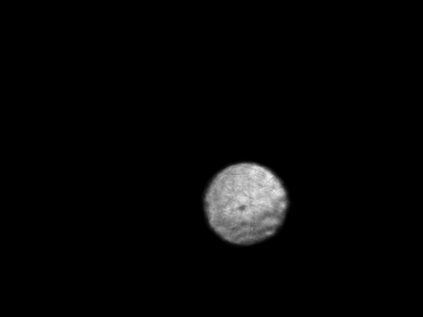
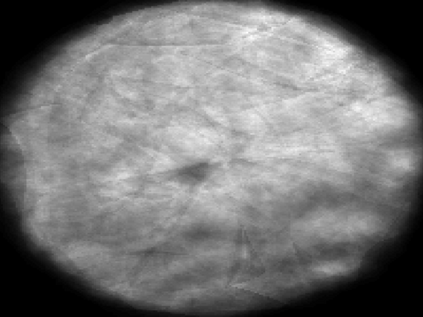
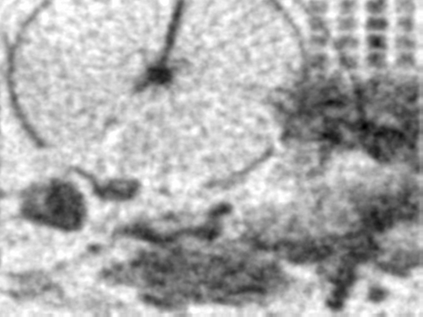
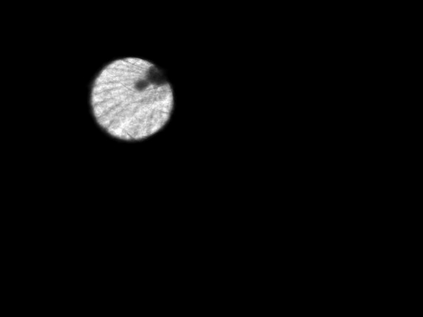
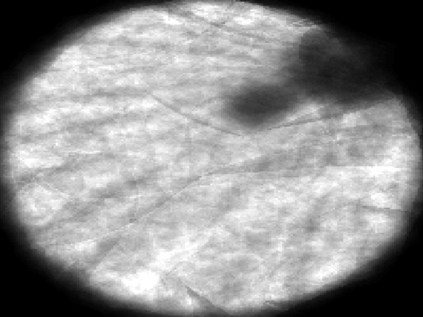
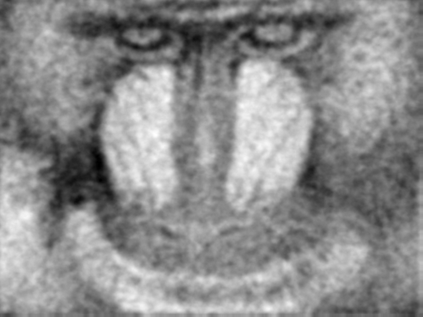
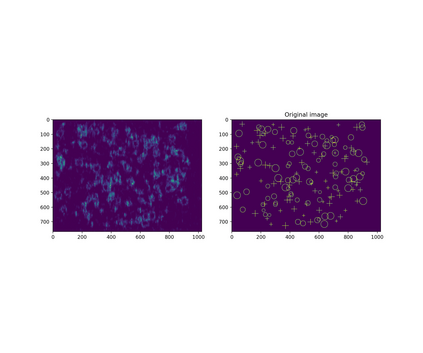
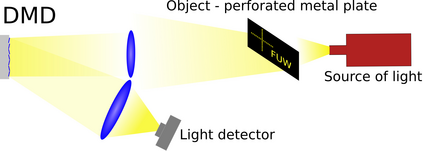
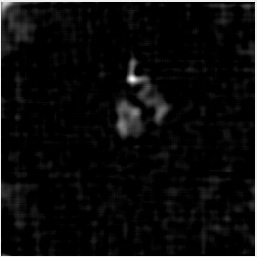
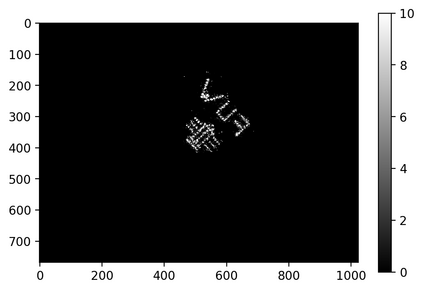
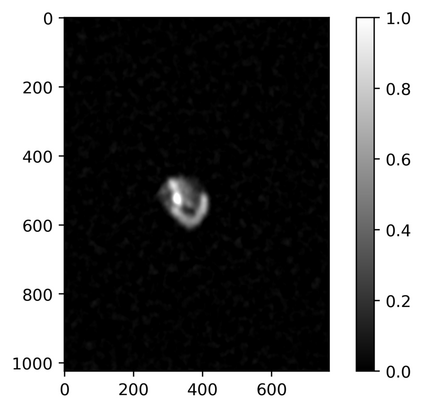
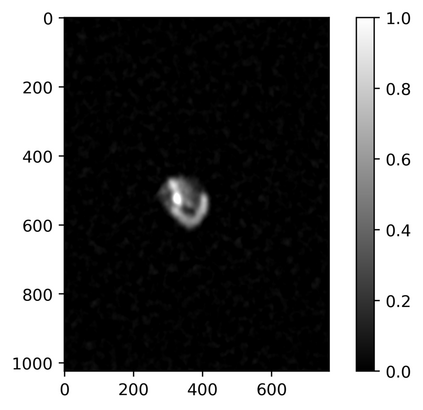
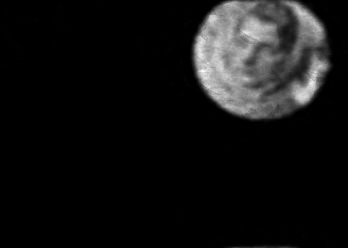
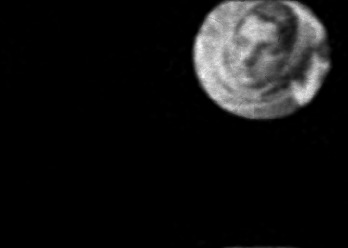
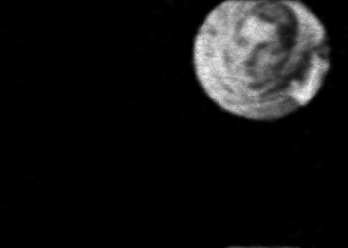
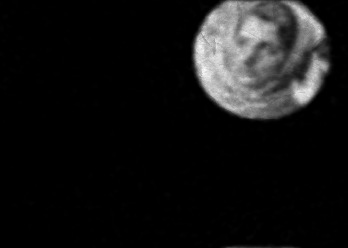
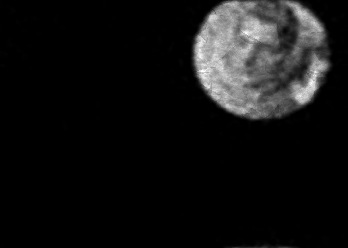
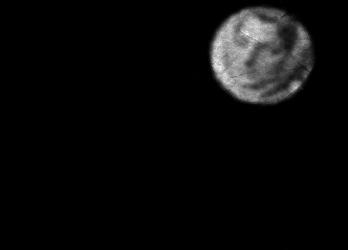
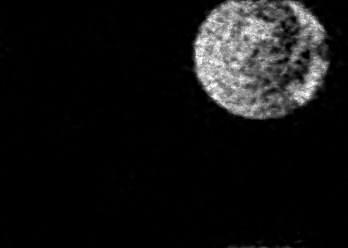
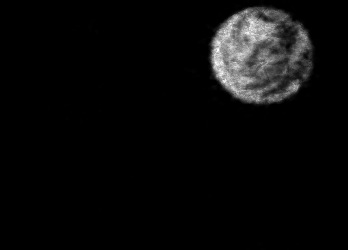
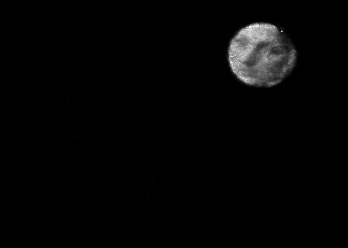
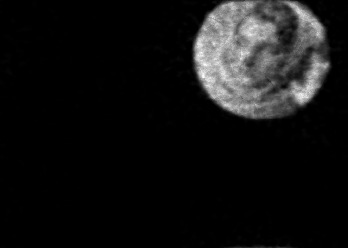
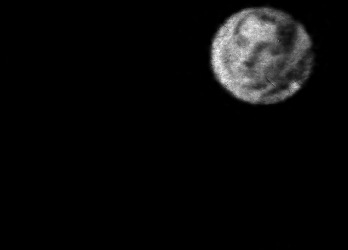
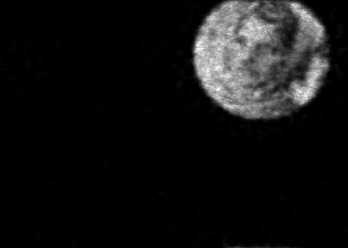
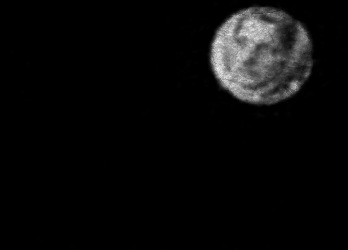
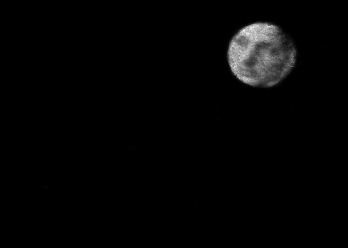
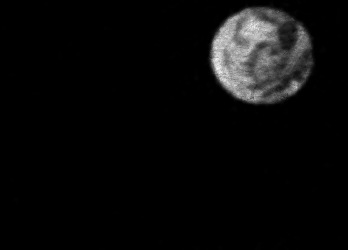
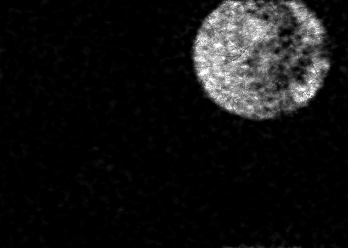
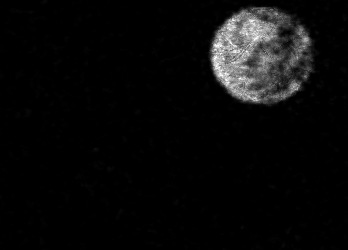
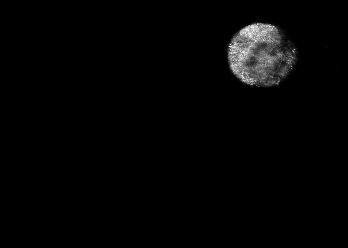
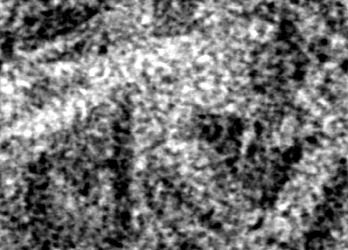
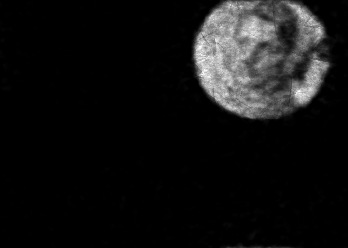
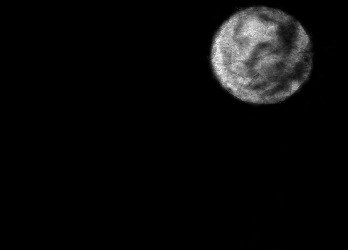
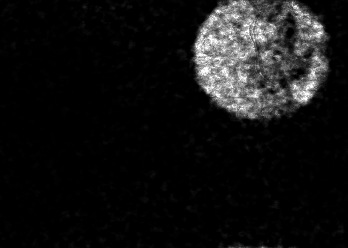
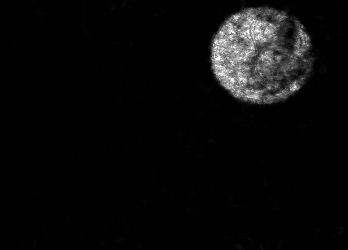
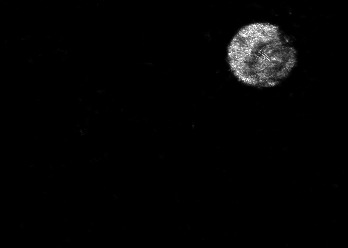
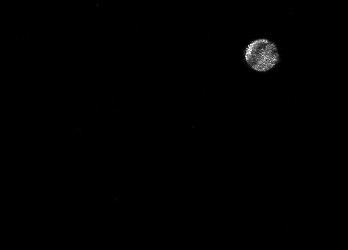
The usually reported pixel resolution of single pixel imaging (SPI) varies between $32 \times 32$ and $256 \times 256$ pixels falling far below imaging standards with classical methods. Low resolution results from the trade-off between the acceptable compression ratio, the limited DMD modulation frequency, and reasonable reconstruction time, and has not improved significantly during the decade of intensive research on SPI. In this paper we show that image measurement at the full resolution of the DMD, which lasts only a fraction of a second, is possible for sparse images or in a situation when the field of view is limited but is a priori unknown. We propose the sampling and reconstruction strategies that enable us to reconstruct sparse images at the resolution of $1024 \times 768$ within the time of $0.3~$s. Non-sparse images are reconstructed with less details. The compression ratio is on the order of $0.4 \%$ which corresponds to an acquisition frequency of $7~$Hz. Sampling is differential, binary, and non-adaptive, and includes information on multiple partitioning of the image which later allows us to determine the actual field of view. Reconstruction is based on the differential Fourier domain regularized inversion (D-FDRI). The proposed SPI framework is an alternative to both adaptive SPI, which is challenging to implement in real time, and to classical compressive sensing image recovery methods, which are very slow at high resolutions.
翻译:通常报告的单像素成像(STI)的像素解析度在32 32美元到256美元之间不等。 通常报告的单像素成像(SPI)的像素解解析度在32 32美元到256美元之间不等, 远低于古典方法的象素标准。 低解度来自可接受的压缩比例、有限的DMD调制频率和合理的重建时间之间的权衡,在对SPI进行深入研究的十年期间,没有显著改善。 在本文中,我们显示DMD完全解析的图像测量值为0.4 + 美元,这只维持一秒的一小部分,可以用于稀释图像,或者在视野有限但先天未知的情况下。 我们建议采样和重建战略,使我们能够在1024\ 时间为768美元分辨率的分辨率解析中重建稀少的图像,在0.3美元到合理的SPIFF框架的常规调整后,SPI的实地调整率为0.4+RI的恢复方式,在正常的调整中,在正常的调整中,在正常的调整框架的调整后,在正常的调整后,在正常的调整后,在SFDFD框架中,在正常的调整后,在正常的调整中,在正常的调整的调整后,这是的调整后,在正常的调整中,在正常的调整的调整的调整中,在正常的调整后,在正确的调整的调整后,在正常的调整。