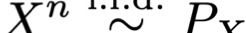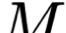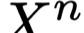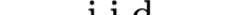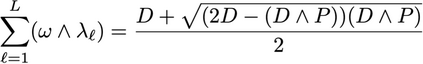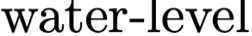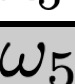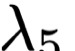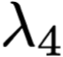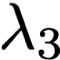We study the rate-distortion-perception (RDP) tradeoff for a memoryless source model in the asymptotic limit of large block-lengths. Our perception measure is based on a divergence between the distributions of the source and reconstruction sequences conditioned on the encoder output, which was first proposed in [1], [2]. We consider the case when there is no shared randomness between the encoder and the decoder. For the case of discrete memoryless sources we derive a single-letter characterization of the RDP function, thus settling a problem that remains open for the marginal metric introduced in Blau and Michaeli [3] (with no shared randomness). Our achievability scheme is based on lossy source coding with a posterior reference map proposed in [4]. For the case of continuous valued sources under squared error distortion measure and squared quadratic Wasserstein perception measure we also derive a single-letter characterization and show that a noise-adding mechanism at the decoder suffices to achieve the optimal representation. For the case of zero perception loss, we show that our characterization interestingly coincides with the results for the marginal metric derived in [5], [6] and again demonstrate that zero perception loss can be achieved with a $3$-dB penalty in the minimum distortion. Finally we specialize our results to the case of Gaussian sources. We derive the RDP function for vector Gaussian sources and propose a waterfilling type solution. We also partially characterize the RDP function for a mixture of vector Gaussians.
翻译:暂无翻译