Helicity-conservative Physics-informed Neural Network Model for Navier-Stokes Equations

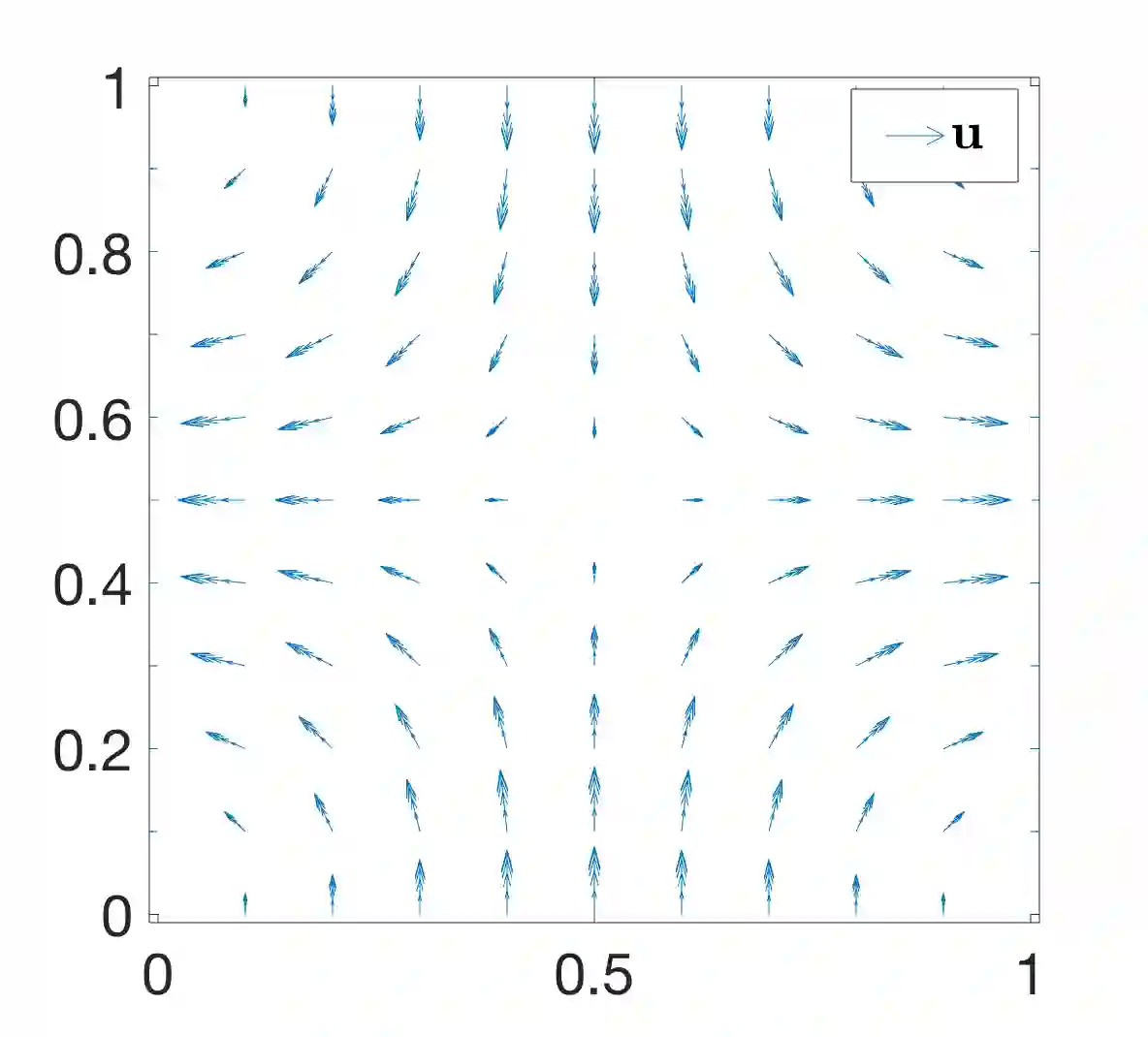
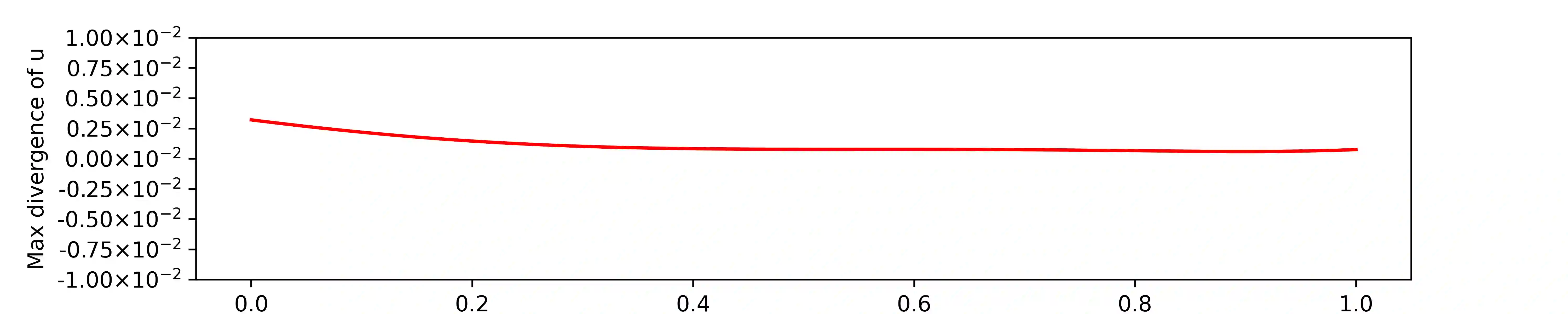
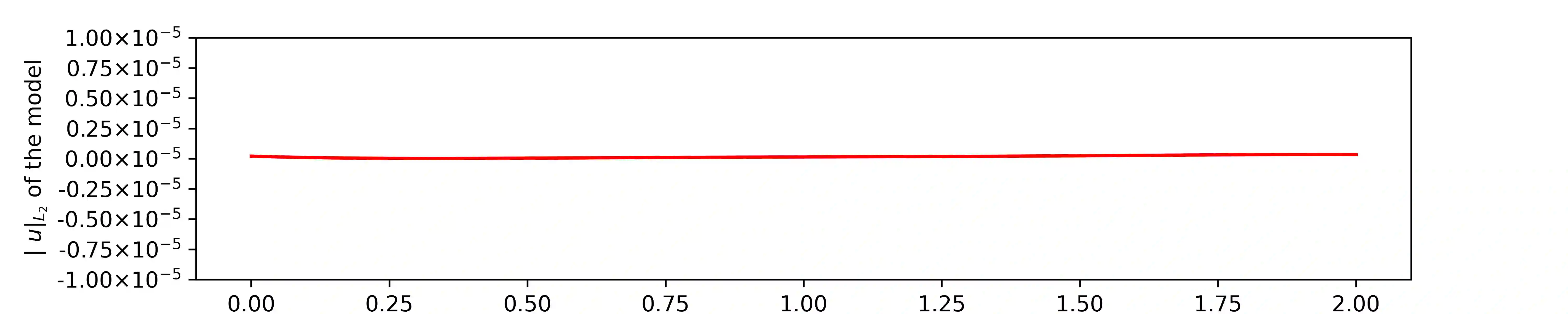
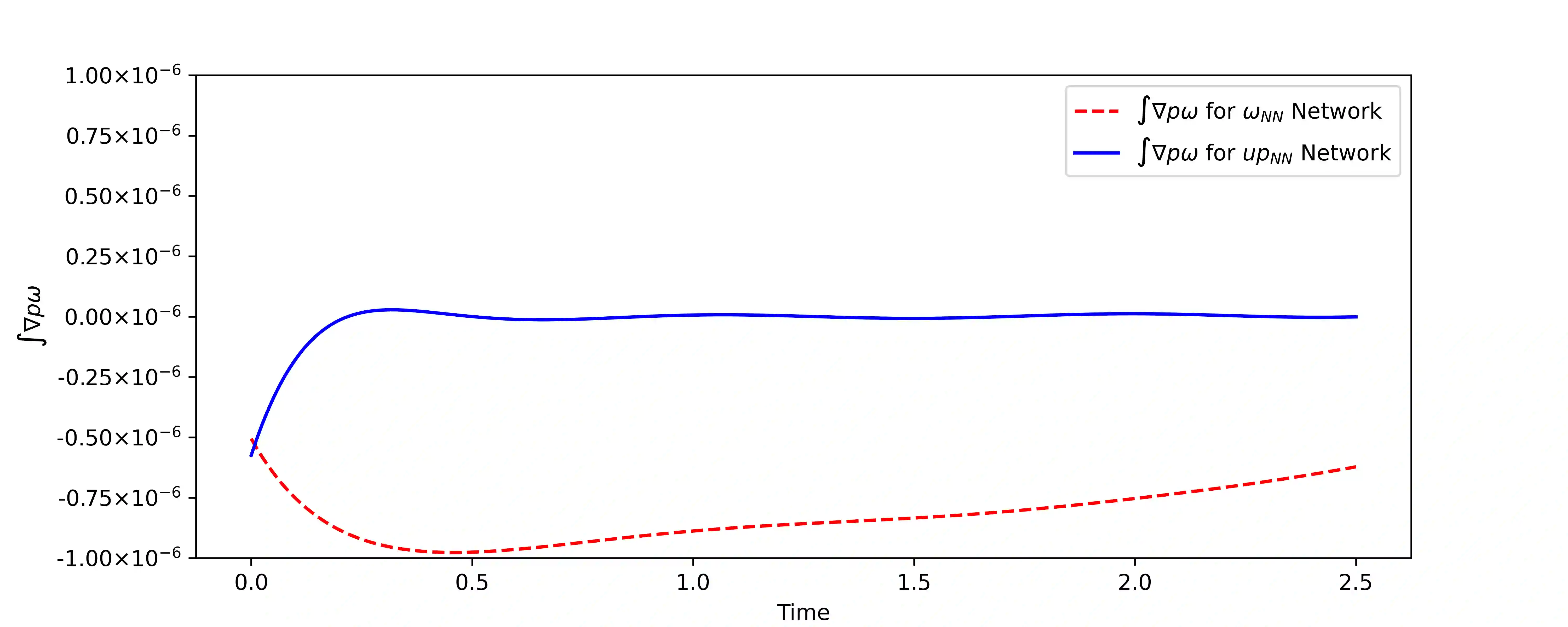
We design the helicity-conservative physics-informed neural network model for the Navier-Stokes equation in the ideal case. The key is to provide an appropriate PDE model as loss function so that its neural network solutions produce helicity conservation. Physics-informed neural network model is based on the strong form of PDE. We show that the relevant helicity-conservative finite element method based on the weak formulation of PDE can be somewhat different. More precisely, we compares the PINN formulation and the finite element method based on the weak formulation for conserving helicity and argues that for the conservation, strong PDE is more natural. Our result is justified by theory as well. Furthermore, a couple of numerical calculations are demonstrated to confirm our theoretical finding.