Nonparametric Bayesian inference for reversible multi-dimensional diffusions

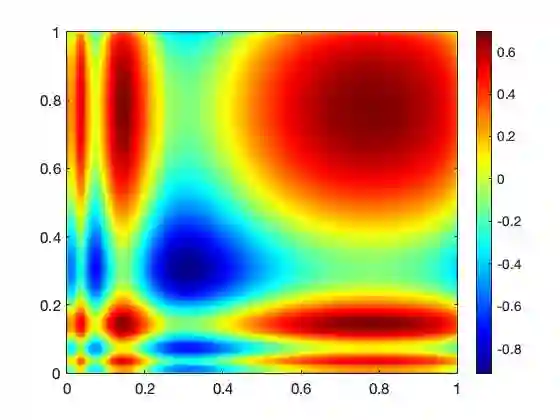
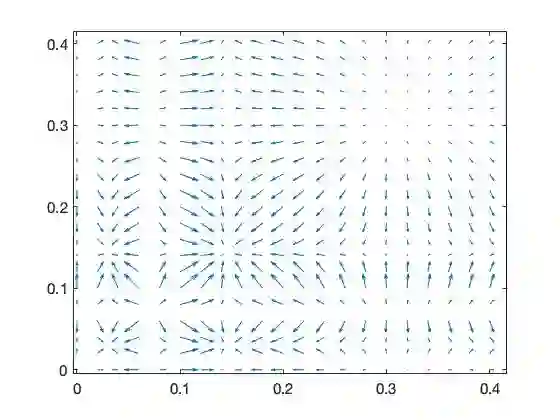
We study nonparametric Bayesian models for reversible multi-dimensional diffusions with periodic drift. For continuous observation paths, reversibility is exploited to prove a general posterior contraction rate theorem for the drift gradient vector field under approximation-theoretic conditions on the induced prior for the invariant measure. The general theorem is applied to Gaussian priors and $p$-exponential priors, which are shown to converge to the truth at the minimax optimal rate over Sobolev smoothness classes in any dimension