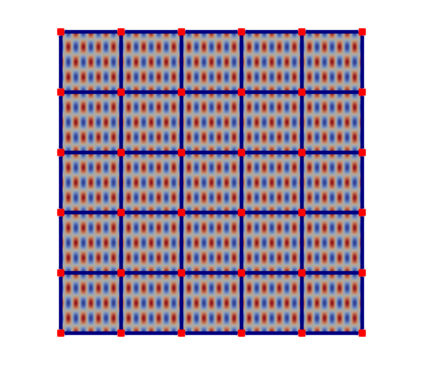
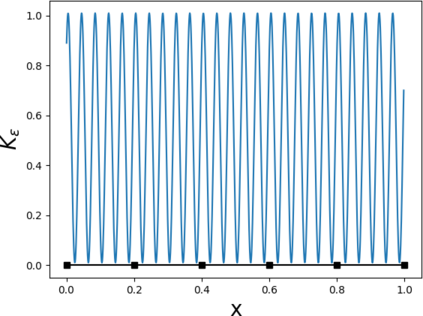
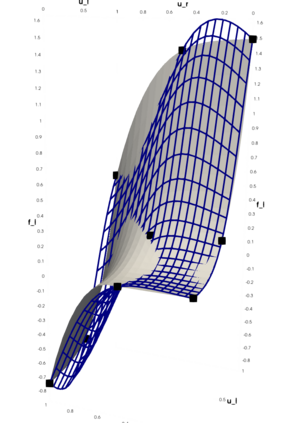
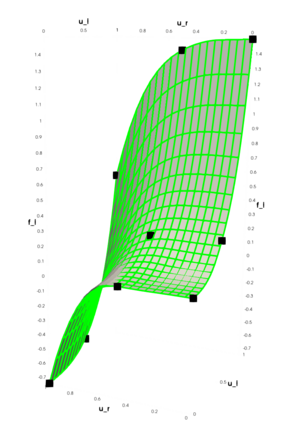
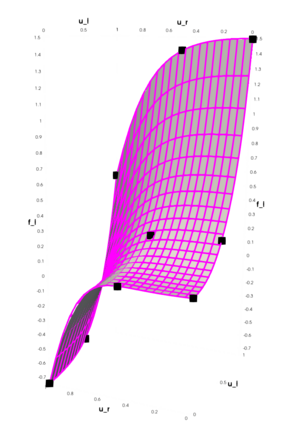
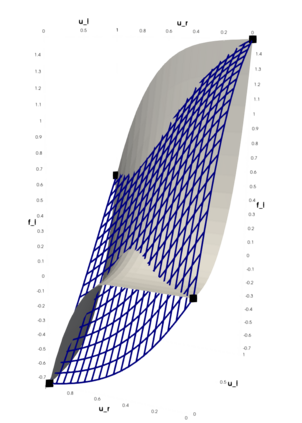
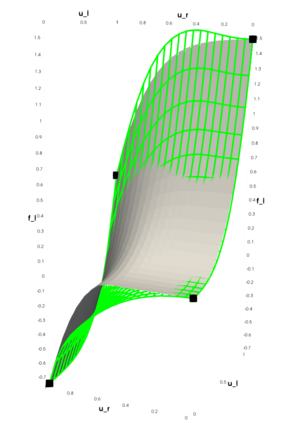
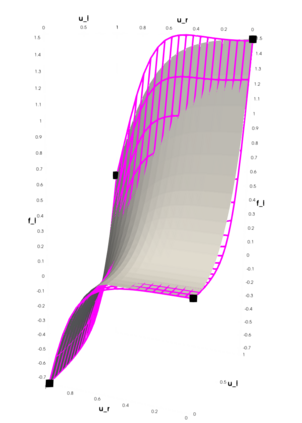
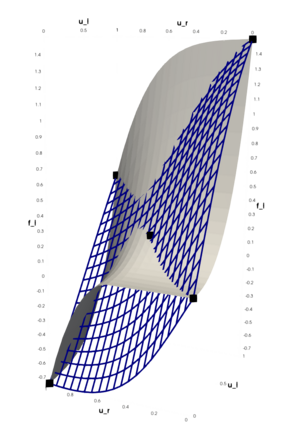
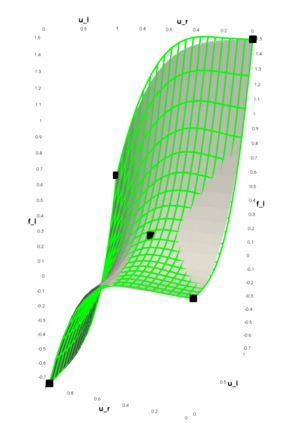
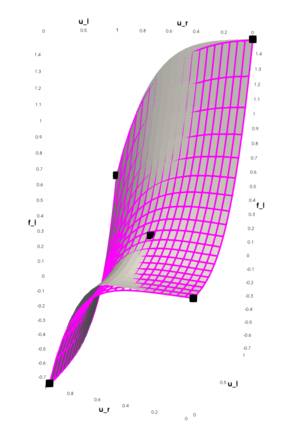
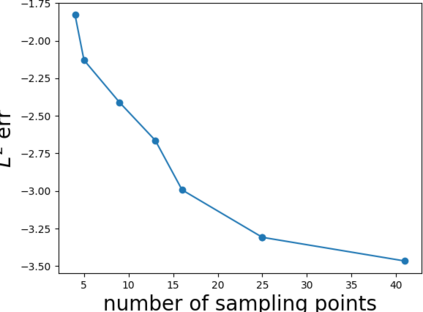
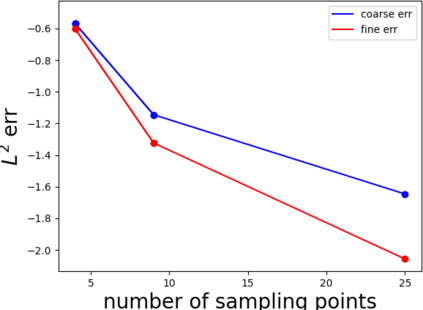
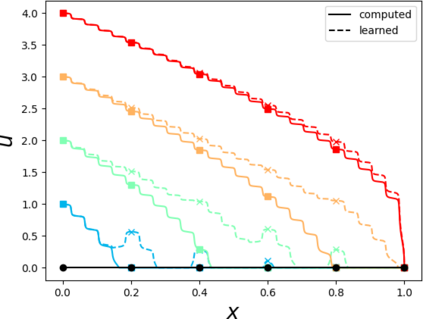
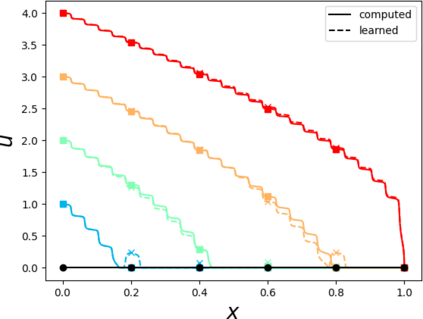
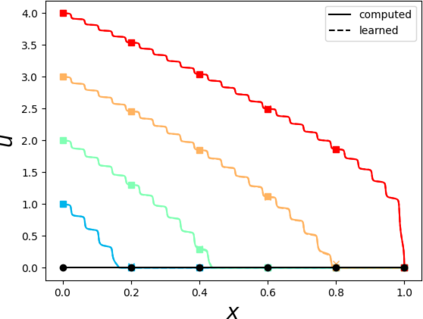
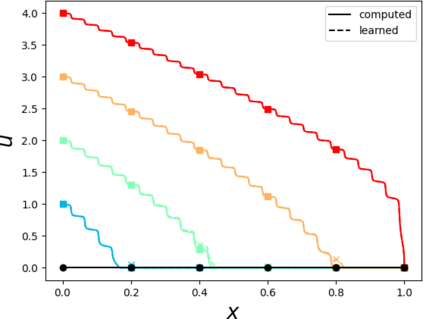
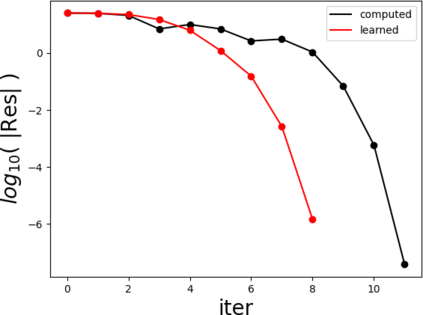
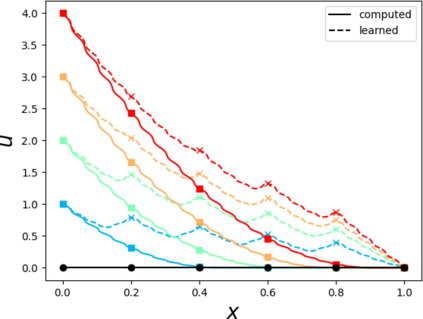
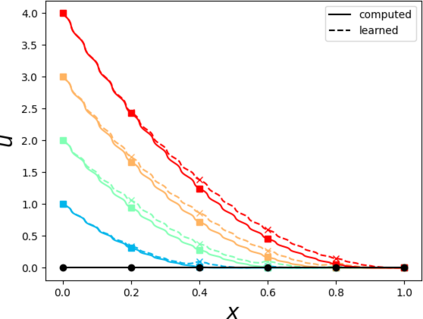
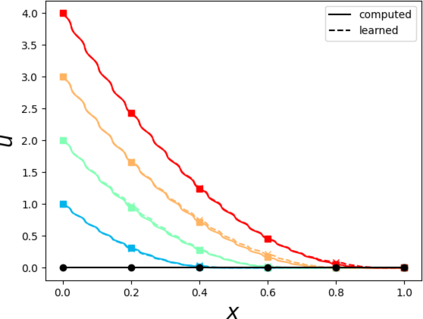
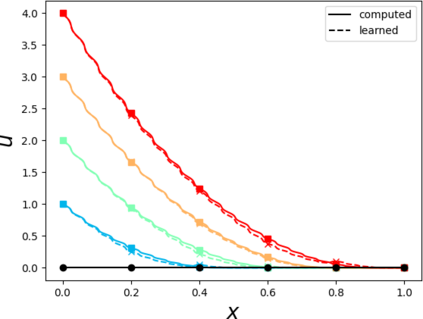
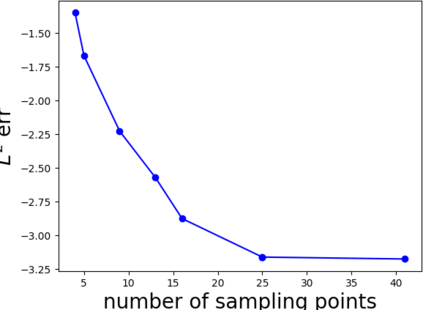
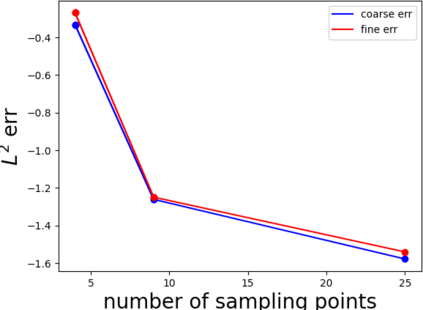
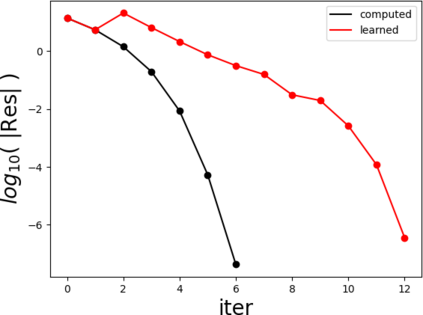
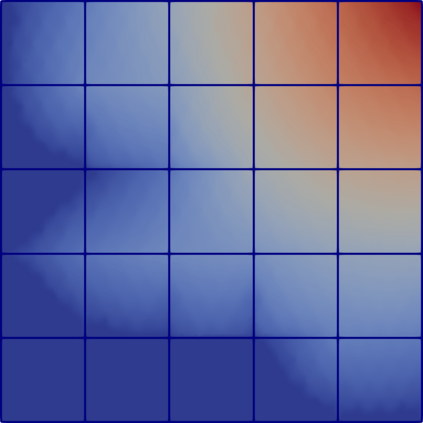
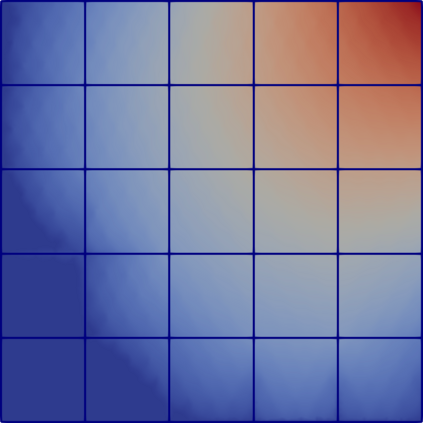
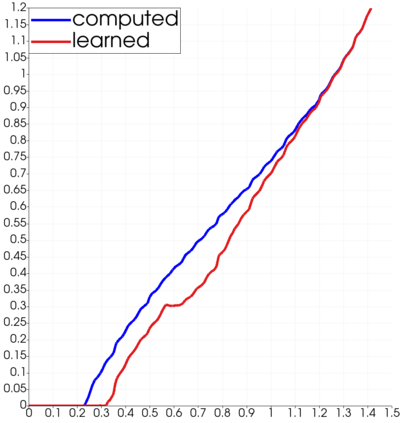
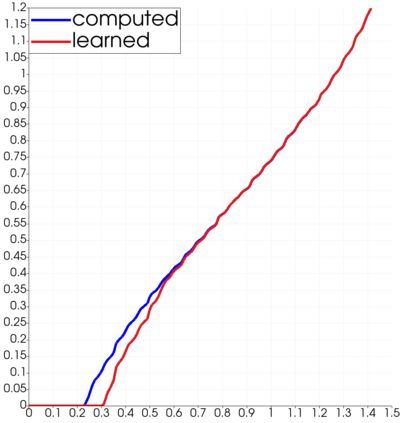
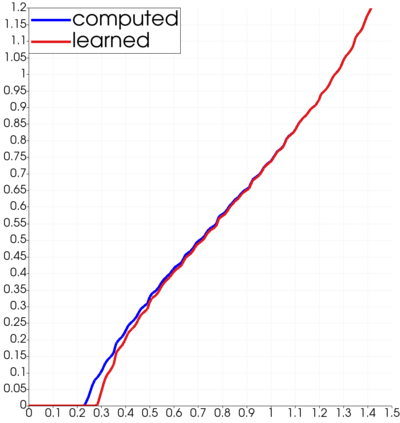
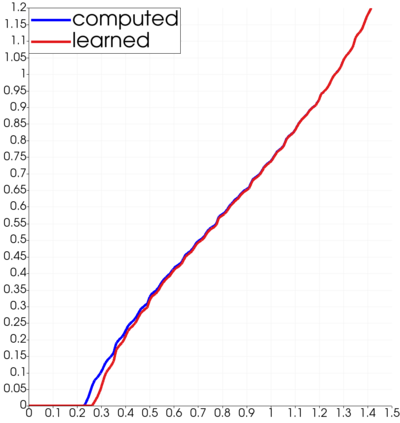
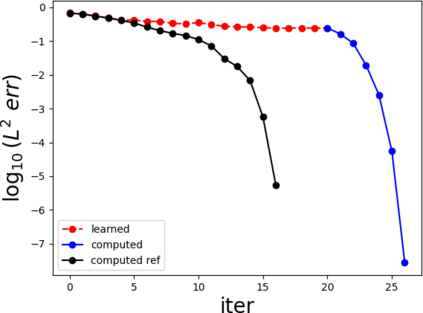
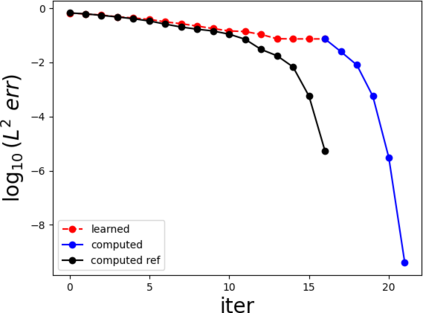
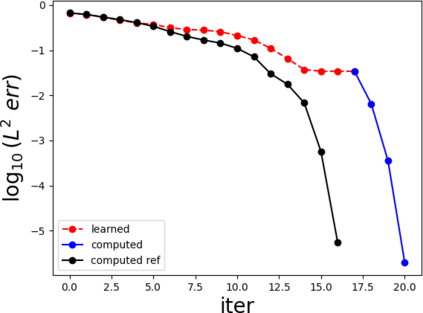
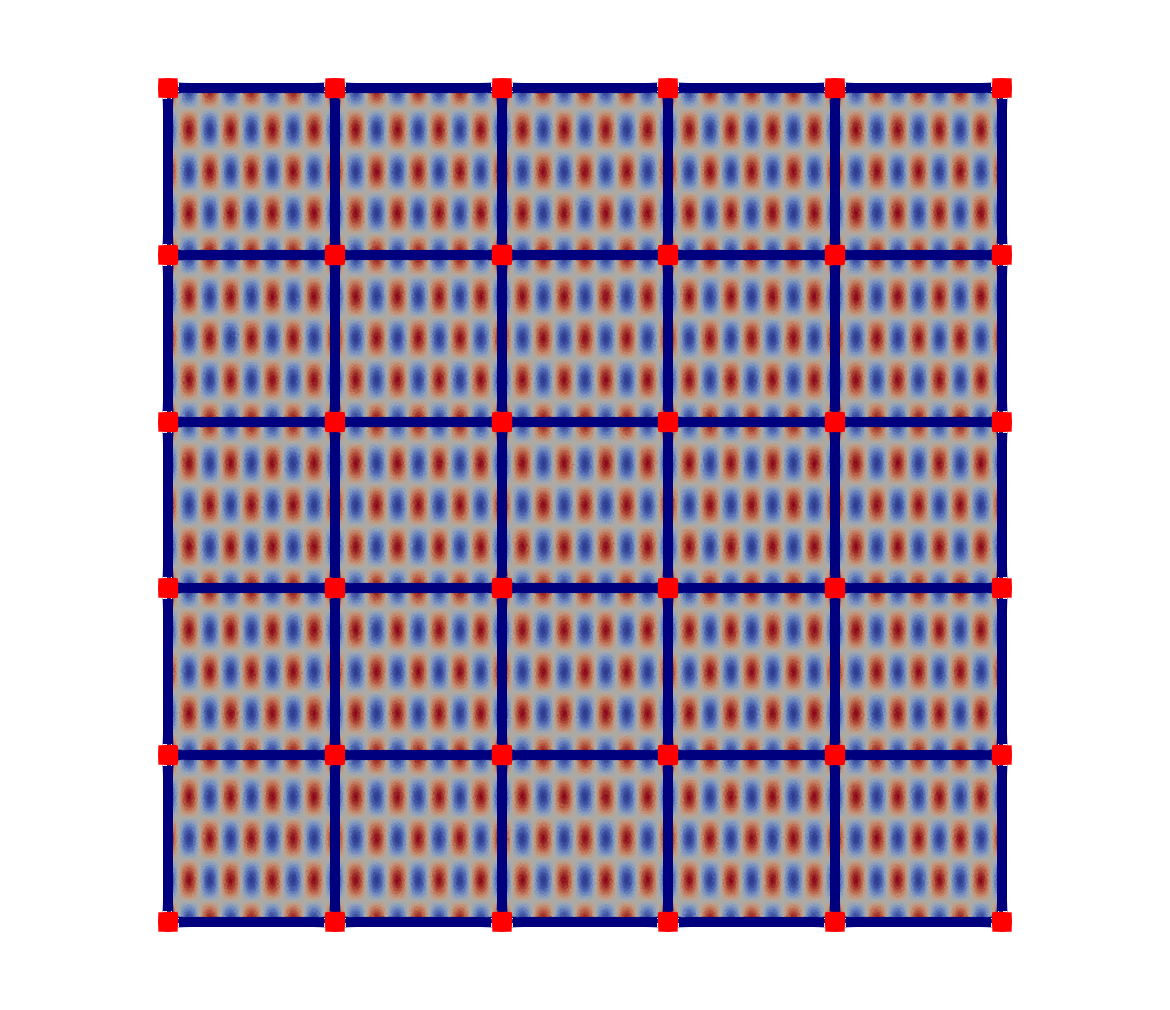
Partial differential equations (PDEs) involving high contrast and oscillating coefficients are common in scientific and industrial applications. Numerical approximation of these PDEs is a challenging task that can be addressed, for example, by multi-scale finite element analysis. For linear problems, multi-scale finite element method (MsFEM) is well established and some viable extensions to non-linear PDEs are known. However, some features of the method seem to be intrinsically based on linearity-based. In particular, traditional MsFEM rely on the reuse of computations. For example, the stiffness matrix can be calculated just once, while being used for several right-hand sides, or as part of a multi-level iterative algorithm. Roughly speaking, the offline phase of the method amounts to pre-assembling the local linear Dirichlet-to-Neumann (DtN) operators. We present some preliminary results concerning the combination of MsFEM with machine learning tools. The extension of MsFEM to nonlinear problems is achieved by means of learning local nonlinear DtN maps. The resulting learning-based multi-scale method is tested on a set of model nonlinear PDEs involving the $p-$Laplacian and degenerate nonlinear diffusion.
翻译:暂无翻译
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem