Hierarchical Optimal Transport for Unsupervised Domain Adaptation

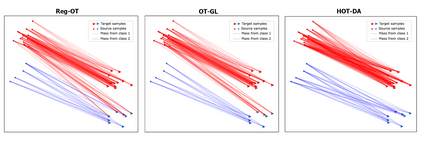
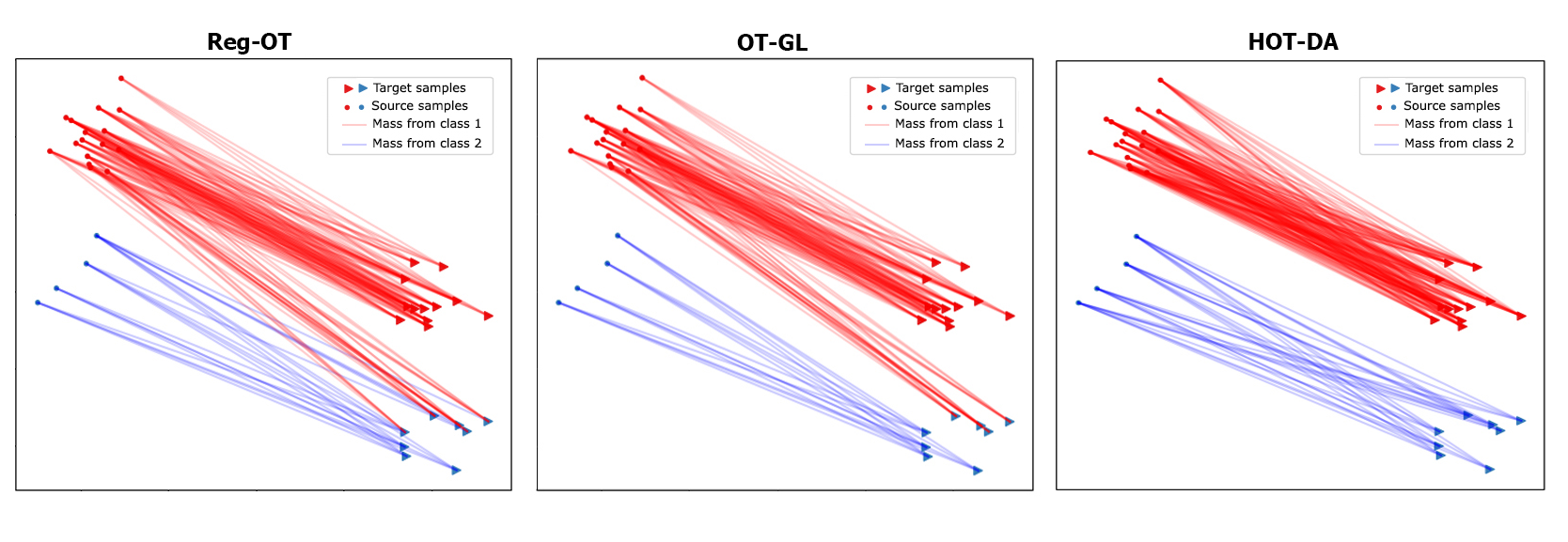
In this paper, we propose a novel approach for unsupervised domain adaptation, that relates notions of optimal transport, learning probability measures and unsupervised learning. The proposed approach, HOT-DA, is based on a hierarchical formulation of optimal transport, that leverages beyond the geometrical information captured by the ground metric, richer structural information in the source and target domains. The additional information in the labeled source domain is formed instinctively by grouping samples into structures according to their class labels. While exploring hidden structures in the unlabeled target domain is reduced to the problem of learning probability measures through Wasserstein barycenter, which we prove to be equivalent to spectral clustering. Experiments on a toy dataset with controllable complexity and two challenging visual adaptation datasets show the superiority of the proposed approach over the state-of-the-art.