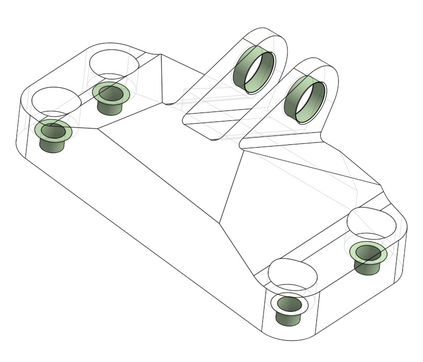
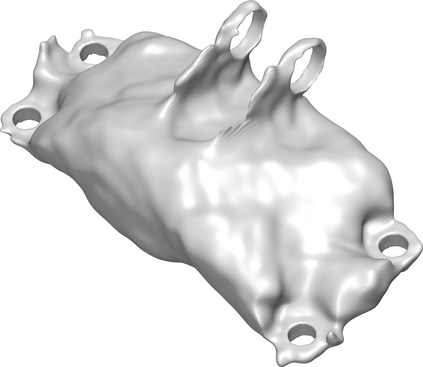
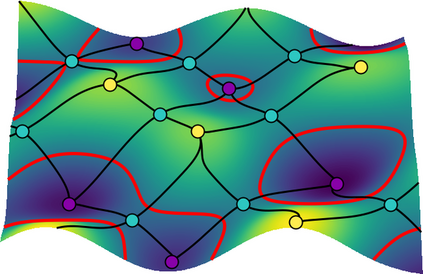
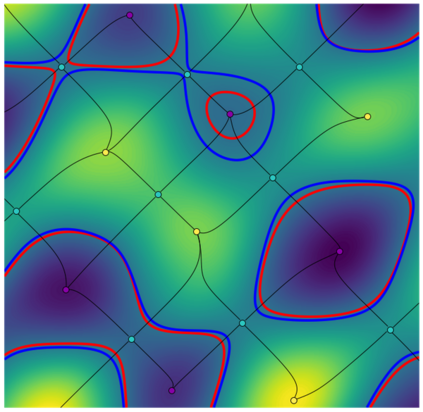
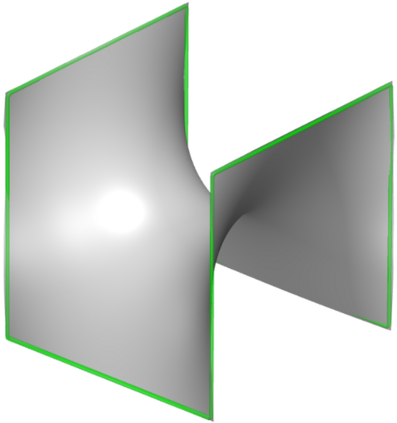
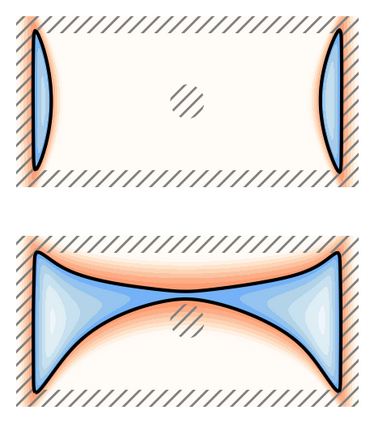
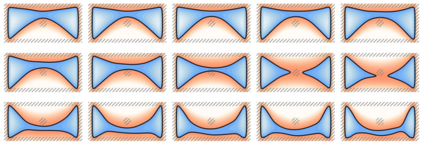
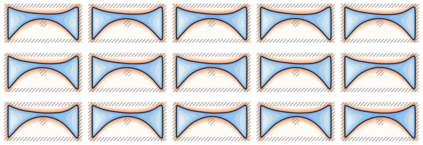
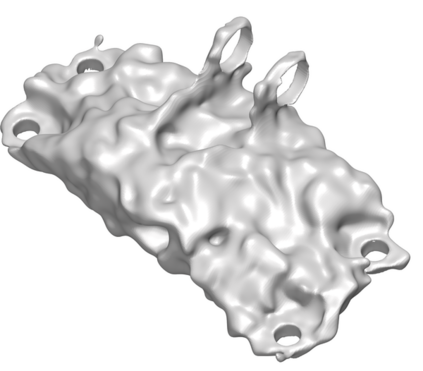
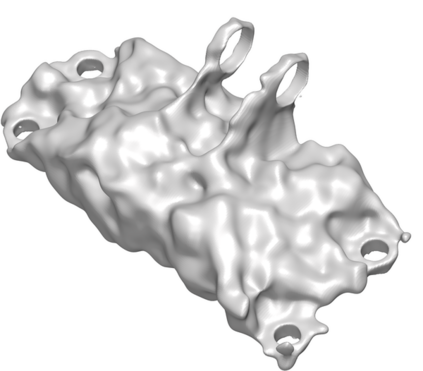
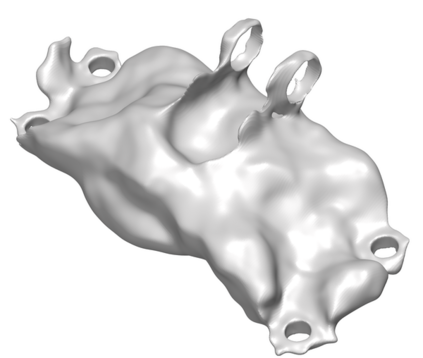
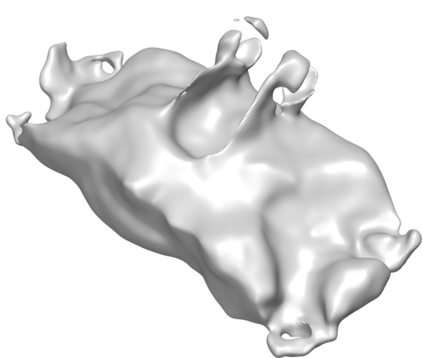
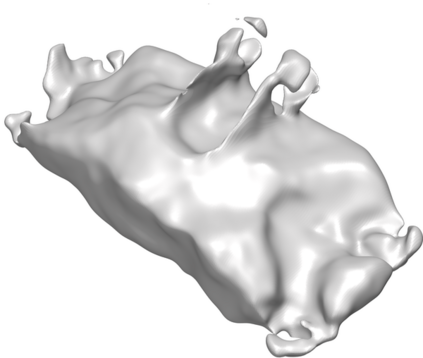
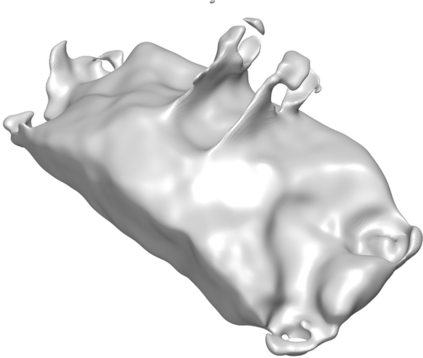
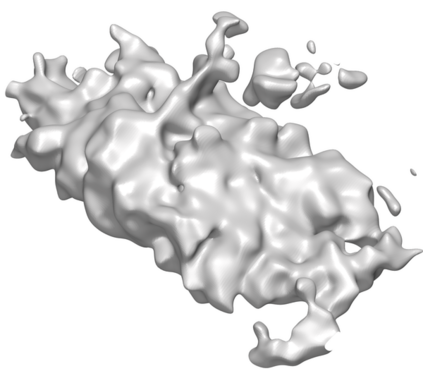
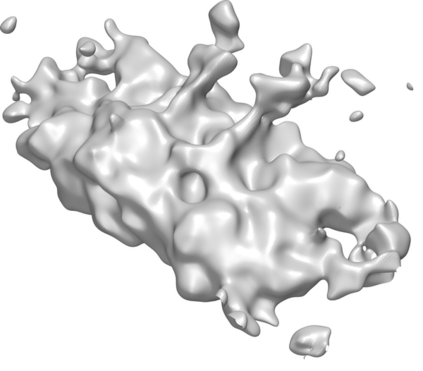
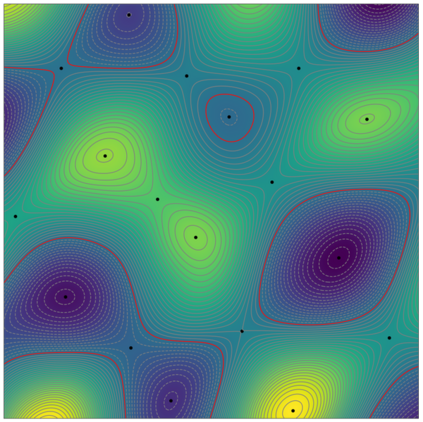
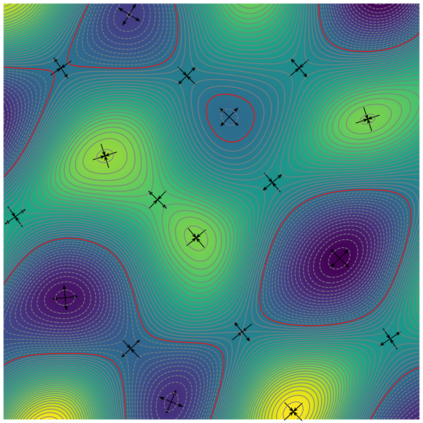
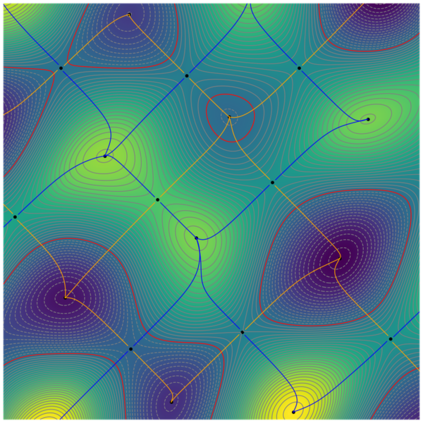
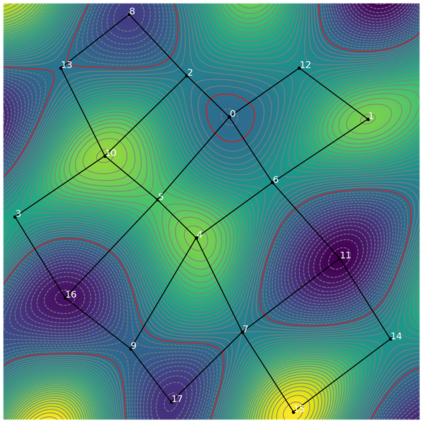
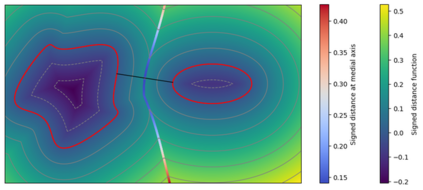
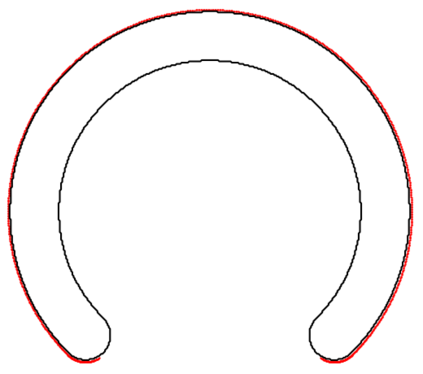
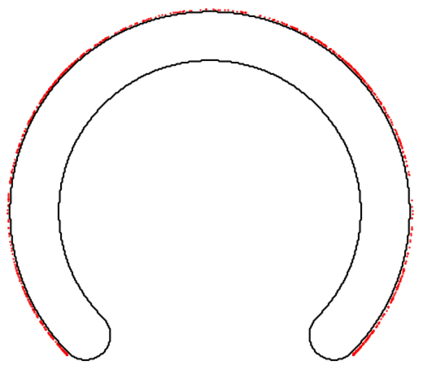
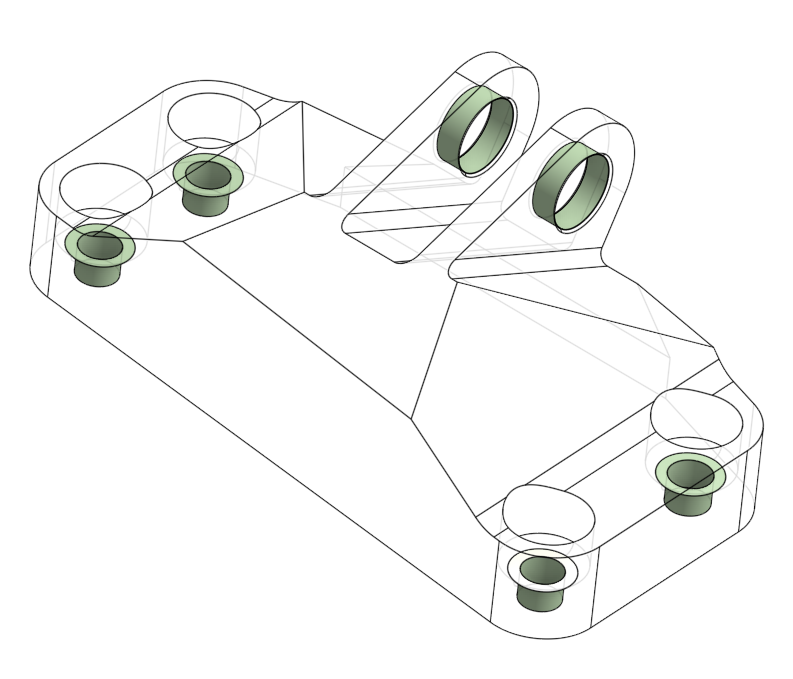
We introduce the concept of geometry-informed neural networks (GINNs), which encompass (i) learning under geometric constraints, (ii) neural fields as a suitable representation, and (iii) generating diverse solutions to under-determined systems often encountered in geometric tasks. Notably, the GINN formulation does not require training data, and as such can be considered generative modeling driven purely by constraints. We add an explicit diversity loss to mitigate mode collapse. We consider several constraints, in particular, the connectedness of components which we convert to a differentiable loss through Morse theory. Experimentally, we demonstrate the efficacy of the GINN learning paradigm across a range of two and three-dimensional scenarios with increasing levels of complexity.
翻译:暂无翻译