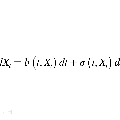若干类ABSDEs以及其他类型BSDEs的研究

项目名称： 若干类ABSDEs以及其他类型BSDEs的研究

项目编号： No.11626236

项目类型： 专项基金项目

立项/批准年度： 2016

项目学科： 数理科学和化学

项目作者： 吴浩

作者单位： 中南民族大学

项目金额： 2.5万元

中文摘要： 该项目主要研究以下几个方面内容：首先，研究 GABSDEs, 选取适当连续增过程，我们研究由该类增过程和标准 Brown 运动驱动的GABSDEs解的存在唯一性和解的比较定理，同时将其运用随机控制论中；此外，假设生成子满足线性增长条件，得到GABSDEs最小解的存在性。其次，我们研究由 Markov chain 驱动的 ABSDEs 在线性增长条件下的最小解的存在情况，在文献[27]得到由Markov chain 驱动的ABSDEs解得比较定理的基础上，我们仿照文献[7，34]中的方法得到该类方程最小解的存在性；最后，在一般流的条件下，我们研究 ABSDEs 解得存在唯一性，比较定理以及方程最小解的存在性并将这类方程运用到最优控制问题中去。

中文关键词： 随机微分方程；倒向随机微分方程；随机最优控制；概率论；随机过程

英文摘要： The research mainly includes the following aspects: firstly, we study GABSDEs which are diven by a proper continous increasing process and a Brownian motion. Choosing the appropriate continuous increasing processes, under some certain assumptions, we stud

英文关键词： stochastic differential eqiations；Backward stochastic differential eqiations；Stochastic optimal control；Probability；Stochastic processes