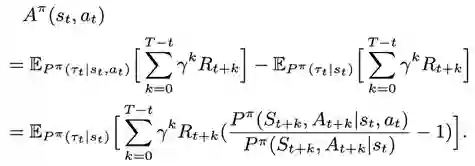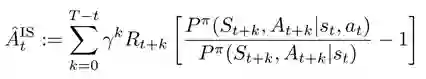IJCAI 2021 | 一文了解微软亚洲研究院机器学习方向前沿进展

(本文阅读时间:15 分钟)
论文链接:
https://www.ijcai.org/proceedings/2021/0461.pdf
在强化学习中,优势函数 (advantage function) 普遍采用蒙特卡洛 (MC)、时间差分 (TD),以及一种将前两者结合的优势函数估计算法(GAE) 等进行估计,而这些算法都存在方差较高的问题。因此,微软亚洲研究院的研究员们首次提出通过利用环境中存在于当前动作和未来状态之间的独立性,来降低优势函数估计中的方差。
在该方法中,存在于环境中的独立性可以用来构建一个基于重要性采样 (importance sampling) 的优势函数估计量。该估计量可以忽略未来无关的部分奖励,从而减小估计中的方差。为了进一步减少优势函数估计的方差,研究员们把该估计量和已有的蒙特卡洛估计量进行融合,并将最终的优势函数估计量命名为 IAE (Independence-aware Advantage Estimation)。实验结果表明,在策略优化算法中,IAE 与现有的优势函数估计方法 (GAE, MC) 相比,达到了更高的样本利用率。
事实上,现有方法往往先估计值函数 Q(s,a) 和 V(s),再将二者相减,进而估计优势函数。但当值函数覆盖的时间范围较大时,估计值函数就需要考虑未来较长时间内的总奖励,因此导致了高方差的问题。
当环境中存在独立性时,优势函数的估计就不需要考虑环境中的部分奖励,从而使得估计中的方差减小。举个例子:假设智能体当前的任务是打乒乓球,在该环境下,智能体每赢得一分或输掉一分后,游戏的状态都会被重新设置到起始状态,并继续进行下一轮游戏。当对智能体每一个动作的优势函数进行估计时,由于智能体每个动作的影响都被限制在当前回合内,所以下一轮及之后的奖励实质上不影响优势函数的估计。
上述例子表明,如果执行当前的动作不影响未来某些状态的概率,那么这些未来状态上的奖励在估计优势函数时就可以被忽略。研究员们对上述观察进行了概括和抽象,并提出了基于重要性采样的优势函数估计量。下面给出的是基于重要性采样推导出来的该估计量的形式:
此公式证明了如下的估计量是优势函数的无偏估计量:
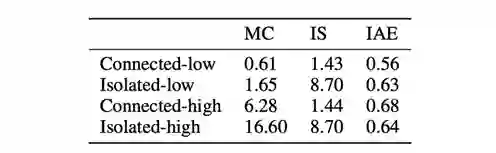
表1:不同设置下 IAE、MC、IS 的标准差
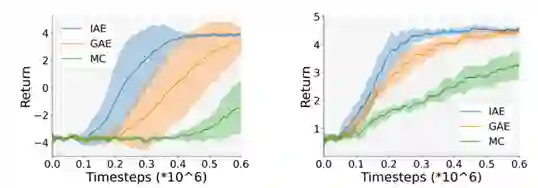
图1:PPO 算法在不同优势函数估计方法下的训练曲线
面向合作与非合作任务的多智能体强化学习方法MFVFD
论文链接:
https://www.ijcai.org/proceedings/2021/0070.pdf
多智能体强化学习(Multi-agent Reinforcement Learning, MARL) 有望帮助解决各种现实世界中的问题。然而,追求有效的MARL 面临着两大挑战:部分可观察性和可扩展性限制。为了应对这两大挑战,并使得 MARL 适用于竞争任务、合作任务以及混合任务,微软亚洲研究院和北京大学的研究员们在中心训练分散执行(Centralized Training with Decentralized Execution,CTDE)的框架下,从个体值函数分解 (Value Function Decomposition,VFD)的角度,结合平均场理论(Mean Field Theory,共同提出了一种新颖的多智能体 Q 学习方法——MFVFD。
正所谓“非宅是卜,唯邻是卜”,如果邻里和睦,则利人利己;而邻里不和,则多是非。也就是说,在多智能体系统中,个体不仅要考量最大化自身的利益,也要考量其临近智能体的行为对齐本身的影响。比如,在足球环境中,球员射门得分与否,除去依赖球员个体自身的射门能力之外,还会受到近邻智能体的影响,即优秀的队友与糟糕的对手会促进得分,而糟糕的队友和优秀的对手则会阻碍得分。
为了研究多智能体如何在既有合作又有竞争的环境下的表现,研究员们基于平均场理论将个体在多智能体系统中基于全局信息的动作值函数,近似为基于局部信息估计的个体动作值函数与基于近邻信息的平均场影响函数的和,公式如下:
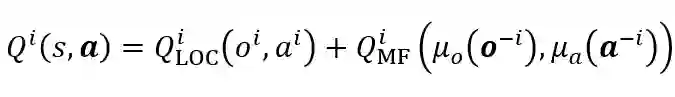
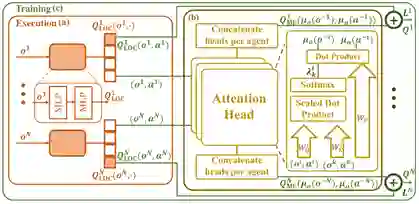
其中,Q_LOC^i 为基于局部信息的个体 i 的动作值函数,用于动作选择;Q_MF^i 为基于近邻信息的平均场影响函数,用于辅助对 Q_LOC^i 的估计。考虑到智能体不同近邻的重要性不同,所以研究员们使用注意力机制(Attention)建立了单体与近邻的权重 λ^i (o^i,o^k,a^i,a^k),并基于此计算带有重要性权重的近邻观测分布 μ_o (o^(-i) ) 和动作分布 μ_a (a^(-i) ) ,以构建平均场影响函数 Q_MF^i。
图2:MFVFD 网络结构图
在主试验部分,研究员们选取了 MAgent Battle 任务,对 MFVFD 在具有大规模智能体且具有部分观测的限制下的性能进行了验证。在该任务中,红蓝双方各具有400个智能体,每个智能体具有局部观测,且无法通讯,其通过消灭敌人来获得奖励。由于每个智能体以优化各自的奖励为目标,所以单体会与同伴竞争杀敌数量,来获取更多的个人奖励。除此之外,单体还会与同伴配合避免被杀害,以消灭所有敌人获取更多的团队奖励。因此,这是一个合作和竞争混合的复杂任务。如图3所示,MFVFD(红色)与基线方法的(蓝色)相比,学会了更难的团体配合的围歼策略,取得了胜利。从对抗胜率上可以看出,MFVFD 在所有的基线方法中,几乎处于不败地位。
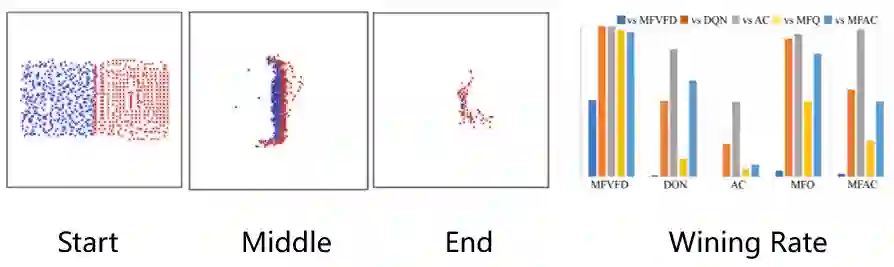
图3:MFVFD 与基线方法相比
此外,研究员们还选取了三个任务对 MFVFD 方法进行了理论分析,分别是:重复矩阵博弈任务----鹰鸽博弈与非单调合作博弈;合作导航任务----Cooperative Navigation;交通任务----Traffic Benchmark。从长远来看,MFVFD 在实际环境中能够有实际可行的研究价值。
CUC:云计算中基于不确定约束的预测作业调度算法

论文链接:
https://www.ijcai.org/proceedings/2021/0499.pdf
在云计算中,由于需求的庞大和多样性,平台计算资源的容量管理一直是一个极大的挑战。为了更好地根据整个云计算平台的容量进行规划,平台往往会提前收集一部分非即时的计算作业需求,这些计算作业可以持续运行指定长度的时间,且起止时间更加灵活。通过根据非即时计算作业的需求和平台在未来一段时间内的容量情况来进行统一调度,有助于平衡整个平台的工作负荷,提升平台资源的利用效率。但是,由于平台上未来可用的计算容量是不确定的,所以对这些非即时作业的调度,在不确定的计算资源约束下进行安排是一个巨大的挑战。
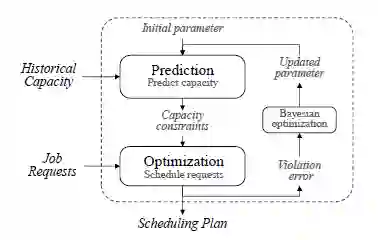
对于具有不确定约束的优化问题,传统的优化方法无法直接进行求解,而是需要结合对不确定约束进行预测的步骤来进行优化。然而,单独进行预测和优化的两阶段方法有明显的不足之处:两阶段方法假设预测结果是准确的,可是在实际中预测误差却无法避免,从而导致优化得出的解会违反(violate) 约束。
图4:CUC 方法的架构
此外,研究员们还针对实际应用中难以避免的违反约束情况,提出了相应的控制方式。该方式可以根据系统的要求,将实际违反约束的比例控制在特定水平以下,使得调度方案更加可靠与稳健。
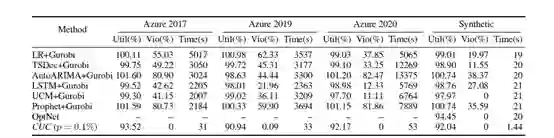
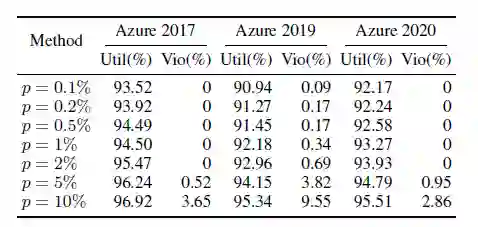
为了验证 CUC 算法的有效性,本文将 CUC 算法与包含经典预测方法以及精确优化求解方法的两阶段法进行了对比,结果如表2和表3所示。结果表明 CUC 算法可以高效准确地得到违反约束比例很小的调度方案,同时可以尽可能使得更多的作业得到调度。而且通过改变违反约束水平的参数p,CUC 算法也可以灵活控制实际的违反约束情况出现的比例,以满足不同系统对于调度方案的实际违反约束情况的要求。
表2:不同方法在公开数据集上的表现对比
表3:不同违反约束水平参数 p 下,CUC 方法的表现
用于学习三维隐式符号距离场的样条位置编码

论文链接:
https://www.ijcai.org/proceedings/2021/0151.pdf
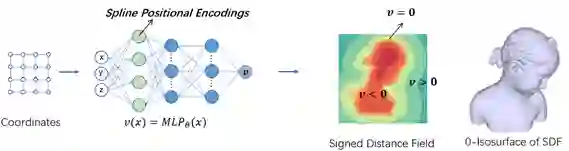
近日,全连接神经网络(MLP) 被提出作为三维形状的隐式表达。MLP 以 3D 坐标为输入,可以直接输出该 3D 坐标点到三维形状表面的距离,即带符号的距离场(SDF),如图5所示。距离为正的点在三维形状外部,距离为负的点在三维形状内部,距离为0的点则代表三维形状本身。相对于传统的离散三维形状表达而言,MLP 的表达非常紧致,只需要极少量的存储就能表达复杂的形状,因而引起了科研人员的广泛关注。
图5:算法流程图
Spline Positional Encodings 可以帮助 MLP 更好地拟合三维形状的细节
在使用 MLP 从点云中重建 SDF 的任务中,微软研究院的研究人员发现,如果直接将 3D 坐标作为 MLP 的输入,那么输出的形状会被过度平滑,丢失高频细节(见图6-(a))。为了解决这一问题,研究员们提出将三维坐标通过一系列正弦/余弦函数映射到高维空间,即 Fourier Positional Encodings(见图6-(b)),然后再作为 MLP 的输入;或者将 MLP 中常用的 ReLU 激活函数替换为正弦函数(见图6-(c))。这些方法虽然能够拟合三维形状的几何细节,但是输出的 SDF 非常杂乱,其低频量无法被很好地重建。因此,微软研究院的研究员们提出了基于样条的位置编码,即 Spline Positional Encodings。该方法不仅可以重建三维形状的高频细节,还能够输出高质量的 SDF(见图6-(d))。
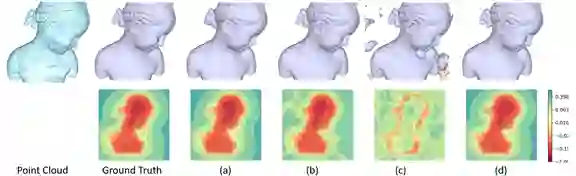
图6:各个方法的比较
Spline Positional Encodings 的结果如 (d) 所示
User-as-Graph: 基于异构图池化的新闻推荐用户建模

论文链接:
https://www.ijcai.org/proceedings/2021/0224.pdf
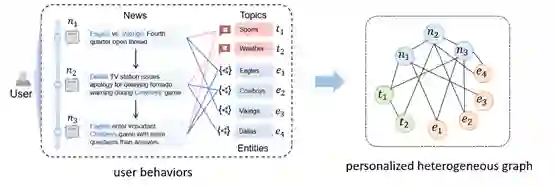
图7:个性化异构图的构建示例
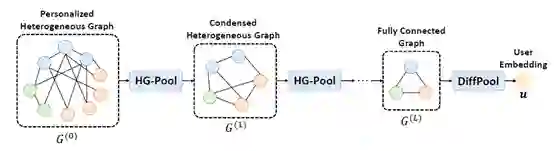
图8:从个性化异构图学习用户表示的迭代图池化过程
HG-Pool 方法的框架如图9所示。对于每种节点,首先使用一个不同的池化 GNN 模型来学习类型特定的节点表示。然后使用带 softmax 激活函数的线性变换,将这些节点表示转换为类型特定的池化矩阵。最后使用 padding 后的池化矩阵,将当前邻接矩阵和节点特征矩阵转换为更小的矩阵。
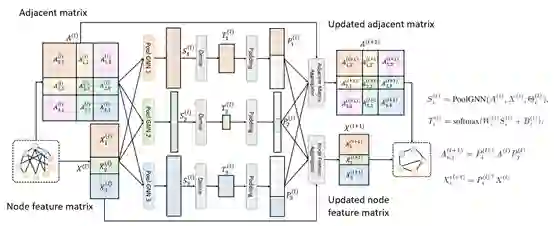
图9:HG-Pool的示意图
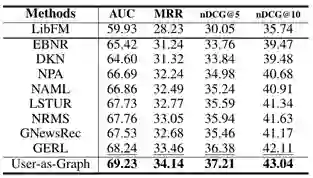
表4:不同方法在 MIND 数据集上的比较
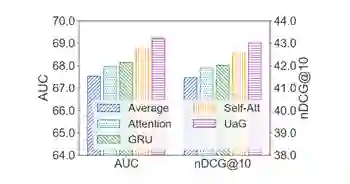
图10:不同用户建模方法的比较。UaG 是 User-as-Graph 的缩写
图11:不同图池化方法的比较
请在下面的选项中,选出你最感兴趣的论文题目,得票最高的论文,我们将邀请论文作者进行专题深度讲解!另外,此前推送的 IJCAI 2021 文章 “不确定性感知小样本图像分类模型,实现SOTA性能” 也参与到本次投票中,回顾详细内容可点击上述链接!
你也许还想看: