【深度学习基础】1.监督学习和最优化
如今深度学习如火如荼,各种工具和平台都已经非常完善。各大训练平台比如 TensorFlow 让我们可以更多的聚焦在网络定义部分,而不需要纠结求导和 Layer 的内部组成。本系列我们来回顾一下深度学习的各个基础环节,包括线性回归,BP 算法的推导,卷积核和 Pooling,循环神经网络,LSTM 的 Memory Block 组成等,全文五篇,前三篇是斯坦福深度学习 wiki 整理,第四第五两篇是 Alex Graves 的论文读书笔记,图片来自网络和论文,有版权问题请联系我们。

假如一个 target label 是与各种要素Xi呈线性关系的,我们可以用线性回归来拟合,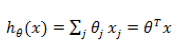
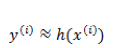
为了达到数据拟合的目的,可以用最小二乘的方法来训练调整参数 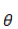
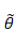
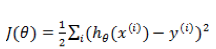
此问题的一类求解方法是通过梯度下降,每次对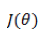
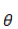
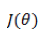
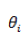
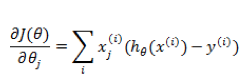
这个公式在编程的时候如何实现呢?首先我们把每一个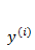
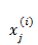
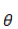
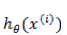
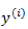
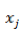
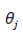
这样得到的偏导数也是一个向量,里面的元素与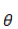
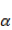
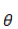
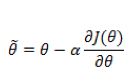
重复上述过程,直到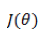
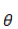
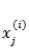
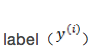
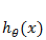
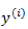
上面讲的线性回归可以用来预测连续值,但是很多时候我们希望做的是一个分类问题,也就是预测一个 instance 属于某个分类(比如:是/否,A/B/C等)的概率。逻辑回归就是完成此类任务的一个比较简单的方案。
在之前的线性回归的基础上,如果要预测的 y 是一个离散值(简单起见,后面以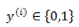
与上面的线性回归类似,现在我们的目标是找到一组参数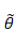
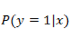
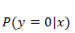
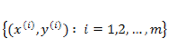
求 L 最大化的问题,同样可以通过求 -L 最小化来实现,与线性回归参数求解一样,同样通过梯度下降法来更新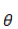
一旦我们求得了一组合适的参数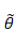
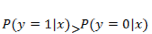
现在来看看通过梯度下降如何求借。通用需要对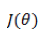
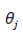
所以对前一部分求偏导 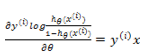
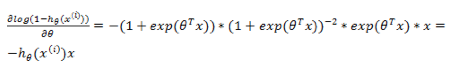
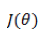
更新方式与线性回归类似:
程序实现上,同样先是拿到 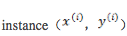
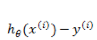
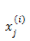
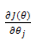
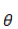
在程序开发的过程中,我们不可能对每个 instance 的每个位用 for 循环来操作,一般将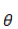
对于多条 instance 的 x 可以当做一个矩阵,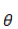
由于逻辑回归通常是对超高维的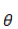
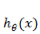
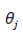
在进行开发的时候,有时候不确定我们的推导或者公式编码是否正确,这时候需要从数据上推断结果是否正确。有一个简单的办法是通过近似的导数来检查。
因此实际进行调试的时候,我们可以通过 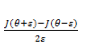
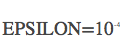
上面是对一维变量进行求导。如果是逻辑回归这样的参数,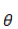
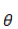
上面介绍的逻辑回归是一个二值化问题,y 的取值只有 0 和 1 ,如果我们的预测任务 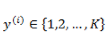
需要注意的是,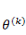
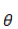
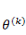
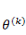
还是按照前面的套路,我们需要定义一个代价函数来定义模型对数据拟合的代价,并且通过最优化方法使得代价最小化。首先定义指示函数:
通过对所有 instance 拟合的概率最大化,有:
同样取负数把优化目标变为最小化,然后取 log ,得到代价函数:
下面的求导,为了推导方便,我们直接对 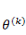
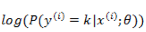
上式是对所有的 k 无差别化的求偏导,结合前面的系数 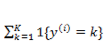
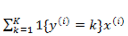
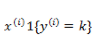
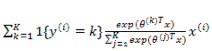
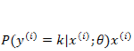
在编程实现的时候, 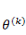
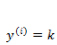
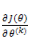
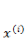
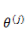
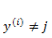
逻辑回归可以看做是 softmax regression 在 K=2 的时候的特殊情况,那么什么时候使用逻辑回归,什么时候使用 softmax regression 呢?举一个例子,对一篇讲金融和互联网结合的文章进行分类,如果你只允许每篇文章有一个分类值,选互联网就不能是金融,那么就用 softmax regression ,所有 K 个值是归一化的,每次只能输出一个概率最大值作为结果。如果允许给文章打上 <金融,互联网> 两个标签,则可以训练两个逻辑回归分类器,对金融和互联网的概率分别预测。
与逻辑回归的差别:上面我们提到 LR 和 softmax 都可以对 K=2 的任务进行回归预测,而且两种 label 的概率之和都是 1 ,看起来模型训练的时候,二分类问题用两种算法应该是没有区别的?其实不然,从上面的 softmax 求导过程可以发现 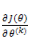
梯度下降法
此处可以延展开很多内容,比如随机梯度下降,牛顿法,L-BFGS 等。建议自己系统性的学习了解一下。


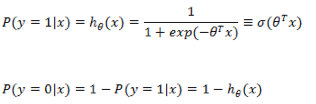
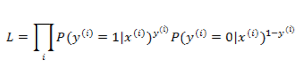
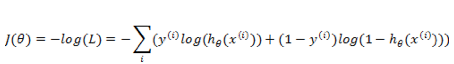
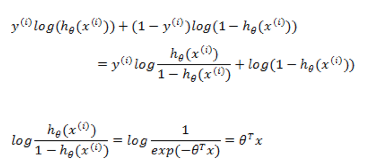
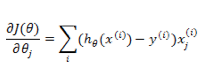
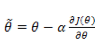
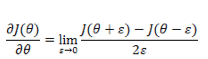
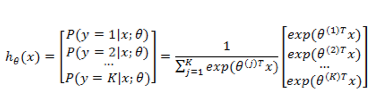
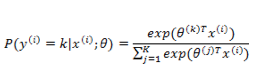
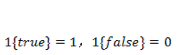
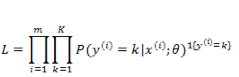
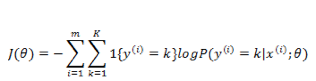
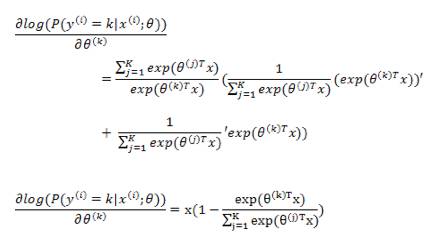
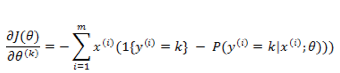

 微信ID:WeChatAI
微信ID:WeChatAI
 长按左侧二维码关注
长按左侧二维码关注