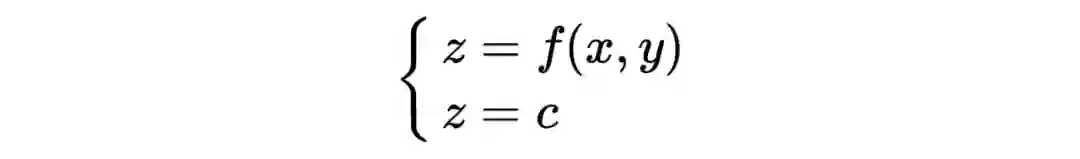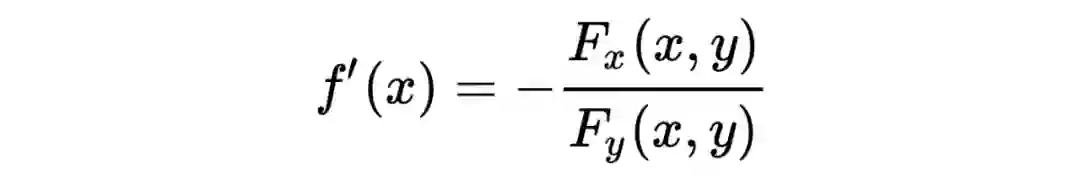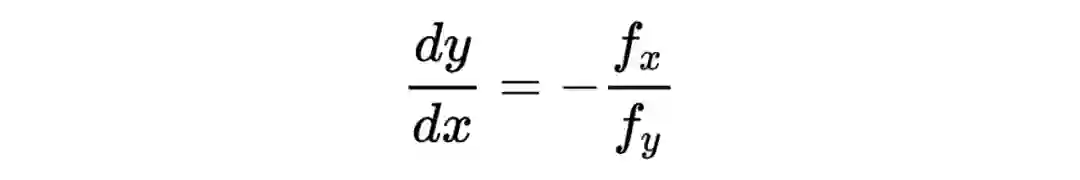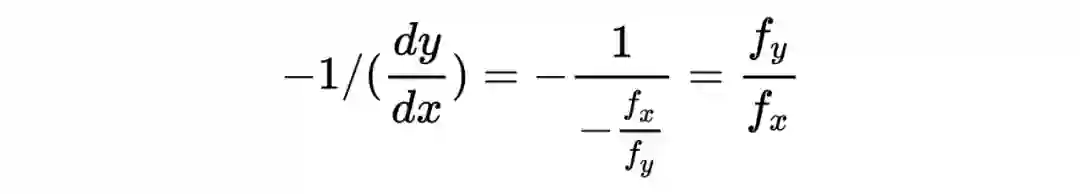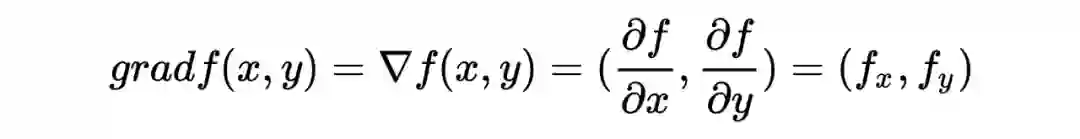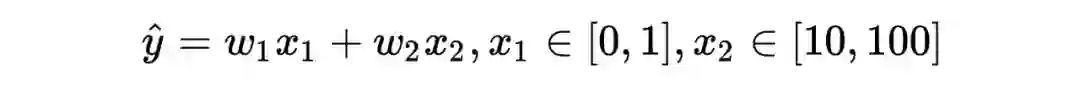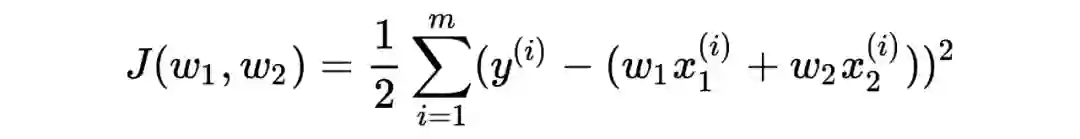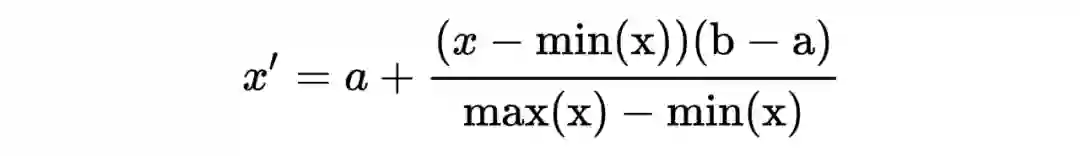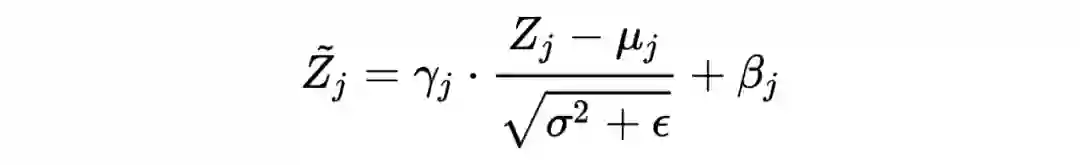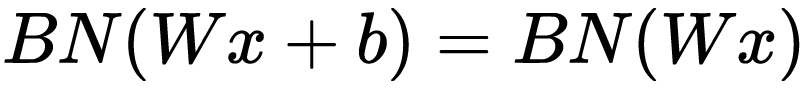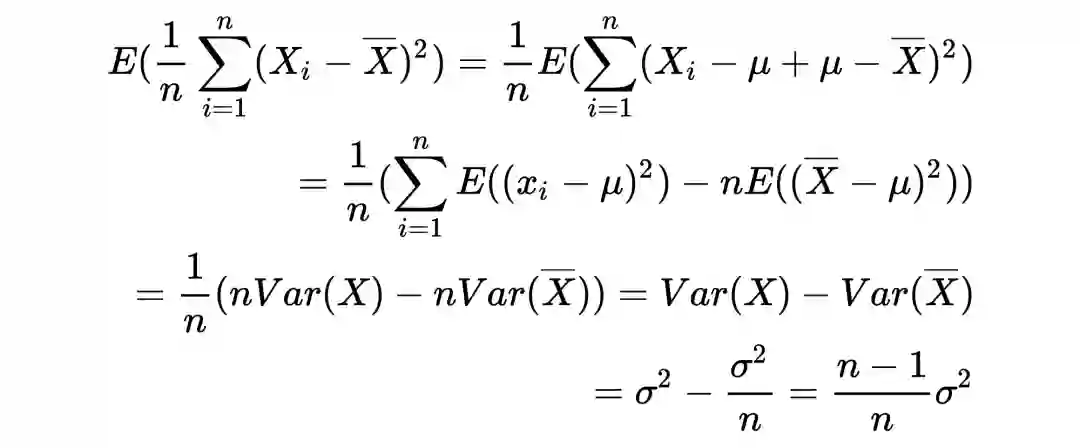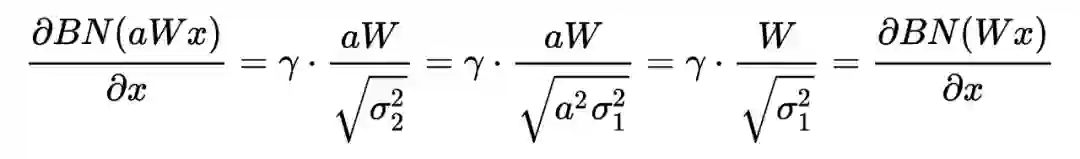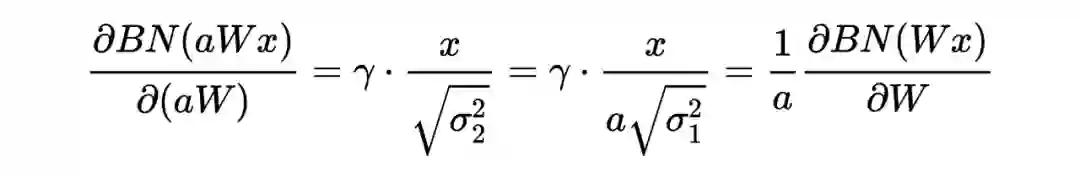归一化原来这么重要!深入浅出详解Transformer中的Normalization

什么是归一化?
-
为什要归一化?
从函数的等高线说起
1.1 函数的等高线是什么
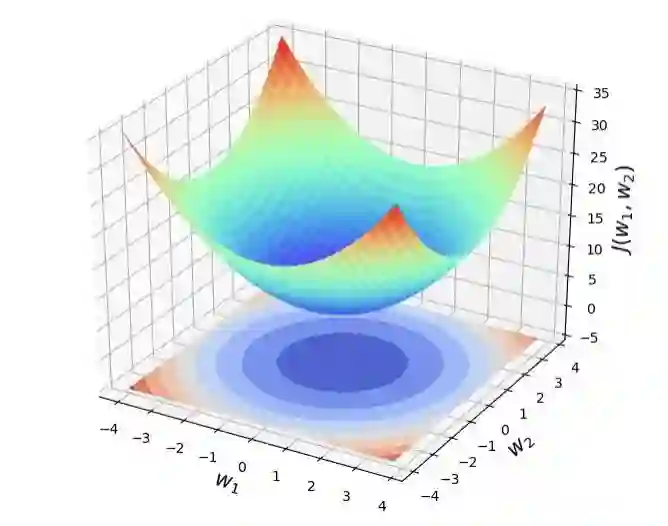
讨论一个二元损失函数的情况,即损失函数只有两个参数: 。
下图就是这个损失函数的图像,等高线就是函数 在参数平面 上的投影。
等高的理解:在投影面上的任意一个环中,所有点的函数值都一样。
等高的理解:在函数曲面上存在一个环,环上所有点的函数值一样,即距离投影平面的距离都一样。
-
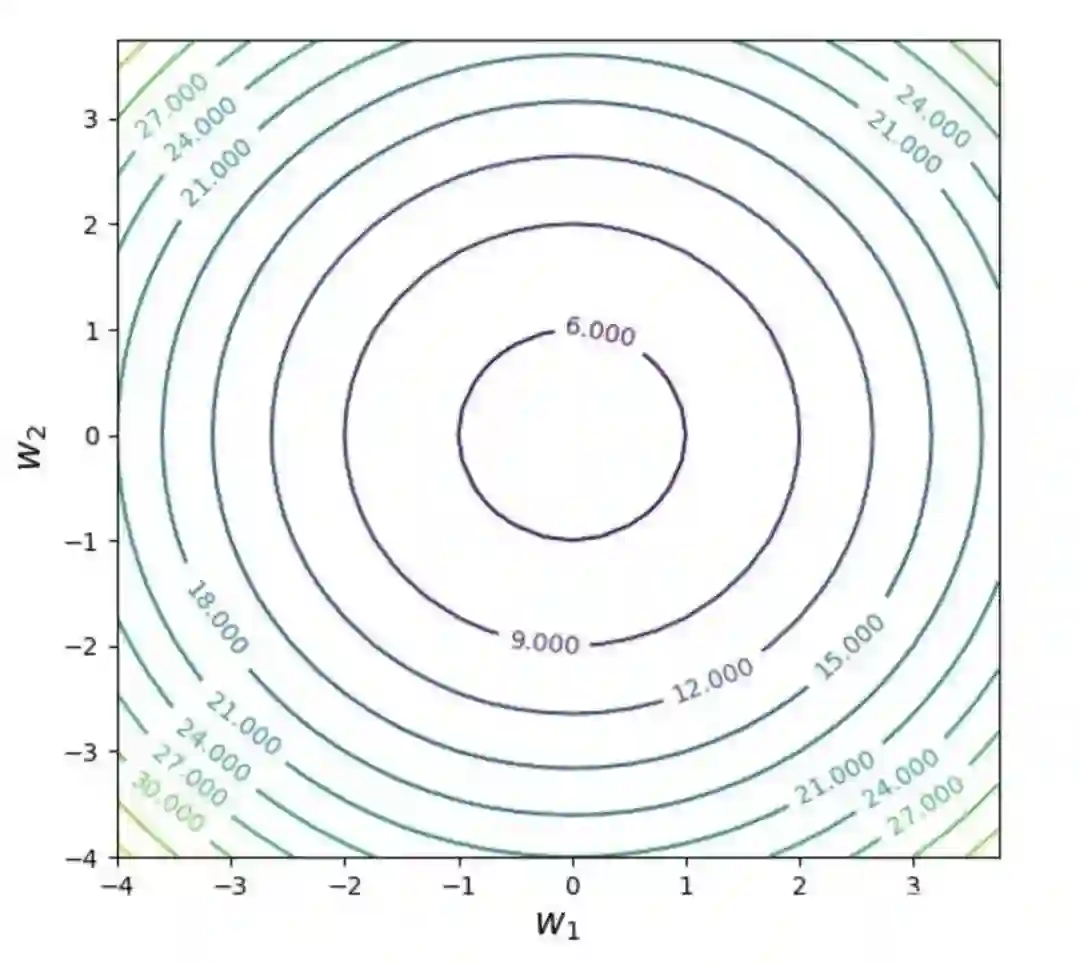
任意一个环上的不同参数取值 ,其函数值都一样。 -
可以看到,当 时,函数值 = 5,即全局最小点。
1.2 梯度与等高线的关系
假设存在一个损失函数 ,在空间中是一个曲面,当其被一个平面 ,c 为常数所截后,得到的曲线方程是:
曲线在 xoy 平面上的投影是一个平面曲线,即 ,即损失函数在 xoy 平面的某一条等高线,在这条等高线上,所有函数值均为 。
在这条等高线上,任意一点的切线斜率为 。
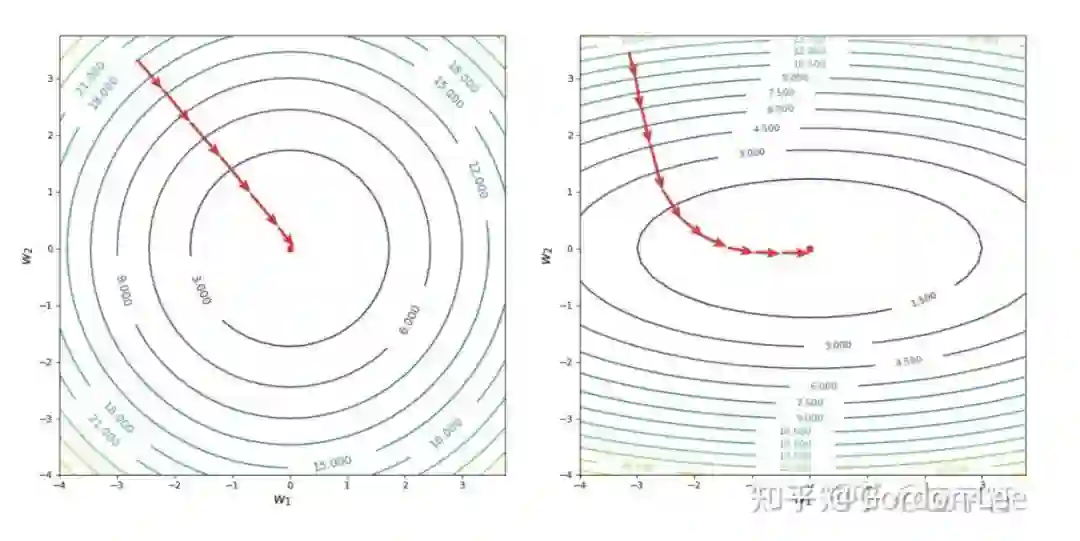
1.3 从等高线看为什么特征归一化
常见的特征归一化
上文我们讲了特征归一化,就是要让各个特征有相似的尺度。相似的尺度一般是讲要有相似的取值范围。因此我们可以通过一些方法把特征的取值范围约束到一个相同的区间。另一方面,这个尺度也可以理解为这些特征都是从一个相似的分布中采样得来。因此我们还可以通过一些方法使得不同特征的取值均符合相似的分布。
这里我们介绍一些常见的特征归一化方法的细节,原理和实现。
2.1 细节
rescaling (min-max normalization, range scaling)
standard normalization (z-score normalization)
scaling to unit length

2.2 原理
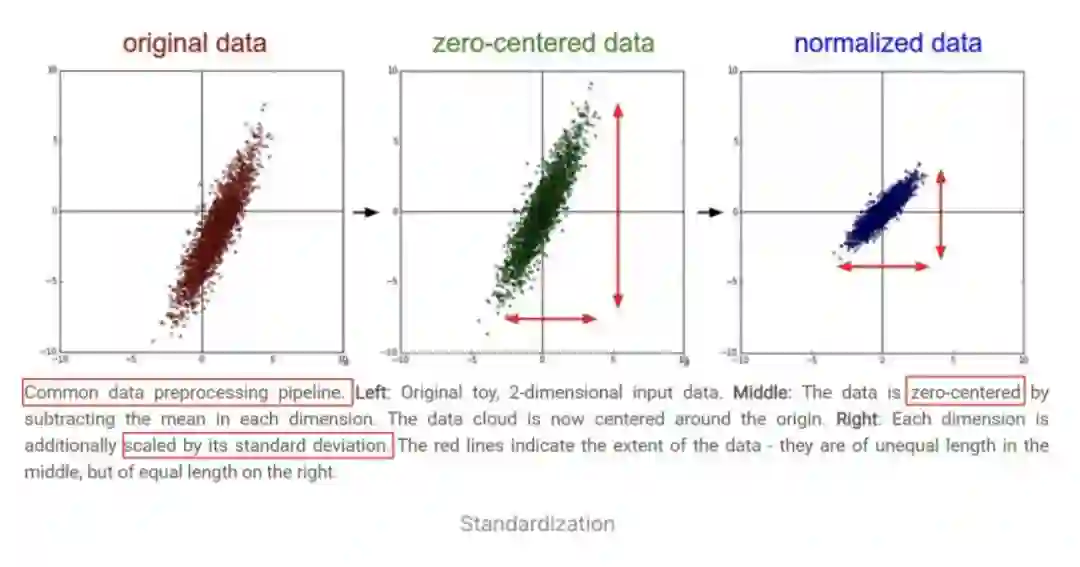
更直观地,可以从下图(来自于 CS231n 课程)观察上述方法的作用。下图是一堆二维数据点的可视化,可以看到,减去了每个维度的均值 以后,数据点的中心移动到了原点位置,进一步的,每个维度用标准差缩放以后,在每个维度上,数据点的取值范围均保持相同。
2.3 实现
上面我们讲了 4 种不同的归一化方式,但是需要注意一些细节。假设输入特征的形状是(B, d),即有 B 个样本,每个样本的特征是 d 维向量。
rescaling (min-max normalization, range scaling)
求最小值和最大值时,是对每一维,求所有样本的最大值和最小值。此时 axis=0,因为是沿着 0 轴操作的。
mean normalization
求均值时,是对每一维,求所有样本取值的均值,axis=0。
standard normalization
同上
scaling to unit length
-
计算的是向量的长度,每次计算的对象是某个样本上的所有维度,axis=1。
# rescaling (min-max normalization, range scaling)
>>> x
array([[ 1., -1., 2.],
[ 2., 0., 0.],
[ 0., 1., -1.]])
>>> np.min(x, axis=0)
array([ 0., -1., -1.])
>>> np.max(x, axis=0)
array([2., 1., 2.])
>>> (x - np.min(x, axis=0)) / (np.max(x, axis=0) - np.min(x, axis=0))
array([[0.5 , 0. , 1. ],
[1. , 0.5 , 0.33333333],
[0. , 1. , 0. ]])
# mean normalization
>>> x
array([[ 1., -1., 2.],
[ 2., 0., 0.],
[ 0., 1., -1.]])
>>> (x - np.mean(x, axis=0)) / (np.max(x, axis=0) - np.min(x, axis=0))
array([[ 0. , -0.5 , 0.55555556],
[ 0.5 , 0. , -0.11111111],
[-0.5 , 0.5 , -0.44444444]])
# standard normalization
>>> (x - np.mean(x, axis=0)) / np.std(x, axis=0)
array([[ 0. , -1.22474487, 1.33630621],
[ 1.22474487, 0. , -0.26726124],
[-1.22474487, 1.22474487, -1.06904497]])
>>> ((x - np.mean(x, axis=0)) / np.std(x, axis=0)).mean(0)
array([0., 0., 0.])
>>> ((x - np.mean(x, axis=0)) / np.std(x, axis=0)).std(0)
array([1., 1., 1.])
# scaling to unit length
>>> x
array([[ 1., -1., 2.],
[ 2., 0., 0.],
[ 0., 1., -1.]])
# 注意, 要记住设置keepdims=True, 否则广播的方向会错
>>> np.linalg.norm(x, ord=2, axis=1)
array([2.44948974, 2. , 1.41421356])
>>> np.linalg.norm(x, ord=2, axis=1, keepdims=True)
array([[2.44948974],
[2. ],
[1.41421356]])
>>> x / np.linalg.norm(x, ord=2, axis=1, keepdims=True)
array([[ 0.40824829, -0.40824829, 0.81649658],
[ 1. , 0. , 0. ],
[ 0. , 0.70710678, -0.70710678]])
>>> np.linalg.norm((x / np.linalg.norm(x, ord=2, axis=1, keepdims=True)), axis=1)
array([1., 1., 1.])
其他特征归一化方式:消除特征之间的相关性
继续以二维数据为例,总结下上面说的,先用 zero-mean 把数据移到原点,然后除以标准差去 normalize,让数据的分布更紧密:其实是让数据分布满足均值为 0(为什么均值为 0,因为所有的点减去了均值,整个数据的均值点平移到了0 点,所以为 0),方差为 1(为什么方差为 1,因为每一维特征都除以了每一维自己的标准差,这样每一维的标准差就为 1 了)。最后的结果就是数据分布满足看均值为 0,方差为 1 的特性。
然而这样还不够:从图中可以明显观察出,两个维度的特征存在相关性:x 轴的值增加,y 轴的值随之增加。我们希望一个好的表征应该是每个维度分别解耦的,独立表示一个事物,因此需要进一步消除各个维度之间的相关性,需要用到 PCA 和白化。
前置内容:Domain Adaption中的Covariate Shift
在讲传统机器学习的特征归一化在深度网络中的应用之前,先要讲下迁移学习中的领域自适应(DA)。在迁移学习中,源域有很多标注数据,目标域没有或者只有少量的标注数据,但是有大量无标注数据。比如常见的问题就是机器学习模型的泛化性问题,希望在 A 领域上训练的模型,能够在 B 领域也有比较好的性能。
源领域中的狗都是哈士奇,而目标领域中的狗都是拉布拉多,所以输入的边缘分布不同。
不管是什么狗,最后输出为狗的概率都为 1,也就是输出的label都要是狗,也就是条件分布相同,也就是学习任务是相同的。
-
解决这种情况的做法一般是学习一个 domain invariant 的 representation,也就是不管是什么领域的狗,最后输出都要是狗这个标签。

深度神经网络中归一化的作用
把传统机器学习中的特征归一化方法用在具有多个隐藏层的深度神经网络中,对隐藏层的输入进行归一化,也能够提升训练效率。其”可能“的原因有几派的观点:
5.1 更好的尺度不变性(即不同层输入的取值范围或者分布都比较一致)
一般上认为,深度神经网络中存在一种叫做 internal covariate shift(ICS)的现象:在深度神经网络中,一个神经层的输入是之前神经层的输出。给定一个神经层,它之前的所有神经层的参数变化会导致其输入的分布发生较大的改变。当使用随机梯度下降来训练网络时,每次参数更新都会导致该神经层的输入分布发生改变。越高的层,其输入分布会改变得越明显。就像一栋高楼,低楼层发生一个较小的偏移,可能会导致高楼层较大的偏移。
该现象会导致下面几个问题:
在训练的过程中,网络需要不断适应新的输入数据分布(其实就是之前讲的梯度更新迭代步数增多),所以会大大降低学习速度。
-
由于参数的分布不同,所以可能导致很多数据落入梯度饱和区,使得学习过早停止。 -
某些参数分布偏离太大,对其他层或者输出产生了巨大影响。
对比上面的概念就是:在神经网络的各层输出,由于它们经过了层内操作作用,其分布显然与各层对应的输入分布不同,而且差异会随着网络深度增大而增大。各层的输入和输出分布可以看作源领域和目标领域的输入边缘分布(因为这一层的输出分布也是下一层的输入分布),显然这两个分布已经变的不同了,但是其要预测的条件分布是相同的,因为两个输入预测出来的最后的 label 肯定要是一样的。
为了缓解 ICS 问题,需要对隐藏层的输入进行归一化,比如都归一化成标准正态分布,可以使得每个神经层对其输入具有更好的尺度不变性.不论低层的参数如何变化,高层的输入保持相对稳定。
5.2 更平滑的”优化地形“(optimization landscape)
在 NIPS 2018 的 How Does Batch Normalization Help Optimization?一文中,作者详细阐述了 batch normalization(一种用在 DNN 上的归一化方法)真正起作用的原因。该文中对 ICS 有了更精要的阐述,即该层的输入分布会因为之前层的更新而发生改变。同时,论文提出了两个问题,即 BN 的作用是否与 ICS 相关,以及 BN 是否会消除或减少 ICS。
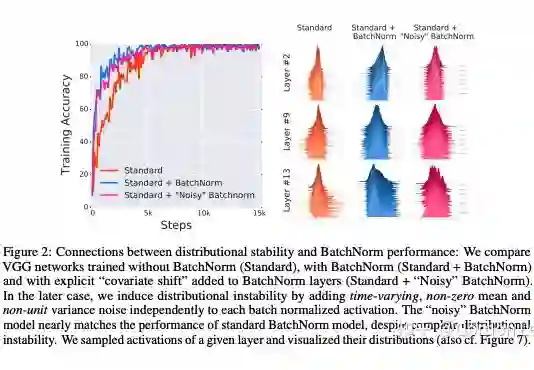
为了探究第一个问题,作者在 BN 层后面人为引入了一个随时间随机改变(该分布不容易被 DNN 学到)的噪声分布(即人为引入漂移现象,使得下一层的分布不再稳定)。结果发现,加了噪声以后,层的分布的稳定性(通过可视化每层采样一定神经元的激活值来度量分布的方差和均值)并不好,但是最后的效果依然很好,这说明 BN 层和 ICS 似乎没有啥关系。(因为加了 BN 层,虽然分布不稳定,但是效果依然好)。
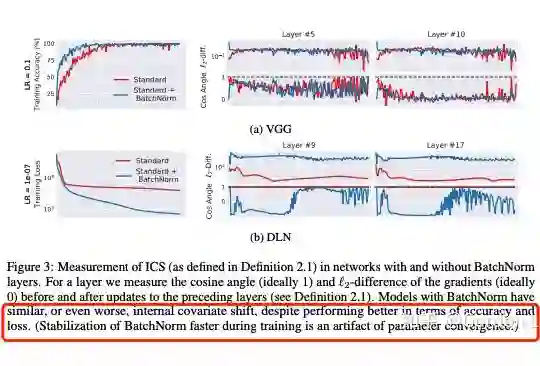
为了探究第二个问题,作者又设计了指标来量化 ICS 现象:通过测量更新到前一层和当前层的梯度差异(L2 距离)来量化一个层中的参数在多大程度上必须“调整”以应对前一层中的参数更新。理想来说,ICS 现象越小,上一层参数更新对当前层的分布影响越小,梯度变化程度越小。最后实验发现 BN 并不能减少 ICS,甚至可能还会有一定程度上的增加。
由此,作者认为 BN 层的作用可能和 ICS 没啥关系,也不能减少 ICS。
而作者认为,BN 的作用在于使得 optimization landscape 更加光滑。
神经网络的高维损失函数构成了一个损失曲面,也被称为优化地形(optimization landscape)。
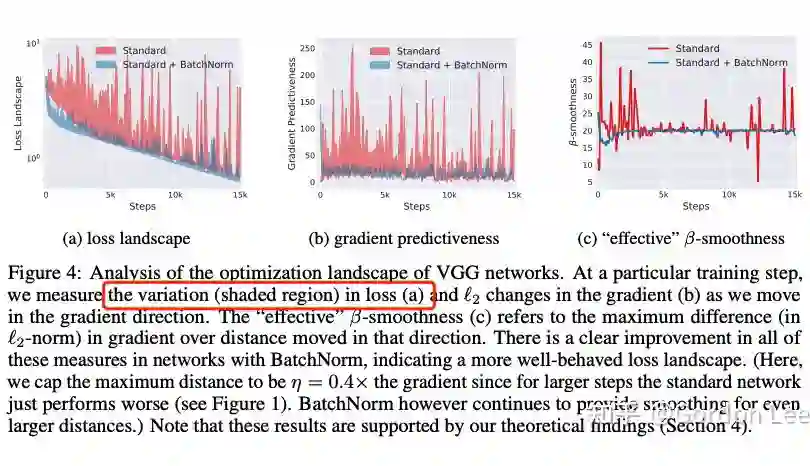
作者发现确实加了 BN 层以后,optimization landscape 更加光滑了。
进一步地,作者还以平滑优化地形为目标设计了另一种方法,结果发现和 BN 的效果差不多。这也说明了 BN 层的作用在于使得优化地形更加平滑。
5.3 总结
本节主要介绍了归一化方法(Batch Normalization)在深度神经网络中的作用:有人认为是更好的尺度不变性来缓解 ICS 现象。有人认为是更平滑的优化地形。当然,BN 层究竟怎么起作用的,现在还是没太探究清楚。实际上,咱们还没开始介绍 BN 是什么!!!哈哈哈,下一节就从缓解 ICS 现象的角度来讲解 BN 的原理和实现,并和之前讲过的机器学习中的归一化方法进行关联。
从缓解ICS现象出发
ICS 现象指的是该层的输入分布会因为之前层的参数更新而发生改变。为了缓解这一问题,我们需要对输入分布进行归一化。上上节讲了白化(其实还没填坑)是一种机器学习中常见的归一化手段,其好处在于:
能够使得逐层的输入分布具有相同的均值和方差(PCA 白化能够使得所有特征分布均值为 0,方差为 1)。
-
同时去除特征之间的相关性。
通过白化这一方法,可以有效缓解 ICS 现象,加速收敛。然而呢,其存在一些问题:
-
计算成本高(参见上上节还没填坑的计算过程,需要涉及到协方差,奇异值分解等)。 -
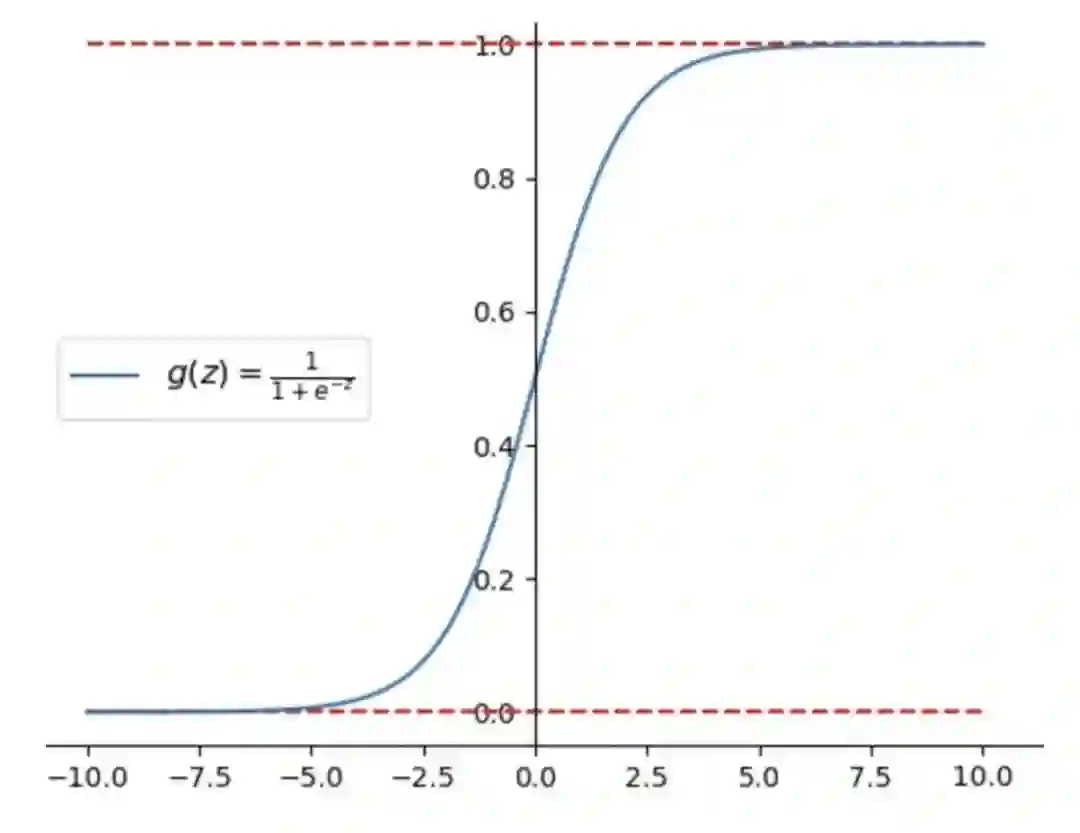
由于对输入分布进行了限制,会损害输入数据原本的表达能力(其实就是说原本数据的分布信息丢失了)。 均值为 0,方差为 1 的输入分布容易使得经过 sigmoid 或者 tanh 的激活函数时,落入梯度饱和区。
解决思路很简单:设计一种简化计算的白化操作,归一化后让数据尽量保留原始的表达能力。
单独对每一维特征进行归一化,使其满足均值为 0,方差为 1。
-
增加线性变换操作,让数据能够尽量恢复本身表达能力
Batch Normalization的算法过程
首先是对每一维特征进行归一化,可以借助上上节介绍的归一化方法:本质上是减去一个统计量,再除以一个统计量。另一方面,BN 的操作是在 mini-batch 层面进行计算,而不是 full batch。具体来说:
-
计算第 个样本的第 个维度上的均值: 。 -
计算第 个样本的第 个维度上的方差: 。 -
归一化: (加 防止分母为 0)。
通过上述变换实现每个特征维度上的均值和方差为 0 和 1。
通过上述变换,在一定程度上保证了输入数据的表达能力。
综上所述:
补充:在进行归一化过程中,由于归一化操作会减去均值,所以偏置项可以忽略或者置 0,即:
Batch Normalization在测试阶段的讨论
首先,在训练阶段,我们是对一个 mini-batch 的数据计算每个维度上的均值和方差。为什么不用全量数据的均值和方差呢?这样一来,不管哪个 batch 都用的一种分布了,会降低模型的鲁棒性。
在测试阶段,有可能只需要预测一个样本或者很少样本,不足以拼成一个 mini-batch,此时计算得到的均值和方差一定是有偏估计。为了解决这一问题,BN 的原论文中提出下面的方法:
注:为什么训练和测试的时候计算方差不一样呢?
训练时,计算当前 batch var 时,当前 batch 的样本就是该随机变量的所有样本了,因此除以 n 就好了。而测试时是全局样本的 var,因此当前 batch 的样本只是该随机变量的部分采样样本,为了是无偏估计,必须乘以 n/n-1。
在计算随机变量的均值和方差时,一般情况下无法知道该随机变量的分布公式,因此我们通常会采样一些样本,然后计算这些样本的均值和方差作为该随机变量的均值和方差。由于计算这些样本的方差时减的是样本均值而不是随机变量的均值,而样本均值是和采样的样本有关的,是有偏估计,如果要得到无偏估计,需要乘以 n/n-1。
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
x_stand = (x - running_mean) / np.sqrt(running_var)
out = x_stand * gamma + beta
再探讨:Batch Normalization的作用
-
更好的尺度不变性: 也就是说不管低层的参数如何变化,逐层的输入分布都保持相对稳定。尺度不变性能够提高梯度下降算法的效率,从而加快收敛。另一方面,归一化到均值为 0,方差为 1 的分布也能够使得经过 sigmoid,tanh 等激活函数以后,尽可能落在梯度非饱和区,缓解梯度消失的问题。 -
更平滑的优化地形: 更平滑的优化地形意味着局部最小值的点更少,能够使得梯度更加 reliable 和 predictive,从而让我们有更大的”信心”迈出更大的 step 来优化,即可以使用更大的学习率来加速收敛。 -
隐性的正则化效果: 训练时采用随机选取 mini-batch 来计算均值和方差,不同 mini-batch 的均值和方差不同,近似于引入了随机噪音,使得模型不会过拟合到某一特定的均值和方差参数下,提高网络泛化能力。 对参数初始化和学习率大小不太敏感:BN 操作可以抑制参数微小变化随网络加深的影响,使网络可以对参数初始化和尺度变化适应性更强,从而可以使用更大的学习率而不用担心参数更新 step 过大带来的训练不稳定。
卷积神经网络中的Batch Normalization实现
10.1 为什么CNN仅在channel维度上统计呢?
If the feature map was produced using convolutions, then we expect every feature channel's statistics e.g. mean, variance to be relatively consistent both between different images, and different locations within the same image -- after all, every feature channel is produced by the same convolutional filter! Therefore spatial batch normalization computes a mean and variance for each of the C feature channels by computing statistics over the mini batch dimension N as well the spatial dimensions H and W.
注:这部分的内容来源于尹相楠巨巨已经删除的内容
# coding=utf8
import torch
from torch import nn
# track_running_stats=False,求当前 batch 真实平均值和标准差,而不是更新全局平均值和标准差
# affine=False, 只做归一化,不乘以 gamma 加 beta(通过训练才能确定)
# num_features 为 feature map 的 channel 数目
# eps 设为 0,让官方代码和我们自己的代码结果尽量接近
bn = nn.BatchNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)
# 乘 10000 为了扩大数值,如果出现不一致,差别更明显
x = torch.rand(10, 3, 5, 5)*10000
official_bn = bn(x)
# 把 channel 维度单独提出来,而把其它需要求均值和标准差的维度融合到一起
x1 = x.permute(1,0,2,3).view(3, -1) # [N,C,H,W]==>[C,N,H,W]==>[C=3, N*H*W]
# 注意!!!!这里是把C维度单独弄出来,然后在剩下的维度上操作,所以dim=1
# 思维:统计的什么=沿着什么维度=操作的什么维度=dim就是那个
mu = x1.mean(dim=1).view(1,3,1,1) # [C, N*H*W]==>[C]==>[1, C, H, W]
std = x1.std(dim=1, unbiased=False).view(1,3,1,1)
# unbiased=False, 求方差时不做无偏估计(除以 N-1 而不是 N),和原始论文一致,个人感觉无偏估计仅仅是数学上好看,实际应用中差别不大
my_bn = (x-mu)/std
diff=(official_bn-my_bn).sum()
print('diff={}'.format(diff)) # 差别是 10-5 级的,证明和官方版本基本一致
10.2 在实现中需要注意的一点是:到底是对哪个维度求均值和方差
对于 shape 为 b x d 的张量来说,特征维度是最后一维:d。求均值和方差实际就是:对于 d 中的每一维,统计 b 个样本的均值和方差,均值和方差向量的形状为 (d)。实现:x.mean(dim=0)。
对于 shape 为 BCHW 的张量来说,如果是 batch Normalization,特征维度是 channel:C。求均值和方差实际就是:先 reshape:C, BHW,然后统计 BHW 个样本的均值和方差,均值和方差向量形状为 (C)。实现:x.permute(1,0,2,3).view(3,-1).mean(dim=1)。
总结来说:batch Normalization 实际是对特征的每一维统计所有样本的均值和方差,CNN 里面特征维度是 channel 维,所以最后向量形状就是 (C)。
提前说一下:Layer Normalization 实际是对每个样本的所有维度统计均值和方差,所以求和取平均的是 d 维度,最后向量形状就是 (B, max_len)

Batch Normalization的些许缺陷
要讲 Layer Normalization,先讲讲 Batch Normalization 存在的一些问题:即不适用于什么场景。
1. BN 在 mini-batch 较小的情况下不太适用。BN 是对整个 mini-batch 的样本统计均值和方差,当训练样本数很少时,样本的均值和方差不能反映全局的统计分布信息,从而导致效果下降。
2. BN 无法应用于 RNN。
RNN 实际是共享的 MLP,在时间维度上展开,每个 step 的输出是(bsz, hidden_dim)。由于不同句子的同一位置的分布大概率是不同的,所以应用 BN 来约束是没意义的。注:而 BN 应用在 CNN 可以的原因是同一个 channel 的特征图都是由同一个卷积核产生的。
LN 原文的说法是:在训练时,对 BN 来说需要保存每个 step 的统计信息(均值和方差)。在测试时,由于变长句子的特性,测试集可能出现比训练集更长的句子,所以对于后面位置的 step,是没有训练的统计量使用的(不过实践中的话都是固定了 max len,然后 padding 的)。
当然还有一种说法是,不同句子的长度不一样,对所有的样本统计均值是无意义的,因为某些样本在后面的 timestep 时其实是 padding。
还有一种说法是(Normalization helps training of quantized lstm.):应用 BN 层的话,每个 timestep 都需要去保存和计算 batch 统计量,耗时又耗力,后面就有人提出 across timestep 去 shared BN 的统计量,这明显不对,因为不同 timestep 的分布明显是不同的。
最后,大家发现 LN 的效果还很不错,比 BN 好,所以就变成 NLP data 里面的 default config 了。

Layer Normalization的原理
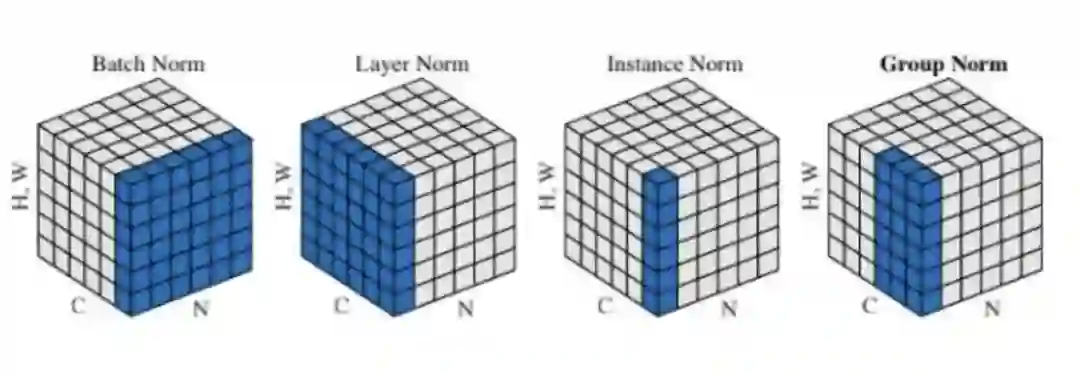
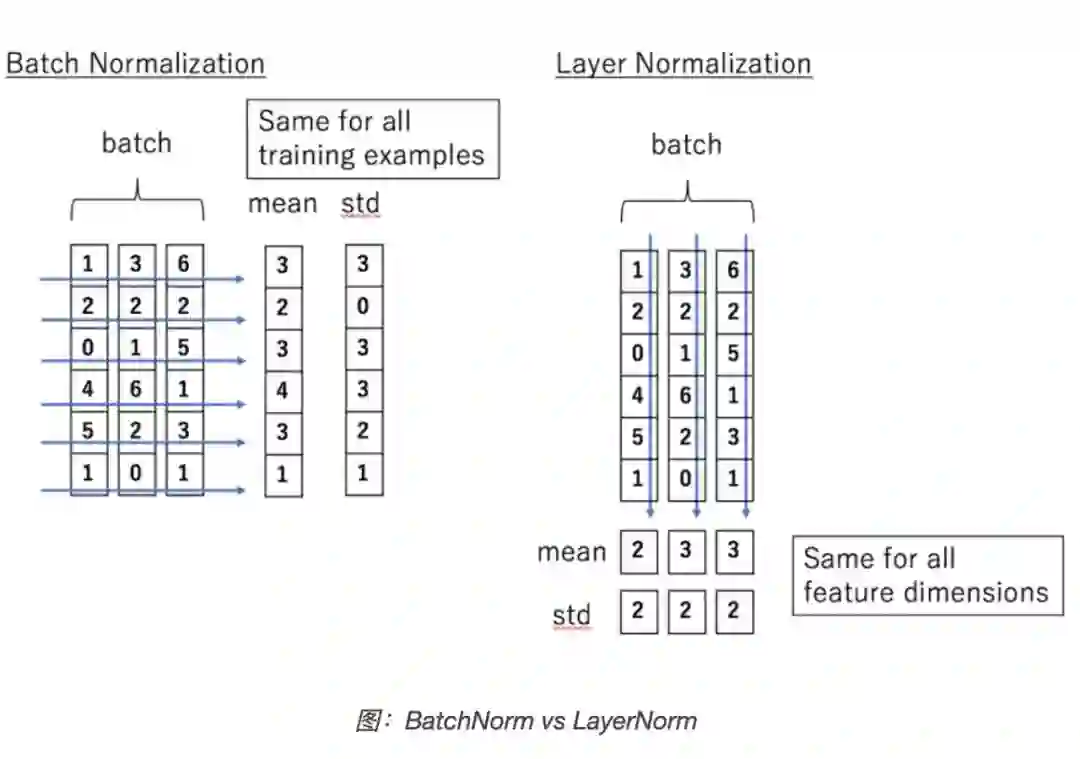
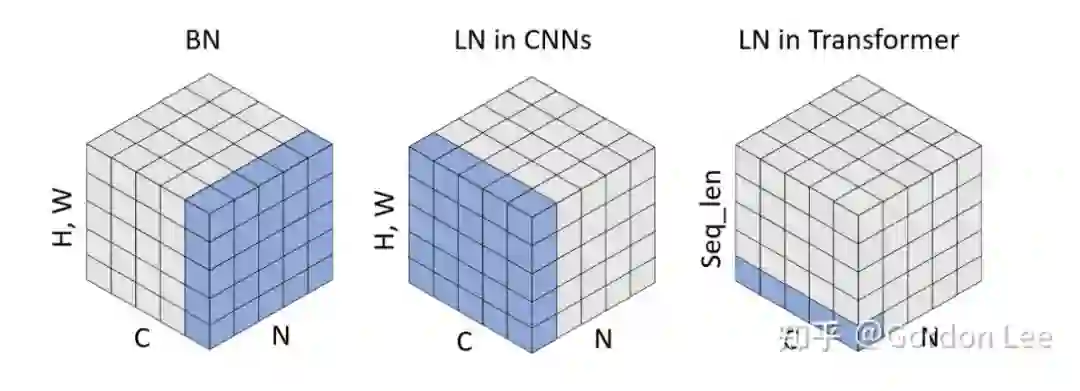
一言以蔽之。BN 是对 batch 的维度去做归一化,也就是针对不同样本的同一特征做操作。LN 是对 hidden 的维度去做归一化,也就是针对单个样本的不同特征做操作。因此 LN 可以不受样本数的限制。
具体而言,BN 就是在每个维度上统计所有样本的值,计算均值和方差;LN 就是在每个样本上统计所有维度的值,计算均值和方差(注意,这里都是指的简单的 MLP 情况,输入特征是(bsz,hidden_dim))。所以 BN 在每个维度上分布是稳定的,LN 是每个样本的分布是稳定的。
# 计算均值和方差
x = torch.randn(bsz, hidden_dim)
mu = x.mean(dim=1) # 注意!要统计的是每个样本所有维度的值,所以应该是dim=1上求均值
sigma = x.std(dim=1)

Transformer中Layer Normalization的实现
对于一个输入 tensor:(batch_size, max_len, hidden_dim)应该如何应用 LN 层呢?
注意,和 Batch Normalization 一样,同样会施以线性映射的。区别就是操作的维度不同而已!公式都是统一的:减去均值除以标准差,施以线性映射。同时 LN 也有 BN 的那些个好处!
# features: (bsz, max_len, hidden_dim)
#
class LayerNorm(nn.Module):
def __init__(self, features, eps=1e-6):
super(LayerNorm, self).__init__()
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
# 就是在统计每个样本所有维度的值,求均值和方差,所以就是在hidden dim上操作
# 相当于变成[bsz*max_len, hidden_dim], 然后再转回来, 保持是三维
mean = x.mean(-1, keepdim=True) # mean: [bsz, max_len, 1]
std = x.std(-1, keepdim=True) # std: [bsz, max_len, 1]
# 注意这里也在最后一个维度发生了广播
return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
讨论:Transformer 为什么使用 Layer normalization,而不是其他的归一化方法?
当然这个问题还没有啥定论,包括 BN 和 LN 为啥能 work 也众说纷纭。这里先列出一些相关的研究论文。
-
Leveraging Batch Normalization for Vision Transformers -
PowerNorm: Rethinking Batch Normalization in Transformers -
Understanding and Improving Layer Normalization
14.1 Understanding and Improving Layer Normalization
这篇文章主要研究 LN 为啥 work,除了一般意义上认为可以稳定前向输入分布,加快收敛快,还有没有啥原因。最后的结论有:
1. 相比于稳定前向输入分布,反向传播时 mean 和 variance 计算引入的梯度更有用,可以稳定反向传播的梯度(让 梯度的均值趋于 0,同时降低其方差,相当于 re-zeros 和 re-scales 操作),起名叫 gradient normalization(其实就是 ablation 了下,把 mean 和 variance 的梯度断掉,看看效果)。
2. 去掉 gain 和 bias 这两个参数可以在很多数据集上有提升,可能是因为这两个参数会带来过拟合,因为这两个参数是在训练集上学出来的。
注:Towards Stabilizing Batch Statistics in Backward Propagation 也讨论了额外两个统计量:mean和variance的梯度的影响。实验中看到了对于小的batch size,在反向传播中这两个统计量的方差甚至大于前向输入分布的统计量的方差,其实说白了就是这两个与梯度相关的统计量的不稳定是BN在小batch size下不稳定的关键原因之一。
14.2 PowerNorm: Rethinking Batch Normalization in Transformers
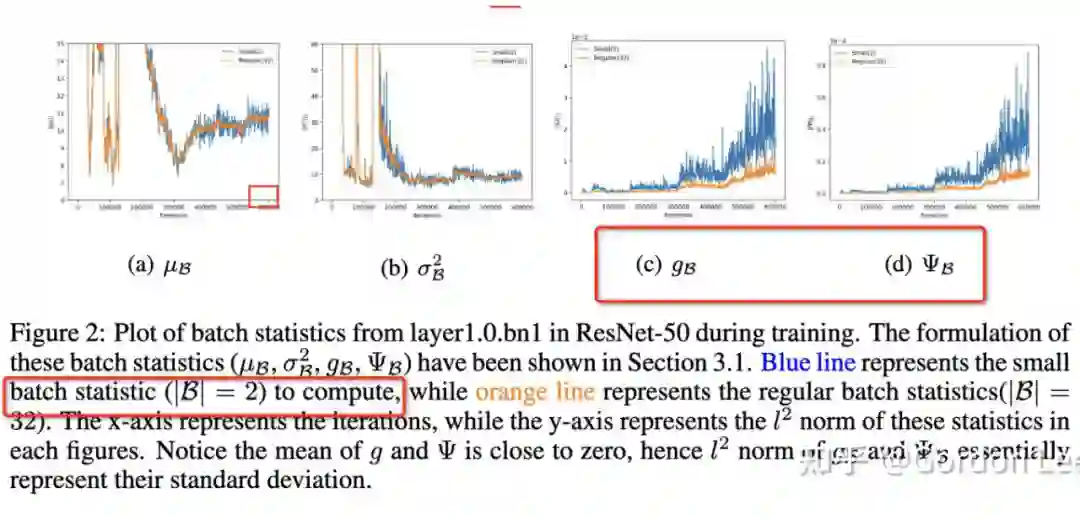
这篇文章就主要研究 Transformer 中 BN 为啥表现不太好。研究了训练中的四个统计量:batch 的均值和方差,以及他们的梯度的均值和方差。对于 batch 的均值和方差,计算了他们和 running statistics(就是用移动平均法累积的均值和方差,见前面的文章)的欧氏距离。可以看到 NLP 任务上(IWSLT14)batch 的均值和方差一直震荡,偏离全局的 running statistics,而 CV 任务也相对稳定。对于他们梯度的均值和方差,研究了其 magnitude(绝对值),可以看到 CV 任务上震荡更小,且训练完成后,也没有离群点。
总结来说,Transformer 中 BN 表现不太好的原因可能在于 CV 和 NLP 数据特性的不同,对于 NLP 数据,前向和反向传播中,batch 统计量及其梯度都不太稳定。
备注:为什么要让mini-batch的statistics拟合running statistics?
来源:Rethinking “Batch” in BatchNorm
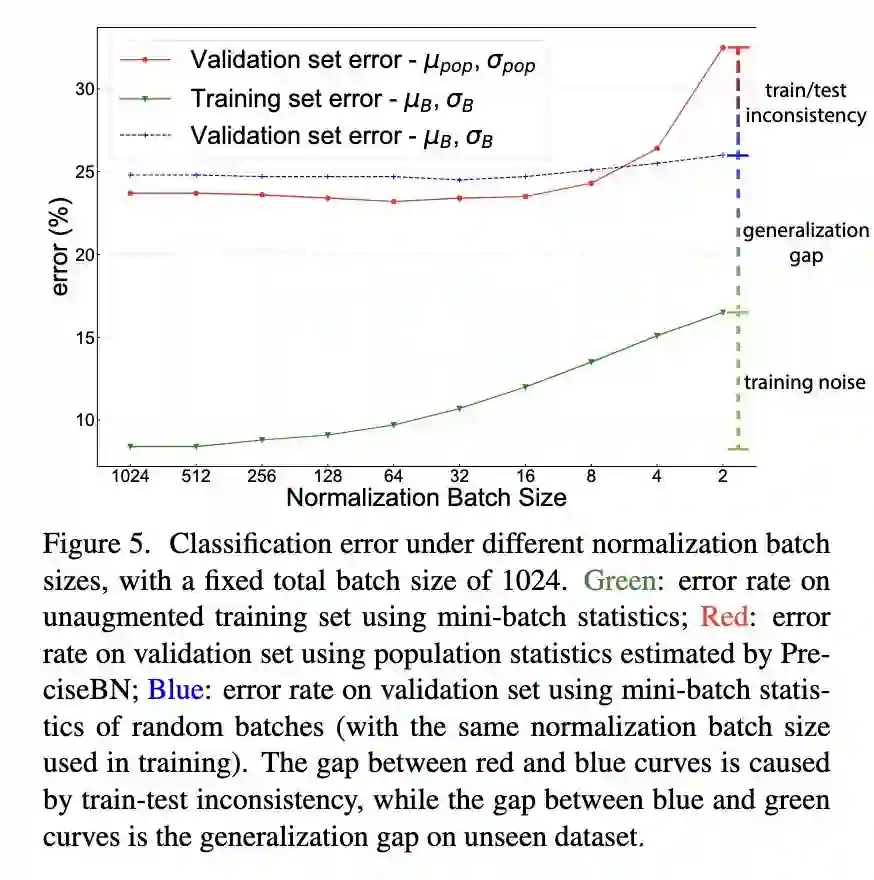
之前的文章讲过,BN 存在训练和测试的不一致的问题,下图表明,在小 batch size 情况下,这种问题很严重,也就是说在 evaluate 时,使用验证集的 mini-batch statisitics 和训练集学到的 population statistics 的差异会大大影响性能。在大 batch size 的时候,这种差异反而会起到正则化的作用。但是一般都是考虑小 batch size 的情况,所以还是希望 batch 的统计量能够尽量接近 running statistics。
14.3 Leveraging Batch Normalization for Vision Transformers
刚刚讲了对于 NLP data,为啥 Transformer 的 BN 表现不好。这篇文章就是去研究对于 CV data,VIT 中能不能用 BN 呢。有一些有意思的观点:
LN 特别适合处理变长数据,因为是对 channel 维度做操作(这里指 NLP 中的 hidden 维度),和句子长度和 batch 大小无关。
BN 比 LN 在 inference 的时候快,因为不需要计算 mean 和 variance,直接用 running mean 和 running variance 就行。
-
直接把 VIT 中的 LN 替换成 BN,容易训练不收敛,原因是 FFN 没有被 Normalized,所以还要在 FFN block 里面的两层之间插一个 BN 层。(可以加速 20% VIT 的训练)。
14.4 其他知友的观点
我个人还是比较同意有个知友的观点:也就是说,对于 NLP data 来说,batch 上去做归一化是没啥意义的,因为不同句子的同一位置的分布大概率是不同的。

总结
Layer Normalization 和 Batch Normalization 一样都是一种归一化方法,因此,BatchNorm 的好处 LN 也有,当然也有自己的好处:比如稳定后向的梯度,且作用大于稳定输入分布。然而 BN 无法胜任 mini-batch size 很小的情况,也很难应用于 RNN。LN 特别适合处理变长数据,因为是对 channel 维度做操作(这里指 NLP 中的 hidden 维度),和句子长度和 batch 大小无关。BN 比 LN 在 inference 的时候快,因为不需要计算 mean 和 variance,直接用 running mean 和 running variance 就行。
BN 和 LN 在实现上的区别仅仅是:BN 是对 batch 的维度去做归一化,也就是针对不同样本的同一特征做操作。LN 是对 hidden 的维度去做归一化,也就是针对单个样本的不同特征做操作。因此,他们都可以归结为:减去均值除以标准差,施以线性映射。对于 NLP data 来说,Transformer 中应用 BN 并不好用,原因是前向和反向传播中,batch 统计量及其梯度都不太稳定。而对于 VIT 来说,BN 也不是不能用,但是需要在 FFN 里面的两层之间插一个 BN 层来 normalized。
参考链接
[1] 月来客栈:模型改善与泛化(标准化与特征映射)https://zhuanlan.zhihu.com/p/139752322
[2] 月来客栈:模型的改善与泛化(梯度与等高线)https://zhuanlan.zhihu.com/p/139756355
[3] 忆臻:为什么梯度的方向与等高线切线方向垂直?https://zhuanlan.zhihu.com/p/27731819
[4] arxiv.org/abs/1805.11604
[5] 神经网络与深度学习https://nndl.github.io/
[6] njustczr:Batch Normalization中的ICS(Internal Covariate Shift)
https://zhuanlan.zhihu.com/p/351669173
[7] 天雨粟:Batch Normalization原理与实战https://zhuanlan.zhihu.com/p/34879333
[8] 海晨威:BN和Dropout在训练和测试时的差别https://zhuanlan.zhihu.com/p/61725100
[9] Batch Normalization在测试和训练阶段的不同https://blog.csdn.net/OliverkingLi/article/details/95970463
[10] 无双谱:从0到1:批量规范化Batch Normalization(实现篇)https://zhuanlan.zhihu.com/p/57847763
[11] BatchNorm的相关细节_爆米花好美啊的博客-CSDN博客https://blog.csdn.net/u013010889/article/details/116522453
[12] How and why does Batch Normalization use moving averages to track the accuracy of the model as it trains?https://stats.stackexchange.com/questions/219808/how-and-why-does-batch-normalization-use-
[13] transformer 为什么使用 layer normalization,而不是其他的归一化方法?https://www.zhihu.com/question/395811291
[14] 为什么Transformer要用LayerNorm?https://www.zhihu.com/question/487766088
[15] Transformer图解 - 李理的博客http://fancyerii.github.io/2019/03/09/transformer-illustrated/
[16] Is it normal to use batch normalization in RNN & LSTM?https://stackoverflow.com/questions/45493384/is-it-normal-to-use-batch-normalization-in-rnn-lstm
[17] https://arxiv.org/pdf/2003.07845.pdf
[18] RNN为什么不适合做BN?https://www.zhihu.com/question/308310065
更多阅读


#投 稿 通 道#
让你的文字被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个,让知识真正流动起来。
📝 稿件基本要求:
• 文章确系个人原创作品,未曾在公开渠道发表,如为其他平台已发表或待发表的文章,请明确标注
• 稿件建议以 markdown 格式撰写,文中配图以附件形式发送,要求图片清晰,无版权问题
• PaperWeekly 尊重原作者署名权,并将为每篇被采纳的原创首发稿件,提供业内具有竞争力稿酬,具体依据文章阅读量和文章质量阶梯制结算
📬 投稿通道:
• 投稿邮箱:hr@paperweekly.site
• 来稿请备注即时联系方式(微信),以便我们在稿件选用的第一时间联系作者
• 您也可以直接添加小编微信(pwbot02)快速投稿,备注:姓名-投稿
△长按添加PaperWeekly小编
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧