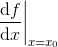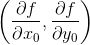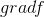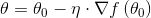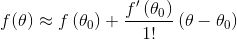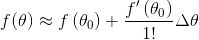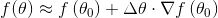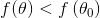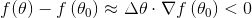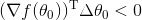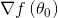面试时让你手推公式不在害怕

面试时让你手推公式不在害怕 | 梯度下降

2019 年 3 月 27 日 计算机视觉life

点“计算机视觉life”关注，置顶更快接收消息！

前面手推公式，后面代码练习
本文阅读时间约10分钟

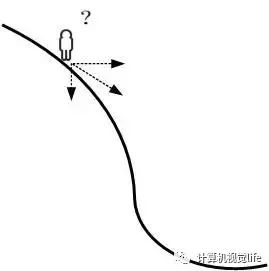
假设这样一个场景，你站在山坡的某个位置，如下图，由于你不知道下山的方向，你需要如何走才能保证安全快速下山呢？用常识来解决这个问题，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后往下走，然后每走一段距离，都反复采用上述方法，最后就能成功的抵达山谷。

梯度下降的基本过程就和下山的场景很类似。还记得上一篇《面试时让你手推公式不在害怕_线性回归》中我们去推导了线性回归的损失函数。并给出两种参数求解方法，一种是求导法一种是梯度下降法。今天我们就来推导一下梯度下降法。首先理解一下什么叫梯度。

梯度

首先看一眼百度百科定义：梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

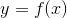
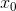
一元函数在处的梯度是

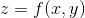
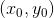
二元函数在处的梯度是：

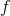
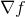
简而言之，对多元函数的各个自变量求偏导数，并把求得的这些偏导数写成向量的形式，就是梯度。我们常把函数的梯度简记为：或

梯度下降公式

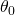
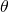
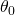
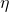
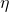
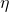
这个公式我们应该比较熟悉。其中，是自变量参数，即当前位置坐标，是更新后的，即下山移动一小步之后的位置。是步长（学习率）即下山的一步大小，如果太小，那么梯度下降的过程缓慢，求解过程慢，如果太大，可能会导致求解过程发散，无法收敛到最优解。

梯度下降算法的公式非常简单！但是为什么局部下降最快的方向就是梯度的负方向呢？也许很多朋友还不太清楚。没关系，接下来我将以通俗的语言来详细解释梯度下降算法公式的数学推导过程。

梯度下降推导

一元函数的泰勒展开大家应该都知道，公式如下：

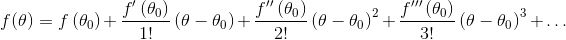
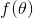
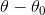
泰勒展开式利用的就是函数的局部线性近似这个概念，主要利用的数学思想就是曲线函数的线性拟合近似。不妨只取右边式子的前两项，很容易得到的近似表达式（可以这样认为很小，相对于整个山的高度，你迈出的一小步，真的很小，这样就可以忽略二次及更高项）为：

记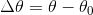：，上式变为：

由于我们上面讲过一元函数的导数就是他的梯度，即上式可以写成：

因为我们是一个下山问题，也就是说希望迭代过程中函数值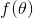会逐渐减小，用数学语言描述就是：

这样我们问题就转变为：

即，如果推广为多元函数即要保证

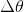
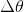
这个公式非常重要，只要我们能保证上式成立，就可以保证函数值下降。有无穷个方向，即可以有无穷个方向下山，那我们该怎么取才能保证上式成立呢？

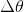
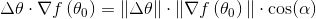
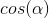
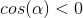
还记得我们上面说过梯度是个向量，是个向量，那两个向量的乘积是，其中是两个向量的夹角，因为两个向量的模乘积大于0，只要就能保证上面式子成立。

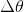
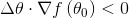
由于对于当前位置梯度是固定的所以只要选择合适的，就能保证成立。

因为我们想快速下山，那就要保证两个向量夹角最小，即时取极小值-1，所以

是一个较小的系数，为什么要有这个系数呢，因为泰勒展开式成立的条件是要非常小。

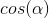
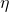
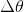
这时候我们就得出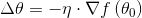，即

只要没有到达梯度为0的点，函数值就会不断减小，实际算法实现时，会选择一个极小的阈值，而不是0。

梯度下降方法对比

批量梯度下降法（Batch Gradient Descent，BSD）：每次更新考虑所有样本，较容易求最优解，算法速度慢。

随机梯度下降法（stochastic gradient descent，SGD）：每次一个样本更新，迭代速度快，但不一定向着目标方向运动，容易陷入局部最优解。

小批量梯度下降法（Mini-batch Gradient Descent）：每次选择一部分样本进行更新，（属于在唱歌的里面相声说的最好，说相声的里面唱歌最棒类型）速度比BSD快，比SGD慢；精度比BSD低，比SGD高。

梯度下降方法可能遇到的问题

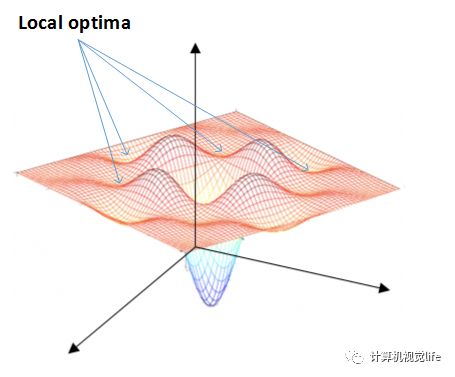
由之前我们公式推导其实可以看出，算法遇到梯度为零的情况下，就会结束迭代，我们只是假设只存在一个全局最小值点梯度为零，而现实中，可能存在局部最小值或者鞍点造成算法失效，因为鞍点和局部最小值梯度同样为零，参照下面的展示图，如果梯度下降求解时遇到鞍点或者局部最小值，会造成算法误认为找到全局最优解而停止迭代，对于如何避免上述问题，有一些解决方案，这里并不展开阐述，以后有机会专门写文章阐述。

1)鞍点（saddle point）

2）局部最小值（local minima）

代码实现

1.分类机器学习肯定很容易想起Scikit-learn包，详情参照文档，网址：http://sklearn.apachecn.org/#/docs/6其中SGDClassifier 类实现了一个简单的随机梯度下降学习例程, 支持不同的 loss functions（损失函数）和 penalties for classification（分类处罚）。我们简单看一个官方例子：

from sklearn.linear_model import SGDClassifierfrom sklearn.datasets.samples_generator import  make_blobsX,y = make_blobs(n_samples=50,centers=2,random_state=0,cluster_std=0.6)clf = SGDClassifier(loss='hinge',alpha=0.01,max_iter=200,fit_intercept=True)clf.fit(X,y)print("回归系数：",clf.coef_)print("偏差",clf.intercept_)

（左右滑动查看）

具体的 loss function（损失函数）可以通过 loss 参数来设置。 SGDClassifier 支持以下的 loss functions（损失函数）：

loss="hinge": (soft-margin) linear Support Vector Machine （（软-间隔）线性支持向量机），

loss="modified_huber": smoothed hinge loss （平滑的 hinge 损失），

loss="log": logistic regression （logistic 回归），

and all regression losses below（以及所有的回归损失）。

2.回归SGDRegressor 类实现了一个简单的随机梯度下降学习例程，它支持用不同的损失函数和惩罚来拟合线性回归模型。

from sklearn import linear_modelfrom sklearn.datasets import load_bostonX,y = load_boston().data,load_boston().targetclf = linear_model.SGDRegressor(loss='squared_loss',penalty='l2',alpha=0.01,max_iter=100)clf.fit(X, y)print('得分：',clf.score(X,y))print('回归系数：',clf.coef_)print('偏差：',clf.intercept_ )

（左右滑动查看）

loss="squared_loss": Ordinary least squares（普通最小二乘法）,

loss="huber": Huber loss for robust regression（Huber回归）,

loss="epsilon_insensitive": linear Support Vector Regression（线性支持向量回归）.

这可能是「多模态机器学习」最通俗易懂的介绍