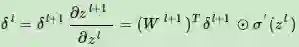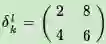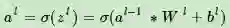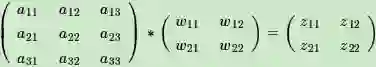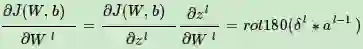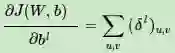干货 | 深度学习之CNN反向传播算法详解

会员服务 ·

干货 | 深度学习之CNN反向传播算法详解

2017 年 11 月 21 日 机器学习算法与Python学习

微信公众号

关键字全网搜索最新排名

【机器学习算法】：排名第一

【机器学习】：排名第一

【Python】：排名第三

【算法】：排名第四

前言

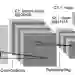
在卷积神经网络(CNN)前向传播算法（干货 | 深度学习之卷积神经网络（CNN）的前向传播算法详解）中对CNN的前向传播算法做了总结，基于CNN前向传播算法的基础，下面就对CNN的反向传播算法做一个总结。在阅读本文前，建议先研究DNN的反向传播算法：深度神经网络（DNN）反向传播算法(BP)（深度学习之DNN与反向传播算法）

DNN反向传播

首先回顾DNN的反向传播算法。在DNN中，首先计算出输出层的δL:

利用数学归纳法，用δl+1的值一步步的向前求出第l层的δl，表达式为：

有了δl的表达式，从而求出W,b的梯度表达式：

有了W,b梯度表达式，就可以用梯度下降法来优化W,b,求出最终的所有W,b的值。现在想把同样的思想用到CNN中，很明显，CNN有些不同的地方，不能直接去套用DNN的反向传播算法的公式。

CNN反向传播思想

要套用DNN的反向传播算法到CNN，有几个问题需要解决：

1）池化层没有激活函数，这个问题倒比较好解决，我们可以令池化层的激活函数为σ(z)=z，即激活后就是自己本身。这样池化层激活函数的导数为1.

2）池化层在前向传播的时候，对输入进行了压缩，那么我们现在需要向前反向推导δl−1，这个推导方法和DNN完全不同。

3) 卷积层是通过张量卷积，或者说若干个矩阵卷积求和而得的当前层的输出，这和DNN很不相同，DNN的全连接层是直接进行矩阵乘法得到当前层的输出。这样在卷积层反向传播的时候，上一层的δl−1递推计算方法肯定有所不同。

4）对于卷积层，由于W使用的运算是卷积，那么从δl推导出该层的所有卷积核的W,b的方式也不同。

从上面可以看出，问题1比较好解决，而问题2,3,4也是解决CNN反向传播算法的关键所在。另外要注意到的是DNN中的al,zl都只是一个向量，而我们CNN中的al,zl都是一个三维的张量，即由若干个输入的子矩阵组成。

下面我们就针对问题2,3,4来一步步研究CNN的反向传播算法。在研究过程中，需要注意的是，由于卷积层可以有多个卷积核，各个卷积核的处理方法是完全相同且独立的，为了简化算法公式的复杂度，我们下面提到卷积核都是卷积层中若干卷积核中的一个。

已知池化层δl，求上一隐藏层δl−1

首先解决上面的问题2，如果已知池化层的δl，推导出上一隐藏层的δl−1。在前向传播算法时，池化层一般我们会用MAX或者Average对输入进行池化，池化的区域大小已知。现在我们反过来，要从缩小后的误差δl，还原前一次较大区域对应的误差。

在反向传播时，首先会把δl的所有子矩阵矩阵大小还原成池化之前的大小，然后如果是MAX，则把δl的所有子矩阵的各个池化局域的值放在之前做前向传播算法得到最大值的位置。如果是Average，则把δl的所有子矩阵的各个池化局域的值取平均后放在还原后的子矩阵位置。这个过程一般叫做upsample。

用一个例子可以很方便的表示

假设池化区域大小是2x2。δl的第k个子矩阵为:

由于池化区域为2x2，我们先讲δkl做还原，即变成：

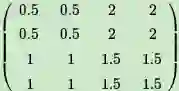
如果是MAX，假设之前在前向传播时记录的最大值位置分别是左上，右下，右上，左下，则转换后的矩阵为：

如果是Average，则进行平均：转换后的矩阵为：

进而

其中，upsample函数完成了池化误差矩阵放大与误差重新分配的逻辑。

已知卷积层δl，求上一隐藏层δl−1

对于卷积层的反向传播，首先回忆下卷积层的前向传播公式：

在DNN中，我们知道δl−1和δl的递推关系为：

这里的式子其实和DNN的类似，区别在于对于含有卷积的式子求导时，卷积核被旋转了180度。即式子中的rot180()，翻转180度的意思是上下翻转一次，接着左右翻转一次。在DNN中这里只是矩阵的转置。那么为什么呢？由于这里都是张量，直接推演参数太多了。以一个简单的例子说明这里求导后卷积核要翻转。

假设l−1层的输出al−1是一个3x3矩阵，第l层的卷积核Wl是一个2x2矩阵，采用1像素的步幅，则输出zl是一个2x2的矩阵。我们简化都是bl都是0,则有

列出a,W,z的矩阵表达式如下：

利用卷积的定义，很容易得出：

接着我们模拟反向求导：

为了符合梯度计算，在误差矩阵周围填充了一圈0，此时将卷积核翻转后和反向传播的梯度误差进行卷积，就得到了前一次的梯度误差。这个例子直观的介绍了为什么对含有卷积的式子求导时，卷积核要翻转180度的原因。

已知卷积层δl，推导该层W,b梯度

现在已经可以递推出每一层的梯度误差δl了，对于全连接层，可以按DNN的反向传播算法求该层W,b的梯度，而池化层并没有W,b,也不用求W,b的梯度。只有卷积层的W,b需要求出。注意到卷积层z和W,b的关系为：

因此有：

由于有上一节的基础，大家应该清楚为什么这里求导后要旋转180度了。而对于b,则稍微有些特殊，因为δl是三维张量，而b只是一个向量，不能像DNN那样直接和δl相等。通常的做法是将δl的各个子矩阵的项分别求和，得到一个误差向量，即为b的梯度：

CNN反向传播总结

现在总结下CNN的反向传播算法，以最基本的批量梯度下降法为例来描述反向传播算法。

输入：m个图片样本，CNN模型的层数L和所有隐藏层的类型，对于卷积层，要定义卷积核的大小K，卷积核子矩阵的维度F，填充大小P，步幅S。对于池化层，要定义池化区域大小k和池化标准（MAX或Average），对于全连接层，要定义全连接层的激活函数（输出层除外）和各层的神经元个数。梯度迭代参数迭代步长α,最大迭代次数MAX与停止迭代阈值ϵ

输出：CNN模型各隐藏层与输出层的W,b