可视化推导贝叶斯定理公式

↑ 点击 蓝字  关注极市平台

来源丨DeepHub IMBA

编辑丨极市平台

极市导读

 

本文通过可视化的方法对贝叶斯定理进行解释，并引入一个复杂的例子对其进行讲解。 >>加入极市CV技术交流群，走在计算机视觉的最前沿

什么是贝叶斯定理?

在统计和应用数学中，贝叶斯定理也被称为贝叶斯规则，它是一个用于确定事件的偶然性概率的数学公式。贝叶斯定理描述了由事件相关条件的先验知识支持的事件发生的概率。

这个定理以英国统计学家贝叶斯的名字命名，他在1763年发现了这个公式。它被认为是被称为贝叶斯推断的特殊统计推断方法的灵感。

除了统计学之外，贝叶斯定理还被用于医学和药理学等各个学科。该理论通常用于多个金融领域。例如模拟向借款人贷款的风险或预测投资成功的可能性。

解释

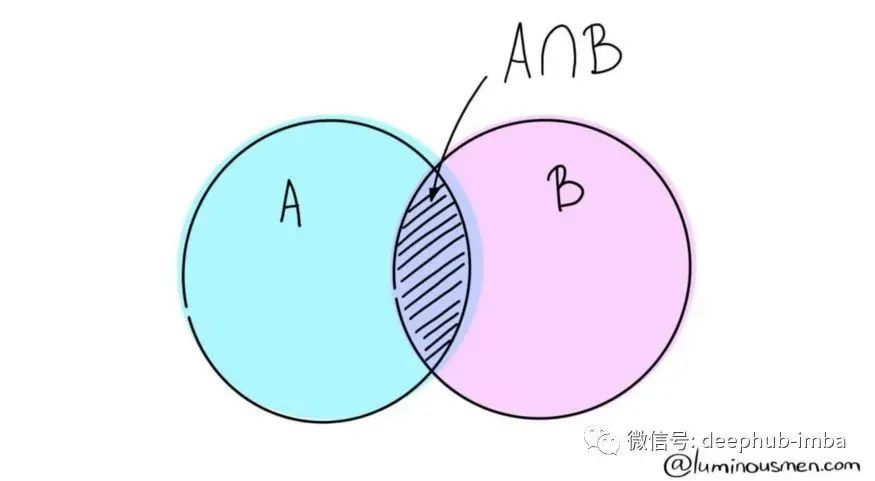
在上面的图片中，我们有两个重叠的事件A和B.例如，A-我今天被弄湿了，B-今天会下雨。在一种或另一种方法中，许多事件彼此关联，如我们的示例中所示。只要B已经发生，让我们计算A的概率。因为B发生了，所以阴影部分是对A重要的也就是是A∩ B、 所以，给定B的概率似乎是：

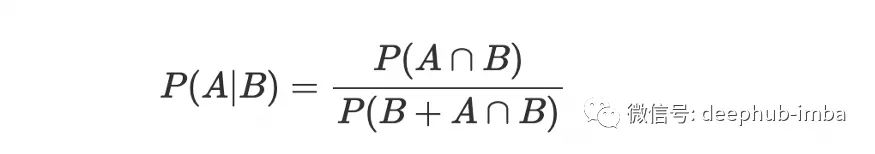
因此，如果 A 已经发生，我们可以写出事件 B 的公式：

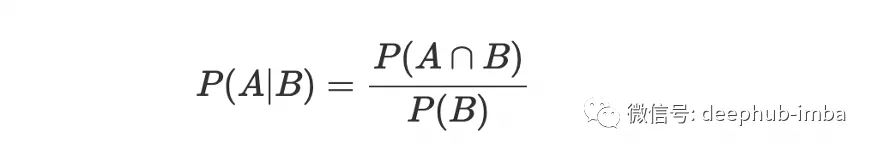
或者：

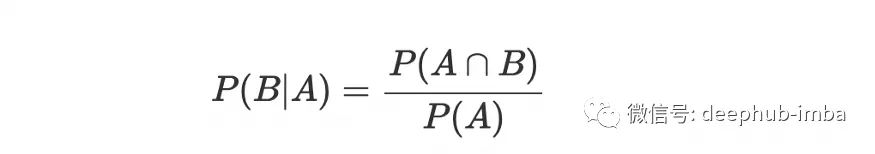
现在，第二个公式可以改写为：

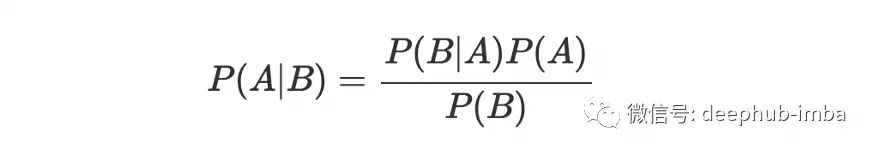
这就是贝叶斯定理公式

其中：

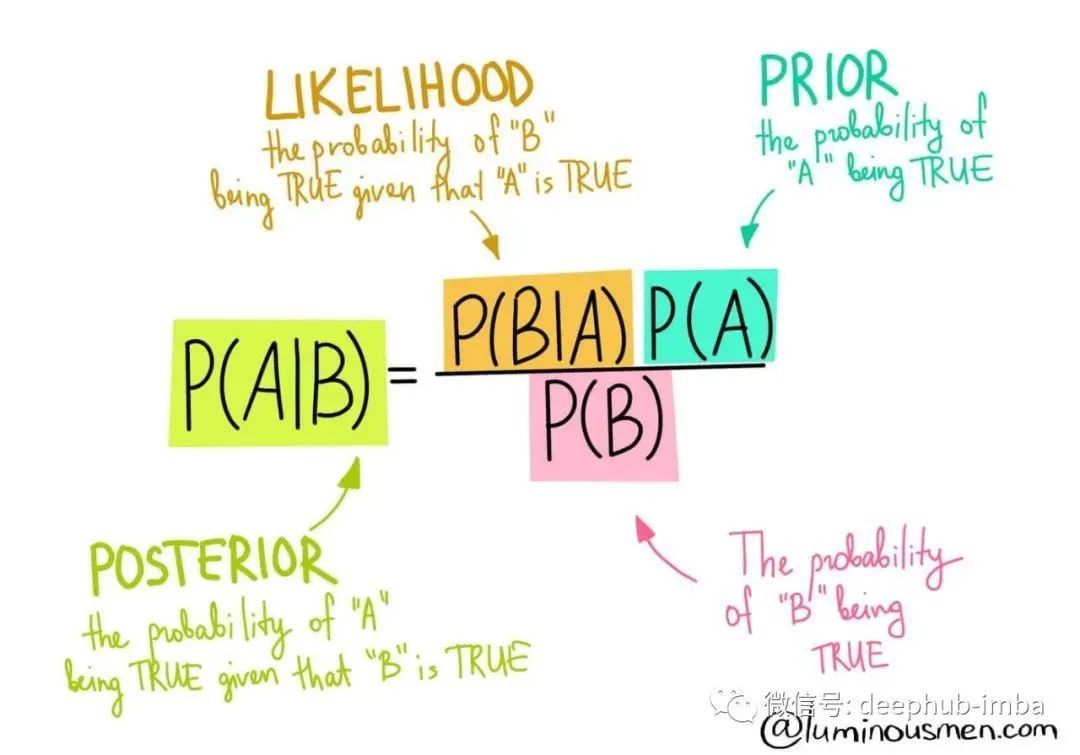
P(A|B) — 给定事件 B 已经发生时事件 A 发生的概率。P(B|A) — 给定事件 A 已经发生时事件 B 发生的概率。

P(A) — 事件 A 单独发生的概率。P(B) — 事件 B 单独发生的概率。

贝叶斯定理的例子

假设您是一家投资银行的证券分析师。与你对上市公司的研究一致，在过去三年内股价上涨了 5% 的企业中，有 60% 的企业在此期间更换了 CEO。与此同时，同期股价涨幅未达到5%的企业中，只有35%更换了CEO。知道股票价格在 4% 中上涨 5% 的概率，找出解雇 CEO 的公司的股票将增加 5% 的概率。

在找到概率之前，必须首先定义概率的表示法。P(A) — 股价上涨 5% 的概率。

P(B) — CEO 被替换的概率。

P(A|B) — 假设 CEO 已被更换，股价上涨 5% 的概率。

P(B|A)——考虑到股价上涨 5%，CEO 更换的概率。

使用贝叶斯定理，我们将找到指定的概率：

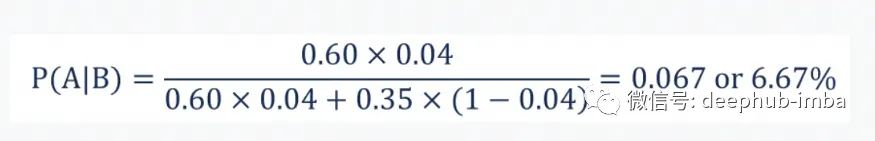
因此，更换 CEO 的公司的股票增长 5% 的概率为 6.67%。

可视化讲解复杂案例

上面的例子很简单，但是为了更好的理解，下面使用一个复杂的例子可视化推理贝叶斯公式：

一家工厂使用三台机器（A、B 和 C）生产产品，它们分别占其产量的 20%、30% 和 50%。在机器 A 生产的产品中，有 5% 是有缺陷的；同样，机器 B 的 3% 的物品和机器 C 的 1% 有缺陷。如果随机选择的物品有缺陷，它是由机器 A 生产的概率是多少？

让我们先画出这个场景的视觉表现：

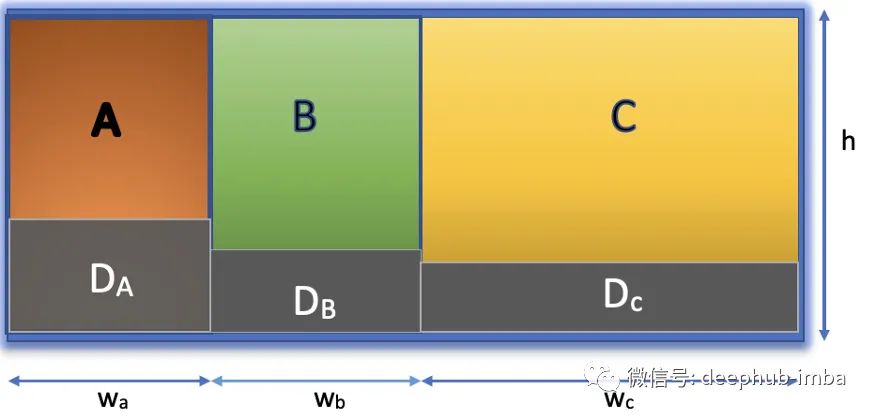
在上述场景中，我们的样本空间 U 由给定工厂生产的所有物品组成，并由图中的外部矩形边界表示。矩形 A、B 和 C 代表机器 A、B 和 C 生产物品的事件，Da、Db 和 Dc 分别代表 A、B 和 C 生产的物品有缺陷的事件。

此外，我假设矩形 U 的高 h=1所以使用我们的面积，Area(U) = 1。

那么我们有，

wa + wb + wc = 1                                                 (1)

同样根据我们的面积假设，机器 A 生产的物品数量与矩形 A 的面积成正比，即

机器A生产的物品数量 =Area(A)

因此，根据概率的定义，机器 A 生产物品的概率，P(A) = 机器生产的物品数量 A ÷ 生产的物品总数，

P(A) = Area(A)/Area(U)

因为Area(U) = 1

P(A) = Area(A) = wa * h = wa                                     (2)

相似地，

P(B) = wb ,P(C) = wc

P(Da) = Area(Da),P(Db) = Area(Db) , P(Dc) = Area(Dc)

如果我们分别取这些矩形 D 的高度为 ha、hb 和 hc，那么P(Da) = wa * ha ，其他也类似。

假设我们知道A已经发生的场景，那么样本空间就变成

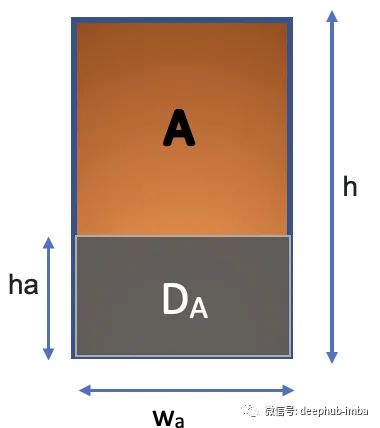
现在给定 A 发生 D 的概率将由下式给出

P(D|A) = Area(Da)/Area(A)
或者
P(D|A) = wa*ha/wa*h

这样

P(D|A) = ha/h                                                           (3)

现在我们考虑场景的第二部分，即假设从样本空间 U 中随机抽样的项目有缺陷。在这种情况下，我们的样本空间现在将缩小到上图中的灰色阴影区域，由矩形 Da、Db 和 Dc 组成，因为缺陷项目只能属于该区域。我们的新样本空间现在的样子如下：

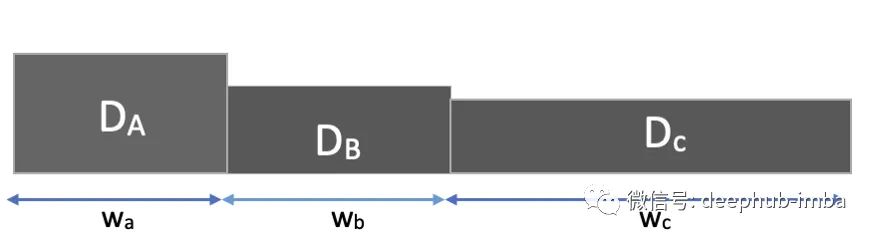
如果现在我们必须找出概率 P(A|D)，即给定缺陷产品来自机器 A 的概率，我们很容易看出这可以用面积写成

P(A|D) = Area(Da) / (Area(Da) + Area(Db) + Area(Dc))

如果我们将分子和分母都除以Area(U) =1，我们得到

P(A|D) = Area(Da)/Area(U) / (Area(Da)+Area(Db)+Area(Dc))/ Area(U)

其中Area(Da)/Area(U) 是 P(Da)，分母项是 P(D) 。

所以我们得到

P(A|D) = P(Da)/P(D)                                              (4)

我们假设矩形 Da 的高度是 ha ，那么

P(Da) = Area(Da) = wa * ha

将项除以 h，矩形 U（或 A）的高度，

P(Da) = (wa * ha * h)/h
或
P(Da) = wa * (ha/h) //  h=1删除了

现在从上面的等式（2），我们知道 wa = P(A)，等式（3），ha/h = P(D|A)。

所以将这些代入等式（2）我们得到

P(A|D) = P(D|A) x P(A) / P(D)

这是不是跟贝叶斯公式一样了

请注意，尽管我对样本空间和区域做了一些假设，但在现实世界的场景中，总是可以像这样表示我们的实验，其中随机事件的形状或区域表示它们的概率。我实际上是从使用概率估计面积的蒙特卡洛方法中获得了这个想法，并将其颠倒过来以使用面积来表示概率。

如果觉得有用，就请分享到朋友圈吧！

△点击卡片关注极市平台，获取 最新CV干货

公众号后台回复“transformer”获取最新Transformer综述论文下载～

极市干货

课程/比赛： 珠港澳人工智能算法大赛 ｜保姆级零基础人工智能教程

算法trick ： 目标检测比赛中的tricks集锦 ｜ 从39个kaggle竞赛中总结出来的图像分割的Tips和Tricks

技术综述： 一文弄懂各种loss function ｜ 工业图像异常检测最新研究总结（2019-2020）

# CV技术社群邀请函 #

△长按添加极市小助手

添加极市小助手微信（ID : cvmart4）

备注：姓名-学校/公司-研究方向-城市（如：小极-北大-目标检测-深圳）

即可申请加入极市目标检测/图像分割/工业检测/人脸/医学影像/3D/SLAM/自动驾驶/超分辨率/姿态估计/ReID/GAN/图像增强/OCR/视频理解等技术交流群

每月大咖直播分享、真实项目需求对接、求职内推、算法竞赛、干货资讯汇总、与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度等名校名企视觉开发者互动交流~

觉得有用麻烦给个在看啦~