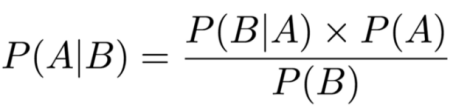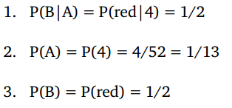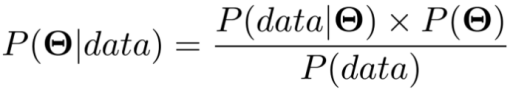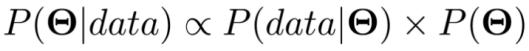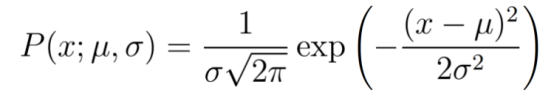概率论之概念解析:用贝叶斯推断进行参数估计
【导读】既昨天推出概率论之概念解析:极大似然估计,大家反响热烈,今天专知推出其续集——贝叶斯推断进行参数估计。本文是数据科学家Jonny Brooks-Bartlett概率论基础概念系列博客中的“贝叶斯推断”一章,主要讲解了使用贝叶斯定理进行参数估计的细节。作者使用简单的例子、通俗的语言讲解枯燥的数学公式,博文内容覆盖了贝叶斯定理、贝叶斯公式、共轭先验、贝叶斯推断进行参数估计。这是一篇非常不错的贝叶斯入门文章,如果你对贝叶斯基础有所欠缺,相信你一定能从本文获益良多。
概率论基础概念系列博客——概率论之概念解析:极大似然估计,阅读专知以前推出的报道:
Probability concepts explained: Bayesian inference for parameter estimation
▌简介
在之前的博文中,我讨论了在机器学习中用极大似然法进行参数估计。这篇文章,我们将介绍另一种参数估计方法,即使用贝叶斯推断进行参数估计。该方法可视为极大似然的一般化方法,在本文中,我也会说明在什么情况下两者方法是等价的。
假设你已经具备了概率论的基本知识。如边缘概率(marginal)和条件(conditional)概率。这些概念在我的系列博文中第一篇已经被介绍过。此外,如果你了解高斯分布,将会有助于理解本文的内容。
▌贝叶斯定理
在介绍贝叶斯推断之前,需要先了解贝叶斯定理。贝叶斯定理允许我们利用已有的知识或者信念(belief)(通常是先验知识prior)帮助我们计算相关事件的概率。例如,如果你想要计算在炎热的晴天卖冰淇淋的概率,就可以使用贝叶斯定理。根据贝叶斯定理,我们可以利用在其他天气(如雨天、多云、下雪天等)销售冰淇淋的可能性作为先验知识,然后计算晴天销售冰淇淋的概率。我们将在下面详细介绍。
▌数学定义
贝叶斯定理公式化表示如下:
其中A和B表示事件,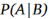
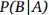
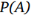
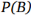
▌示例
单纯的数学公式太抽象了,我们试着举个例子辅助大家理解。给定一副扑克牌,我们从中选择一张卡牌。总共有52张扑克牌(除去大小王),其中有26张红色,26张黑色。抽取一张牌,如果我们已知这张卡牌是红色的,那么这张牌是4的概率是多少?
将上述描述转化成公式化的形式,可以设事件A表示抽取的卡牌是4,事件B表示卡牌是红色。因此,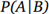
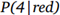
我们可以算出以下概率:
我们用这些已知的概率带入到贝叶斯公式中,得到1/13.
▌贝叶斯定理如何利用先验知识?
我在上文中提及贝叶斯定理可以利用我们的先验知识,下面我们介绍如何使用贝叶斯定理来解决“冰淇淋和天气”的问题。
设事件A表示销售冰淇淋,事件B表示天气。然后我们可能会问,在任何天气下卖冰淇淋的概率是多少?将这个问题公式化表示为:P(A|B)。这与贝叶斯公式等式左侧相等。
等式右侧的P(A)是先验。在我们的例子中,它表示P(A=销售冰淇淋),即不考虑天气的情况下,销售冰淇淋的概率。P(A)之所以是先验,是因为其概率我们是知道的。例如,我可以统计一下,在100人中有30人实际上在某个商店里买了冰淇淋。所以,我不用考虑天气就能知道,P(A=销售冰淇淋)=0.3。贝叶斯理论就是这样考虑先验信息的。
注意:我在上面提到,我可以从统计一个商店的数据来获得先验信息,也可以选择不依赖任何知识的先验。 有人也提出一个根据个人经验和特定领域知识作为先验。但我们需要知道,先验的选择会影响输出结果,我将在后面讨论如先验的强度如何影响输出的结果。
▌贝叶斯推断
定义
目前我们已经了解了贝叶斯定理,并且能够简单使用,然后我们开始讨论贝叶斯推断。
首先,(统计学)推断是从数据中推导一个概率分布性质的过程。我们以前通过极大似然估计来完成这个工作,即给定一系列观测数据点,我们进行极大似然估计得到参数的估计,相当于得到关于数据集中这个参数变量的均值信息。
贝叶斯推断是给定观测数据,利用贝叶斯定理来推导概率分布的性质。
使用分布的贝叶斯定理
上面给出的例子都是在单变量上使用贝叶斯定理方程, 这意味着我们得到的答案也是单个变量值。 但是,有时候单变量并不合适,我们需要考虑多维分布。
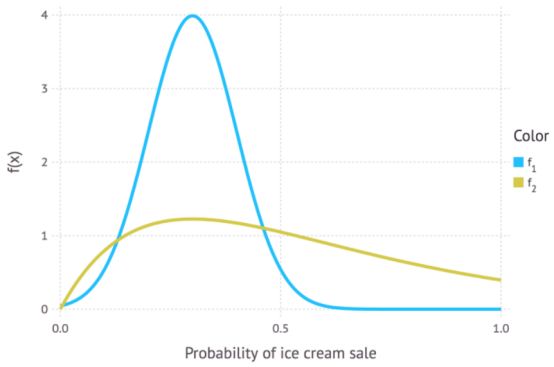
在上面的“冰淇淋”例子中个,我们可以看到“销售冰淇淋”的先验概率是0.3。然而,如果0.3只是一个不确定的猜测呢,先验概率值也有可能是0.25或0.4。这时候,我们就需要把先验当做一个分布来考虑(而不是一个值)。这个分布就叫做先验分布。
上图中的两个分布代表在任何天气中我们的先验分布。蓝色曲线和金色曲线的峰值都在0.3附近,因为我们认为0.3是最可能的先验概率(不排除其他可能性)。事实上,当横坐标不是0.3时,其取值f(x)也不为0. 蓝色曲线表示先验概率取值可能在0-0.5之间任何值,金色曲线表示先验概率取值可能是0-1之间的任何值。从图中可以看出,金色曲线比蓝色曲线更加分散,峰值也更小,这表明金色曲线的先验概率“更加不确定”。
用类似的方式,我们可以用分布表示贝叶斯定理中的其他术语。
▌贝叶斯定理模型
在上面的贝叶斯定理的介绍中,我使用了A和B表示事件。但是在描述贝叶斯模型的时候通常使用不同的符号来表示。
取代符号A,我们通常用Θ表示感兴趣的事件,它表示一组参数。所以,如果你估计高斯分布的参数时,Θ表示高斯分布的均值μ和标准差σ(公式表示为:Θ = {μ, σ})。
取代符号B,我们看到数据y = {y1, y2, …, yn},该符号表示观测数据集。我在等式中使用data来表示数据。
现在,贝叶斯定理可写成如下式子:
上式中,P(Θ)是先验分布,表示我们根据经验对参数值的估计。方程左侧的P(Θ|data)是后验分布。表示我们每次用观测值更新我们的先验分布获得的新的分布。P(data| Θ)表示似然分布,这与我们之前在极大似然估计的章节中讲到的L(data; μ, σ)是类似的,有时也被称为证据(evidence)。这样,我们就可以通过先验分布更新证据(evidence),从而计算出后验分布。
为什么忽略P(data)
因为我们在推断过程中只关心参数值,而P(data)是不含有任何参数的。事实上,P(data)并不参与分布的计算,它只是一个数值。P(data)的值可以通过观测数据获得。一般P(data)的计算是很复杂的,所以现有很多方法都是计算它的。Prasoon Goyal有一篇博客介绍了几种计算方法,链接:
https://medium.com/@prasoongoyal13
P(data)的值是标准化常数,概率分布的一个重要条件就是,其所以可能的值总和为1。标准化常数确保后验分布的所有可能概率值总和为1(或者针对连续概率分布,其表示积分为1).
在某些情况下,我们并不关心分布的性质。我们只关心分布峰值处的概率,不论分布是否标准化。因此,也有很多人把贝叶斯定理写成如下形式:
其中∝表示等式两边成正比。因为我们没有考虑标准化常量P(data),所以等式两边严格来讲并不相等。
▌贝叶斯推断(Bayesian inference)举例
你可能需要一些时间来消化上述理论。让我们继续举个例子,在这个例子中,贝叶斯推理会派上用场。我们的例子是计算氢键(hydrogen bond)的长度。你不需要知道什么是氢键,这只是我在博士期间想出来的一个例子(因为当时我们在生物化学系,所以这个话题跟我们当时的研究很相关)。
图1:我已经把这个图像包括进去了,因为我认为它看起来不错,有助于分解密集的文本,这与我们将要讲的例子是相关的。你不需要理解这个图,因为我们这里讲的是贝叶斯推断的内容。如果你想知道的话,我用Inkscape做这个图。
我们假设一个氢键在3.2Å到4.0Å之间(我从Google中查到这些信息,Ångström,Å,是一个距离单位,1Å等于0.1纳米,所以我们说的是非常小的距离)。这些信息构成我的先验信息。就概率分布而言,我将把它作为一个均值μ=3.6Å和标准偏差σ=0.2Å的高斯分布(见下图)。
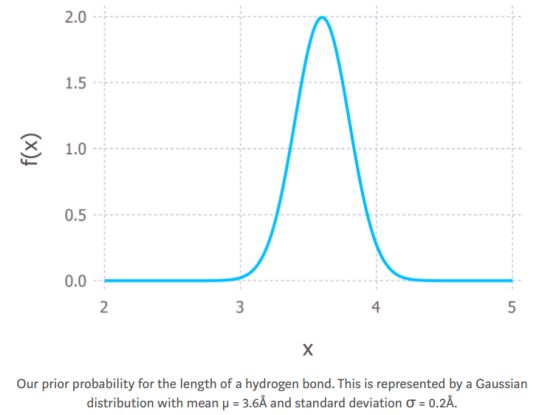
图2:氢键长度的先验概率分布,用高斯分布表示,其均值μ=3.6Å,标准差σ=0.2Å。
现在我们得到一些数据(是从均值为3Å,标准差为0.4Å的高斯分布随机生成的5个数据点,在现实世界中,这些数据从实验中得到),这些数据给出了测量的氢键的长度(图3中的金色的点)。我们可以从数据中推导出似然分布,就像我们在之前的文章中用极大似然的方法一样。 假设这些数据是由一个可以用高斯分布描述的过程生成的,我们得到了下图中金色曲线所代表的似然分布。请注意,这5个数据点的均值的最大似然估计值小于3(约为2.8Å)。
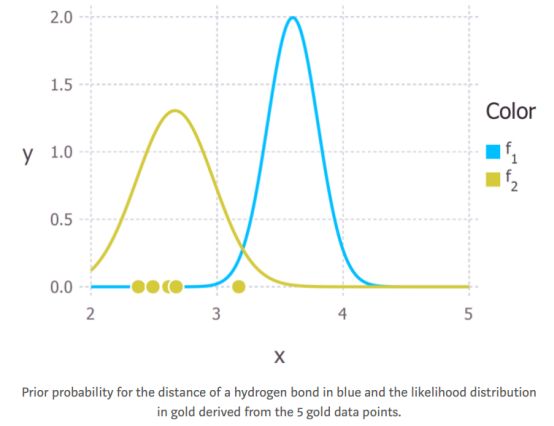
图3:从五个数据点得出的氢键距离的先验概率(蓝色表示)和5个数据点的似然分布(金色表示)
现在我们有两个高斯分布,蓝色代表先验,金色代表似然。我们不关心标准化常数,所以我们可以根据上述两个分布来计算非标准化的正态后验分布。回想一下,表示高斯概率分布的等式是:
所以我们要把它们相乘。我不会在这里讲数学,因为这会对我们要讲的内容造成干扰。 如果你对数学感兴趣,那么你可以参考本文的前两页。由此产生的后验分布如下图所示粉红色的曲线。
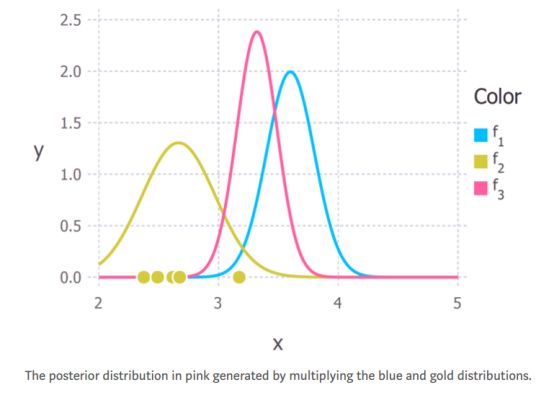
图4:蓝色和金色分布相乘后产生的粉红色曲线就是后验分布。
现在我们有了一个氢键长度的后验分布,我们可以从中得出统计数据。 例如,我们可以利用分布的期望值来估计距离。或者可以计算方差来量化我们对结论的不确定性。后验分布最常见的统计数据之一是mode。这通常被用作估计感兴趣的参数,被称为最大后验概率估计(Maximum a posteriori)或者简单地称为MAP估计。 在这种情况下,后验分布也是高斯分布,所以均值等于mode(和median),而对于氢键距离的MAP估计值在分布峰值处,约为3.2Å。
▌结束语
为什么我总是使用高斯?
为什么我总是使用高斯?你会注意到,在我所有涉及分布的例子中,我都使用了高斯分布。其中一个主要原因是它使数学变得更容易。但是对于贝叶斯推断的例子,它需要计算2个分布的乘积。即使不做数学运算,我也知道后验是高斯分布。这是因为高斯分布有一个特殊的性质,使其易于处理。高斯分布是与高斯似然函数共轭的。这意味着如果我用高斯似然函数乘高斯先验分布,我将得到一个高斯后验函数。后验和先验都来自同一类型的分布(他们都是高斯分布),这被称为共轭分布。在这种情况下,先验分布被称为共轭先验。
在许多推理情况下,我们要恰当地选择似然和先验,使所得的分布是共轭的,因为共轭分布推断更容易。数据科学中的一个例子是潜在狄利克雷分布(Latent Dirichlet Allocation:LDA),它是一种用于在多个文本文档(称为语料库)中查找主题的无监督学习算法。 Edwin Chen的博客对LDA进行了很好的介绍。
当我们获得新的数据会发生什么?
贝叶斯推断的好处之一是它不需要大量的数据。1个观察值就能更新先验。 事实上,贝叶斯框架允许你在数据进入时实时迭代地更新你的beliefs(已有知识)。它的工作原理如下:你对某物(例如参数的值)有一个先验belief,然后接收一些数据。你可以根据上述的介绍来计算后验分布从而更新你的belief。之后,我们得到更多的数据,后验成为了新的先验。我们可以用新数据来更新新的先验,并且再次得到新的后验。这个循环可以无限持续,所以能不断更新你的beliefs。
卡尔曼滤波器(以及它的变体)就是一个很好的例子。它被用在很多情况下,但是可能在数据科学领域最重要的应用是自动驾驶汽车。在我博士(数学蛋白质晶体学)期间,我使用了一种名为无损卡尔曼滤波器(Unscented Kalman Filter)的变体,并代码实现这一算法,也集成到一个开源软件包中。对卡尔曼滤波器的描述可以参考这个博客文章:卡尔曼滤波器是如何工作的,由Tim Babb提供图片。
使用先验作为正则化项(regularisers)
上面估计氢键长度例子中产生的数据表明,2.8Å是最好的估计。但是,如果我们只根据数据做出估计,我们可能会过拟合。如果数据收集过程出了问题,将导致巨大的误差。我们可以在贝叶斯框架中使用先验来解决这个问题。在我们的例子中,使用以3.6Å为均值的先验,结果是一个后验分布,给出的氢键长度的MAP估计为3.2Å。这表明,在估计参数值时,我们的先验可以充当正则化项(regularisers)。
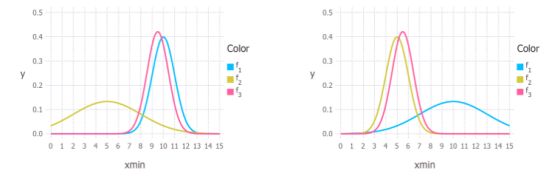
我们在先验和似然性之间的权重值取决于两个分布之间的相对不确定性。在下图中我们可以看到这个图形。颜色与上面相同,蓝色代表先验分布,金色代表似然,后验分布用粉红色表示。在下图左边的图中,你可以看到我们的先验分布的曲线(蓝色)比金色曲线(似然)展开的范围要小得多。所以后验分布更像先验分布。右图中的情况正好相反。
因此,如果我们希望增加参数的正则化,我们可以选择与似然相关性小的先验分布。
MAP估计在什么时候等于极大似然估计?
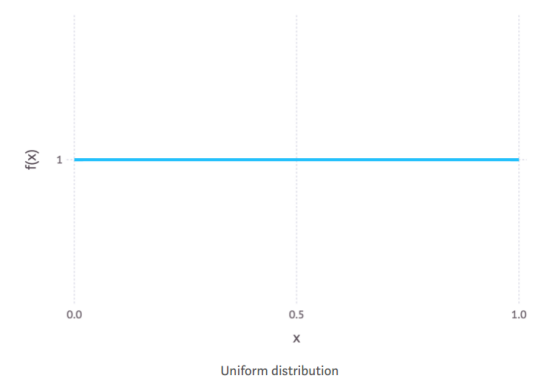
当先验分布为均匀分布时,MAP估计等于MLE(极大似然估计)。下面显示了一个均匀分布的例子。
我们可以看到,均匀分布在x轴上的每个值赋予相等的权重(这是一条水平线)。直观地说,它表示了缺乏先验知识。在这种情况下,所有的权重都被分配给似然函数,所以当我们将先验乘以似然的时候,得到的后验结果非常类似于似然。因此,极大似然法可以看作是MAP的一个特例。
当我开始写这篇文章的时候,我并没有想到会写这么多,非常感谢你们的关注。如果有什么不清楚的地方,或者我在上面的文章中有什么错误,请随时留下评论。在本系列的下一篇文章中,我可能会尝试用P(data)来处理变量消除,这是我在这篇文章中忽略的标准化常量。
谢谢阅读!
原文链接:
https://towardsdatascience.com/probability-concepts-explained-bayesian-inference-for-parameter-estimation-90e8930e5348
Jonny Brooks-Bartlett是知名的数据科学家、演说家;数学家,主页:
https://towardsdatascience.com/@jonnybrooks04?source=post_header_lockup
-END-
专 · 知
人工智能领域主题知识资料查看获取:【专知荟萃】人工智能领域26个主题知识资料全集(入门/进阶/论文/综述/视频/专家等)
同时欢迎各位用户进行专知投稿,详情请点击:
【诚邀】专知诚挚邀请各位专业者加入AI创作者计划!了解使用专知!
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请扫一扫如下二维码关注我们的公众号,获取人工智能的专业知识!
请加专知小助手微信(Rancho_Fang),加入专知主题人工智能群交流!
点击“阅读原文”,使用专知!