【ICLR2022】Transformers亦能贝叶斯推断

目前，贝叶斯方法难以获得深度学习的好处，贝叶斯方法允许对先验知识进行明确的描述，并准确地捕获模型的不确定性。我们提出了先验数据拟合网络(PFNs)。PFNs利用大规模机器学习技术来近似一组大后验。PFNs唯一要求是能够从监督学习任务(或函数)的先验分布中取样。我们的方法将后验逼近的目标重申为带有集值输入的有监督分类问题:它重复地从先前的任务(或函数)中绘制一个任务(或函数)，从中绘制一组数据点及其标签，隐藏其中一个标签，并学习基于其余数据点的集值输入对其进行概率预测。PFNs采用一组新的有监督学习任务的样本作为输入，在学习了近似贝叶斯推理之后，可以对单个正向传播中的任意其他数据点进行概率预测。我们证明PFNs可以近乎完美地模拟高斯过程，也可以对棘手的问题进行有效的贝叶斯推理，与现有方法相比，在多个设置中加速超过200倍。

https://github. com/automl/TransformersCanDoBayesianInference.

在过去的十年中，使用深度学习架构的有监督机器学习(ML)方法在具有大量训练数据的机器学习任务上取得了重大进展(Vaswani et al., 2017; He et al., 2016; Krizhevsky et al., 2012)。因此，ML中的一个非常重要的问题是，将这些成功迁移到可用数据较少的小规模设置任务中。在本文中，我们提出了一种利用深度学习模型建立具有灵活和可替换先验的近似后验模型的方法。它使得指定先验就像定义监督学习任务的抽样方案一样简单。

先验数据拟合网络(PFNs)的可视化。我们从先前的数据集采样，并在这些数据集的保留样本上拟合PFN。给定一个实际的数据集，我们将它和一个测试点输入PFN，并在单个正向传播中获得贝叶斯推理的近似值。

虽然深度学习在大型数据集上的成功可以归因于神经网络近似任何函数的能力，但仍需要对先验知识进行编码，例如通过模型架构(如卷积神经网络(LeCun et al.， 1989))或正则化(如数据增强(Hendrycks et al.，2019;Cubuk et al ., 2020)。另外，没有免费的午餐定理表明没有好的方法来解决这类预测问题(Wolpert & Macready, 1997)。因此，针对不同的小规模任务开发了大量专门的算法(LeCun et al.， 1989;Kadra等人，2021年;Chen & Guestrin, 2016)。然而，将先验信息编码到机器学习模型中可能是一项挑战。

一种明确定义的使模型产生偏差的方法是使用贝叶斯推理。贝叶斯推理的基础是对真实世界应用中出现的数据分布的假设。这一假设产生了对数据遵循特定模型的概率的先验信念。例如，可以实现一个先验，将数据编码为由神经网络(贝叶斯神经网络，(MacKay, 1992))创建的，通过一个多项式，预先定义的编程语言中的高斯混合或随机代码的可能性(Solomonoff, 1997)。在监督学习中使用贝叶斯推理进行预测有以下优点:(1)它有理论基础，使其在先验p(t)符合的情况下有效;(ii)因此可以更好地解释不同事件的实际可能性;(iii)它是很好的校准，(iv)它是可解释的，因为前面描述了模型的期望。然而，在大多数情况下，提取给定先验的后验预测分布是很难的(Blei et al.， 2017;MacKay,1992)。

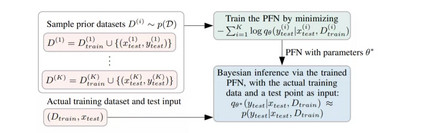
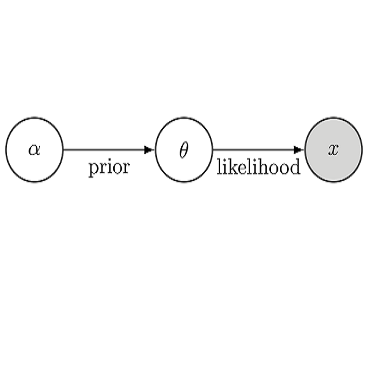
图1概述了先验数据拟合网络(PFNs)，用于近似贝叶斯模型。我们假设在监督学习任务(或函数)上有一个给定的有代表性的先验分布，这就提供了我们的归纳偏差。为了训练PFN，我们使用有监督学习，用集值输入表示整个数据集: 我们从给定的前一个任务中反复取样一个元训练任务(或函数)，从中绘制一组数据点和它们的标签，掩盖其中一个标签，并学习根据其余数据点的集值输入对其进行概率预测。给定一个实际的真实数据集，我们将其与一个测试点作为输入输入PFN，并根据数据集的条件输出测试点的预测分布。正如我们将演示的那样，这种分布近似于贝叶斯后验预测。我们将此步骤称为(贝叶斯)推理，而不是PFN本身的训练。

因此，我们的PFNs 使我们能够近似于我们能够采样数据的任何先验的后验预测分布。与贝叶斯推理的其他近似值的标准假设相比，这是一个非常弱的要求(Hoffman et al., 2014; 2013; Jordan et al., 1999)。这允许对大量先验进行简单的近似，包括当前可用工具很难近似的先验。

我们的贡献如下:

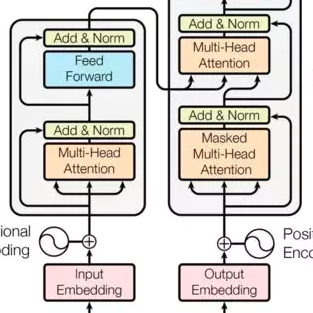
们提出了架构上的变化，成功地使用Transformer进行后验预测分布(PPD)近似，包括一种用于回归任务的新型预测分布。该方法简单、成本低廉，且普遍适用于大先验集。
我们证明PFNs可以比使用NUTS的MCMC或使用Bayes-by-Backprop的SVI更快地逼近高斯过程和贝叶斯神经网络(BNN)的PPD数量级(Blundell等人，2015)。
我们证明PFNs可以对现实世界的任务产生影响。(i)我们在PFN上的架构上使用先验实现BNNs, PFNs允许在单个正向传递中调优自由预测，并在小型表数据集的大型基准测试中优于所有基线。(ii)此外，我们发现，简单的书写可以在Omniglot上实现少样本学习(Lake et al.， 2015)。

成为VIP会员查看完整内容