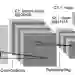
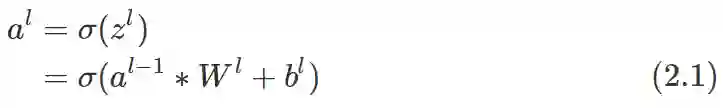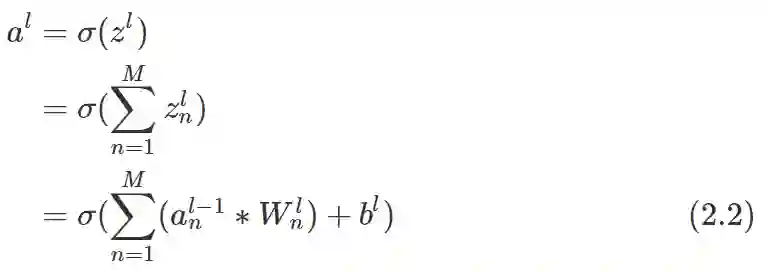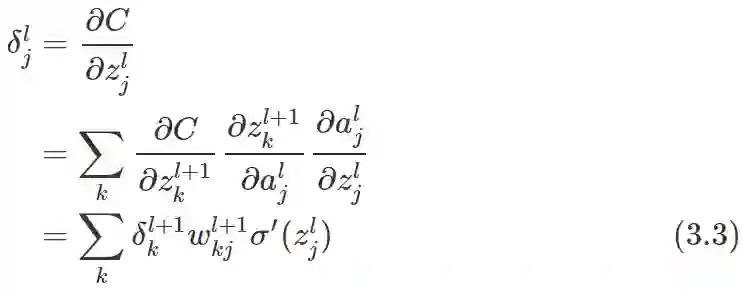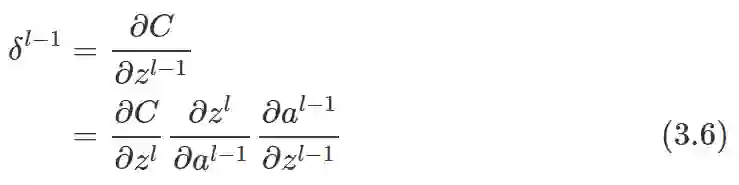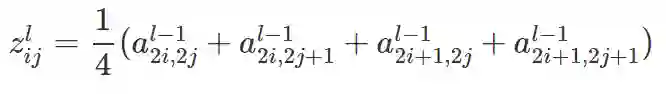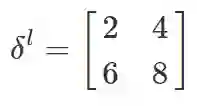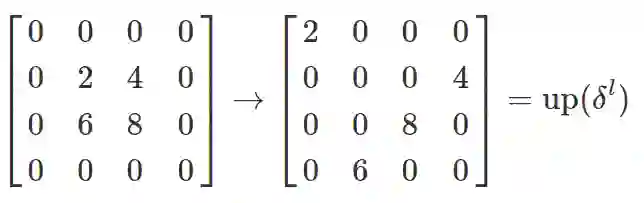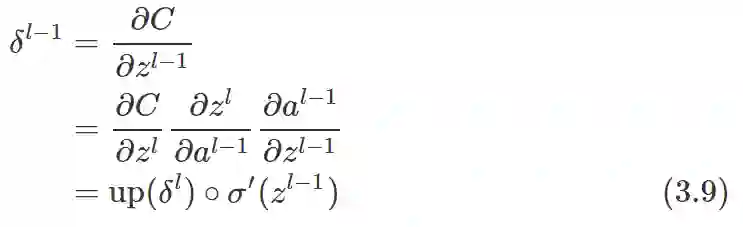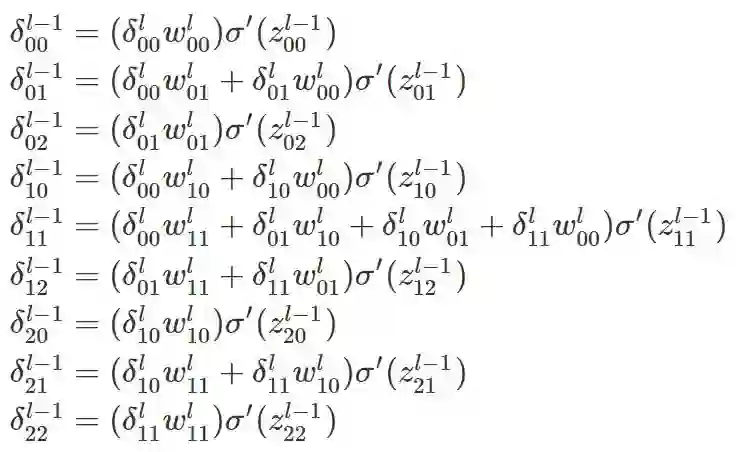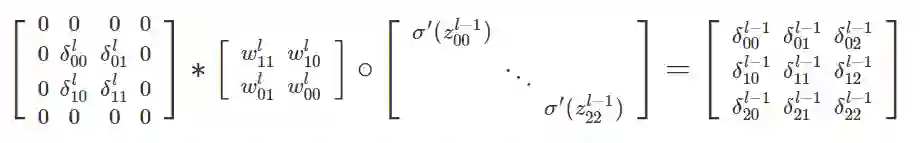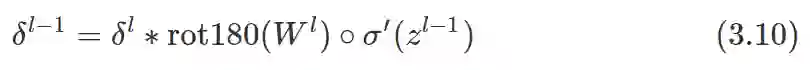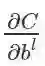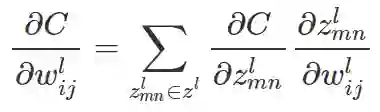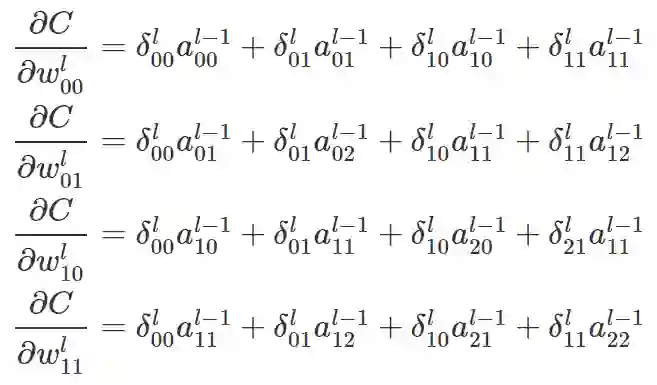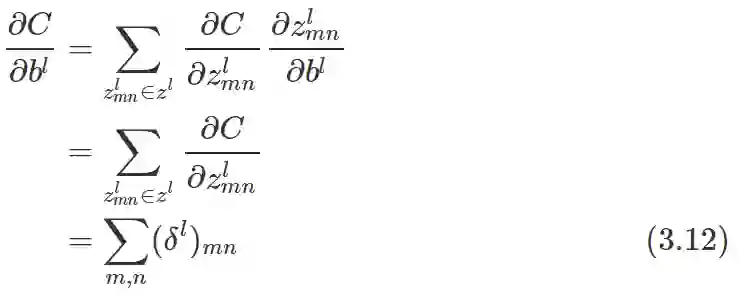CNN 反向传播算法推导

1. CNN 前向传播过程

输入层或隐层前向传播到卷积层 l 的公式如下:

公式中上标表示层数，∗ 表示卷积运算，σ 表示激活函数, 在 CNN 中通常使用 ReLU, b 表示偏置.

当输入图像深度为M时或输入是上一层M个 feature map 的组合时, 上一层前向传播到第 l 层的卷积层的公式可以表示为:

隐层前向传播到池化层 ll 时, 输入的若干矩阵的大小为 M × N, 池化大小是 j × k 的区域, 则所有输出矩阵的维度都为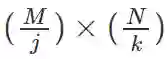. 池化的标准一般为最大池化或平均池化. 这里用 down() 表示池化(下采样)过程. 由于池化层没有激活函数, 则该过程可以用公式表示为:

全连接层间的前向传播公式为:

对于输出层 L:

2. CNN 反向传播算法

2.1 神经网络中的反向传播算法

先回顾一下神经网络反向传播的相关公式.

第 l 层第 j 个神经元的错误量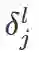为:

输出层中关于错误量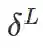的公式:

根据下一层错误量计算错误量的公式:

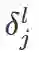
网络的代价函数相对于权重的改变速率的公式:

网络的代价函数相对于偏置的改变速率的公式:

2.2 CNN 反向传播算法推导

这里, 对推导条件进行简化, 只考虑深度为1, 步长为1的情况. 当步长不为1时, 推导过程稍有变化.

(1). 已知池化层误差, 求 l−1 层误差由链式法则可得:

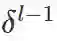
其中,. 那么问题就转化为求.

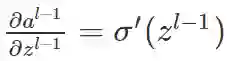
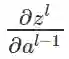
比如, 池化大小为 2 × 2 的区域, 使用平均池化时, 有:

使用最大池化, 有:

可知, 当平均池化大小为 k × k 的区域时, 有:

使用最大池化时, 有:

因此, 可以对池化层的误差矩阵进行上采样操作.

比如, 池化大小为 2 × 2 的区域, 有如下误差矩阵:

若为平均池化, 上采样后每个区域的值为池化层对应的值再乘以, 得:

用克罗内克积表示为:

其中表示克罗内克积,表示按元素相乘.

若为最大池化, 上采样时先将误差矩阵还原, 再将每个区域的误差移动到前向传播时最大值所的位置上. 如记录的位置分别为 (0,0),(1,3),(3,1),(2,2), 则上采样的过程为:

将最大池化形式的误差上采样也表示为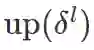, 公式 (3.6) 可写为:

(2). 已知卷积层误差, 求 l−1 层误差

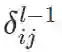
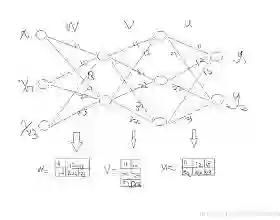
由公式 (3.3) 可知, l−1 层的误差与 l 层中与其相连神经元的误差以及两者间的权重有关. 由于卷积操作是局部感知和权值共享的, 因此误差传播过程和神经网络稍有不同. 考虑如下卷积过程, 输入矩阵的大小为 3×3, 卷积核的大小为 2×2, 输出矩阵的大小为2×2, 标注的 i,j 是元素在矩阵中的位置.

将上图所示卷积过程展开, 并用神经网络神的形式描述. 权重上的标注是其在卷积核中的位置, 相同的权重用同一种颜色表示.

由上图的连接情况可得:

上述9个等式可用矩阵卷积运算表示为:

先在误差矩阵周围填充一圈 0, 然后将卷积核旋转, 两者进行卷积, 再与矩阵按元素相乘, 就得到了前一层的误差矩阵. 用公式表示为:

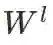
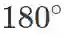
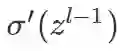
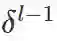
(3). 已知卷积层误差, 求该层和

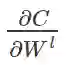
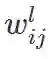
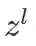
由于任意权重是所有输出的参数, 因此可得:

仍以上述卷积过程为例, 得:

上述等式可用卷积运算表示为:

于是有:

由于偏置 b 也是共享的, 因此在公式 (2.1) 中, 加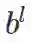的操作是按元素相加的, 可得:

即对误差矩阵中所有元素求和.

参考资料

[1] An Intuitive Explanation of Convolutional Neural Networks, Ujjwal Karn 

链接: https://ujjwalkarn.me/2016/08/11/intuitive-explanation-convnets/

[2] Notes on Convolutional Neural Networks, Jake Bouvrie 

链接: http://cogprints.org/5869/1/cnn_tutorial.pdf

[3] Backpropagation In Convolutional Neural Networks, Jefkine Kafunah 

链接: http://www.jefkine.com/general/2016/09/05/backpropagation-in-convolutional-neural-networks/

[4] 卷积神经网络(CNN)反向传播算法, 刘建平Pinard

链接: https://www.cnblogs.com/pinard/p/6494810.html