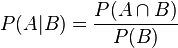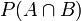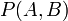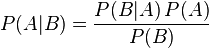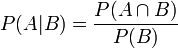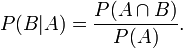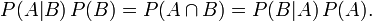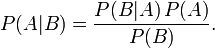面试题：简单说说贝叶斯定理

简单说说贝叶斯定理

解析：

在引出贝叶斯定理之前，先学习几个定义：

1.条件概率（又称后验概率），就是事件A在另外一个事件B已经发生条件下的发生概率。
条件概率表示为P(A|B)，读作“在B条件下A的概率”。
比如，在同一个样本空间Ω中的事件或者子集A与B，如果随机从Ω中选出的一个元素属于B，那么这个随机选择的元素还属于A的概率就定义为在B的前提下A的条件概率。
所以：P(A|B) = |A∩B|/|B|，接着分子、分母都除以|Ω|得到联合概率表示两个事件共同发生的概率。
A与B的联合概率表示为或。

2.边缘概率（又称先验概率），是某个事件发生的概率。
边缘概率是这样得到的：
在联合概率中，把最终结果中那些不需要的事件通过合并成它们的全概率，而消去它们（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率）。
这称为边缘化（marginalization），比如A的边缘概率表示为P(A)，B的边缘概率表示为P(B)。 
接着，考虑一个问题：P(A|B)是在B发生的情况下A发生的可能性。
首先，事件B发生之前，我们对事件A的发生有一个基本的概率判断，称为A的先验概率，用P(A)表示；
其次，事件B发生之后，我们对事件A的发生概率重新评估，称为A的后验概率，用P(A|B)表示；
类似的，事件A发生之前，我们对事件B的发生有一个基本的概率判断，称为B的先验概率，用P(B)表示；
同样，事件A发生之后，我们对事件B的发生概率重新评估，称为B的后验概率，用P(B|A)表示。

贝叶斯定理便是基于下述贝叶斯公式：
上述公式的推导其实非常简单，就是从条件概率推出。
根据条件概率的定义，在事件B发生的条件下事件A发生的概率是
同样地，在事件A发生的条件下事件B发生的概率
整理与合并上述两个方程式，便可以得到：
接着，上式两边同除以P(B)，若P(B)是非零的，我们便可以得到贝叶斯定理的公式表达式：

所以，贝叶斯公式可以直接根据条件概率的定义直接推出：
即因为P(A,B) = P(A)P(B|A) = P(B)P(A|B)，所以P(A|B) = P(A)P(B|A)  / P(B)。

更多请参见此文：《从贝叶斯方法谈到贝叶斯网络》（链接：http://blog.csdn.net/v_july_v/article/details/40984699）。

 

就业班来了

依据个人情况定制化教学

名企面试官亲自辅导面试

让你“薪”满意足！

↓扫码查看课程详情↓

10分钟入门推荐系统，这份有实战、有代码的资料火了！

数学差，连机器学习都做不了吗？（文末送课送电影票！）

戳 “阅读原文”查看课程一起进步！

你在看吗？