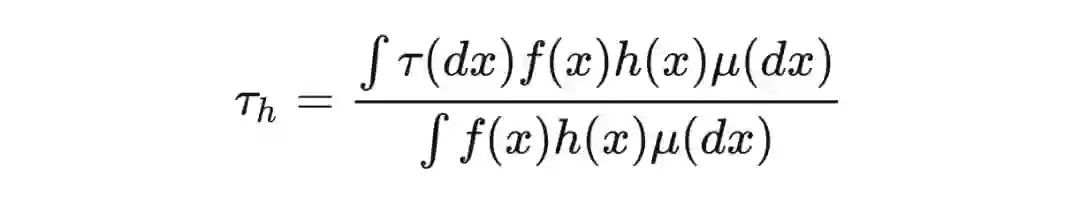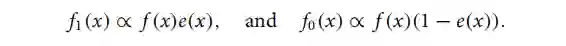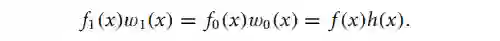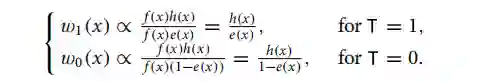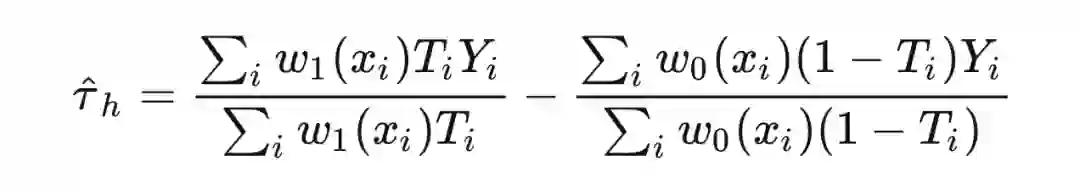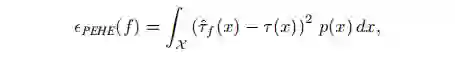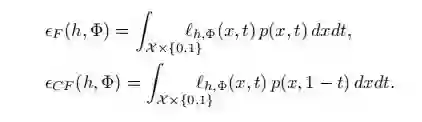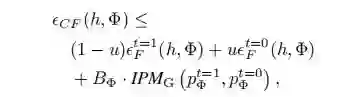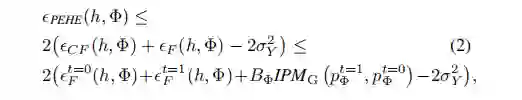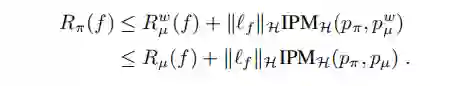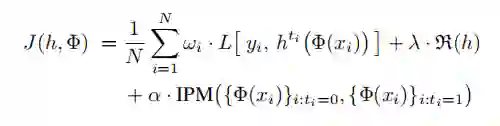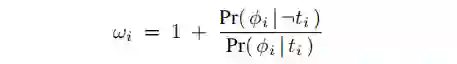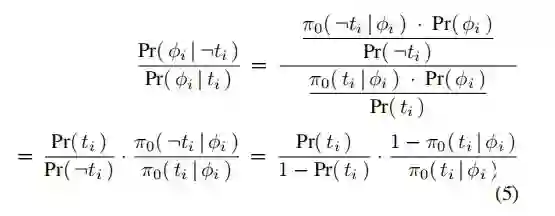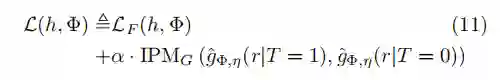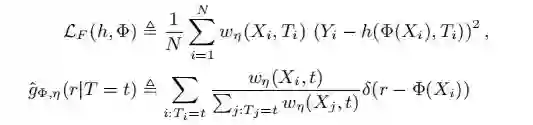因果效应估计组合拳：Reweighting和Representation

会员服务 ·

因果效应估计组合拳：Reweighting和Representation

2022 年 9 月 2 日 PaperWeekly

©作者 | Zicon

单位 | 广东工业大学

研究方向 | 因果推断

在潜在结果框架的语言下，基于观察数据，在 SUTVA，unconfounderness 与 overlap 假设成立的前提下，因果效应具有可识别性，即

。然而，为了无偏估计因果效应，我们还需要处理 confounder bias 的问题，即在观察数据中，confounder 会导致 treatment 组和 control 组的人群的协变量分布不同。

W‍eighting-based methods 和 Representation-based methods 是解决该问题的两种经典做法，这两种做法的原理是什么？又有什么改进空间？这就是这篇文章想稍微总结的东西。

Weighting-based methods

1.1 balancing weights

因果效应估计问题首先要定义感兴趣的目标人群（target population）以及目标估计量（estimand）：

举几个例子：如果我们将感兴趣的目标人群定义为整体人群，则我们的目标估计量为 ATE；如果我们将感兴趣的目标人群定义为 treatment 组的人群，则我们的目标估计量为 ATT；如果我们将感兴趣的目标人群定义为 control 组的人群，则我们的目标估计量为 ATC；如果我们将感兴趣的目标人群定义为treatment 组和 control 组分布平衡的协变量对应的人群，则我们的目标估计量为 ATO。

用形式化的语言来描述这一过程的话，假设总体人群的协变量的 marginal density 为，基本测度为，定义为预先定义的关于 x 的函数，用来过滤目标人群，因此我们可以将目标人群的 density 表示为，如此一来，定义在目标人群上的估计量可表示如下，其中。

定义好目标人群和估计量后。如前文所言，在一定假设下，我们可以证明目标估计量（因果效应）的可识别性，即因果效应是可以基于观察数据得到的。然而为了得到无偏的估计量，我们需要处理 treatment 组和 control 组协变量不平衡的问题。balancing weights 就是为了解决该协变量分布不平衡的问题提出来的，我们可以用下面的数学语言来描述其作用过程。

首先定义倾向性得分为，为 treatment 组人群的协变量 density，类似，表示 control 组人群的协变量 density，可以得到

balancing weights 的作用是：对每个个体赋予权重，使得 treatment 组和 control 组的协变量平衡，并对应目标人群。这句话用数学语言描述为：

具体的权重如何求？实际上，一旦我们确定了目标人群，即给定的情况下，balancing weights 也随之确定：

因此，基于观测数据样本，我们建立如下的无偏因果效应估计器：

也就是说，当我们确定目标人群的时候，目标估计量就确定了，描述目标人群的就确定了，balancing weights 也随之确定。

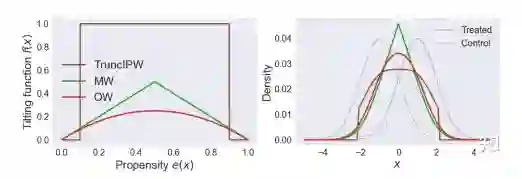
举个我们最熟悉的例子，假设我们确定目标人群为观察到的 treatment 组和 control 组的所有人群，则我们的目标估计量为 ATE，且，那么具体的 balancing weights 为，代入因果效应估计器得到。这其实就是我们最常用的 IPW —逆倾向性得分加权。

目标人群、、目标估计量和权重的对应关系见下表：

最后三个权重 OW，TruncIPW 和 MW，所选择的目标人群为协变量在 treatment 组和 control 组分布平衡的人群，如下图所示：

左图横坐标表示倾向性得分，纵坐标表示目标人群的过滤函数，这个图说明 OW 和 MW 倾向于给的人更大的权重，也就意味着该协变量在 treatment 组和 control 组分布平衡（TruncIPW 通过阈值 α 的选择，也能达到这个目的）；
右图浅色线分别表示 treatment 组与 control 组的 density，不同颜色的线分别对应不同的 balancing weights 加权后的人群分布，集中在 treatment 组和 control 组协变量分布较为平衡的区域。

1.2 covariate balance

1.1 节中提到的 balancing weights 是传统因果推断领域的经典方法，其主要是构建一个基于倾向性得分 e(x) 的函数来确定权重，从而实现协变量的平衡，但是该方法基于倾向性得分，因此难免不了倾向性得分本身存在的问题：模型错误指定、存在极端权重导致结果方差过大等。

近年来，也有人提出了另外一种学习权重的方法，将权重学习问题定义为在一定约束条件下，关于协变量分布的矩匹配（moment matching）/距离的优化问题，即通过拉齐 treatment 组和 control 组的分布，直接学习权重，从而避免需要倾向性得分所带来的问题，但这种做法难以拓展到高维上。

Representation-based methods

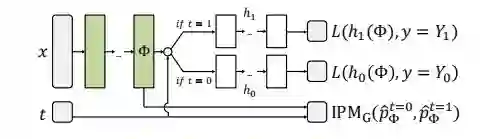
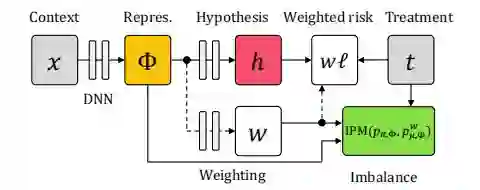
简单来说，Representation-based methods 的思路是从领域泛化的角度出发的：既然 confounders 影响了个体所接受的策略（X->T），进而导致 treatment 组和 control 组的协变量不平衡，那么干脆就学一个新的表征，该表征在 treatment 组和 control 组的分布平衡，且尽可能保留对Y的预测能力，同时丢掉与预测T有关的信息（把 X->T 这条边干掉，也就阻断了后门路径），从而避免了 confounders 带来的 bias。

这类方法的代表工作是 [2] 提出的 CFR/TARNet。其最终的损失函数是由关于 CATE 的 bound 导出的（因为我们的目标就是估计因果效应）。首先定义，那么估计的的期望损失为：

问题是，我们并不知道真正的，所以上式无法求解。经过推导可以发现，在一定假设下，可以被事实期望损失和反事实期望损失给 bound 住：

问题是我们拿不到反事实的数据，因此反事实期望损失也是无法求解的。但同样的，在一定假设下，可以被给 bound 住：

综上，在一定假设下，CATE 的期望损失的 upper bound 可表示为：

其中为 control 组样本关于 Y 的预测损失，为 treatment 组样本关于 Y 的预测损失，表示所学表征在 treatment 组和 control 组的分布距离。基于该 upper bound，可以得到最终的损失函数：

最小化上述损失函数意味着我们要：

最小化事实数据的预测损失（传统的监督学习任务），这本质上是要求学到的表征要尽可能保留关于 Y 的信息；
拉近和的分布距离，这本质上是要求学习的表征要尽可能丢掉关于 T 的信息。

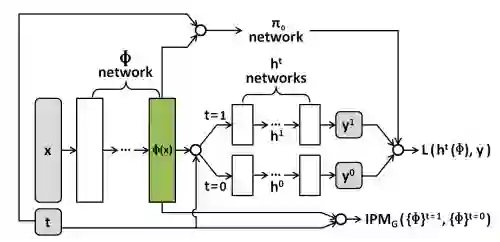
所以，这其实是一个关于 predictive accuracy 与 imbalance in the representation space 两者间的 trade-off。若太追求表征空间的平衡，可能会导致与Y有关的信息损失太多；若太追求预测准确性，可能会导致平衡不到位，confounder bias 仍然存在。基于该损失函数设计的网络结构如下图所示：

改进1：reweighting与representation的组合拳

既然 reweighting 与 representation 的方法都各自有优缺点，且刚好能够互补（比如 representation 方法会丢失信息，reweighting 方法则不会），那么能否把它们结合起来，更好地解决 confounder bias 的问题呢？这正是下面三篇文章的本质出发点，不过它们的 motivation 略有区别（讲了不同的故事）：

3.1 从bound出发

文章 [3] 与 [2] 是同一批作者，因此仍然从 upper bound 的角度进行推导。最终结论如下，在 representation 的基础上再进行 reweighting，能够获得一个比原来更加紧的 bound：

最终导出的 loss 为：

基于该损失函数设计的网络结构为：

3.2 从representation出发

文章 [4] 的出发点是：representation 方法本质上在做信息的取舍，为了保证消除 confounder bias，理论上应该追求完美的 balance，即把关于 T 的信息完全干掉，但这会导致部分对预测 Y 有用的信息也损失掉了，导致 predictive accuracy 下降。既然 reweighting 方法不会造成信息丢失，那可以采取的做法是：representation 承担大部分 balance 的任务，但不追求完美的 balance，剩下的部分由 reweighting 承担。

最终的损失函数为：

其中，权重的设计如下：

通过贝叶斯定义，上式第二项可化简为与倾向性得分有关的函数：

对应的网络结构如下所示：

3.3 从reweighting出发

文章 [5] 的出发点是：虽然理论上 balancing weights 可以实现完美的 covariate balance，但实际上我们往往学不到完美的权重，导致 confounder bias 没有完全去除。那么可以采取的做法是：reweighting 承担大部分 balancing 的任务，剩下的部分由 representation 承担。

最终的损失函数为：

其中：

这里的可以是 1.1 节中提到的任一 balancing weights（因此一开始需要先用逻辑回归拟合倾向性得分）。

3.4 小结

虽然上述三篇文章的出发点都是融合 reweighting 和 representation，但其 motivation 不同，模型的细节也稍有不同（从 motivation 出发，这些不同也很好理解）。下面从几个不同角度对做一些区分和总结：

从损失函数涉及到加权的位置看：3.1 和 3.3 在预测损失项和 IPM 项都分布涉及到了加权；3.2 只在预测损失项进行了加权；
从学习权重的输入空间看：3.1 和 3.2 的权重的输入空间是在表征空间上的，由于表征随着训练的 epoch 不断改变，因此和是需要反复交替训练的；3.3 的权重的输入空间是在协变量空间上的，因此在训练过程中，只要学习一次；
从学习表征的输入空间看： 3.1 和 3.2 表征映射函数的输入空间都是原始的协变量空间，即；3.3 表征映射函数的输入空间是加权后的协变量空间，即；
从学习权重的技术路线看：3.1 走的 1.2 中提到的，直接以缩小分布距离作为优化目标去学习权重的路线；3.2 和 3.3 走的是 1.1 节中提到的，balancing weights 的路线。

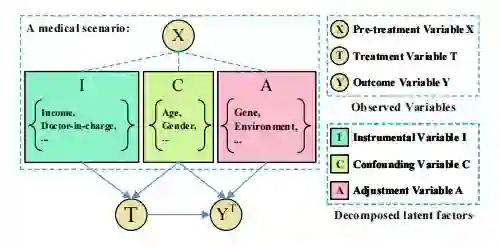
改进2：谁才是真正的confounders

针对于 reweighting 和 representation 的方法，还有另外一种可以改进的思路。我们可以发现，上面几节提出的方法都是直接把所有的协变量都当作 confounders，然而实际上可能并非如此，可能有些协变量只影响 T，我们称之为 Instrumental Variable；有些变量只影响 Y，我们称之为 Adjustment Variable；而同时影响 T 和 Y 的变量，才是 Confounder Variable。

也就是说，为了控制 confounder bias，我们其实只需要控制住真正的 confounder 变量，把非 confounder 变量考虑进来，不仅会造成要平衡的分布维度过高，还会产生额外的 bias。下面针对 reweighting 和 representation 两条技术路线，分别简单介绍两篇文章。

[6] 这篇文章，是在 reweighting 框架下更加细粒度地控制 confounder bias 的，具体走的 1.2 节中提到的，通过拉齐协变量分布的一阶矩来学习样本权重。此外，还 额外引入了 confounder weights 来判断每个协变量是否是 confounders 以及其对 confounder bias 的贡献。

具体而言，文章的目标估计量是 ATT，对数据生成过程做了如下的线性假设：

，通过推导发现在上述假设下，具潜在结果对协变量X回归得到的参数，正好就是要求的 confounder weights：

[7] 这篇文章，是在 representation 框架下更加细粒度地控制 confounder bias 的。其对数据生成过程的假设如下面因果图所示：

因此，借助图上的一些条件独立性性质，例如，，我们可以首 先将协变量 解耦成 三部分 ，再将的分布调整到 balance，最后基于去预测 Y 即可。

参考文献

[1] Li F, Morgan K L, Zaslavsky A M. Balancing covariates via propensity score weighting[J]. Journal of the American Statistical Association, 2018, 113(521): 390-400.

[2] Shalit U, Johansson F D, Sontag D. Estimating individual treatment effect: generalization bounds and algorithms[C]//International Conference on Machine Learning. PMLR, 2017: 3076-3085.

[3] Johansson F D, Kallus N, Shalit U, et al. Learning weighted representations for generalization across designs[J]. arXiv preprint arXiv:1802.08598, 2018.

[4] Negar Hassanpour and Russell Greiner. Counterfactual regression with importance sampling weights. In Proceedings of the Twenty-Eighth International Joint Conference on Artifificial Intelligence, IJCAI-19, pp. 5880–5887, 2019.

[5] Assaad S, Zeng S, Tao C, et al. Counterfactual representation learning with balancing weights[C]//International Conference on Artificial Intelligence and Statistics. PMLR, 2021: 1972-1980.

[6] Kuang K, Cui P, Li B, et al. Estimating treatment effect in the wild via differentiated confounder balancing[C]//Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining. 2017: 265-274.

[7] Wu A, Kuang K, Yuan J, et al. Learning decomposed representation for counterfactual inference[J]. arXiv preprint arXiv:2006.07040, 2020.

更多阅读