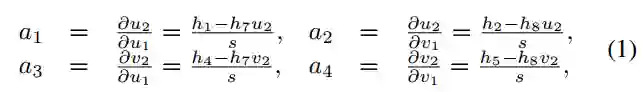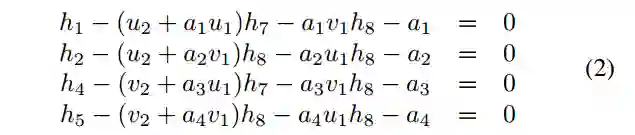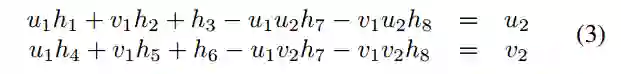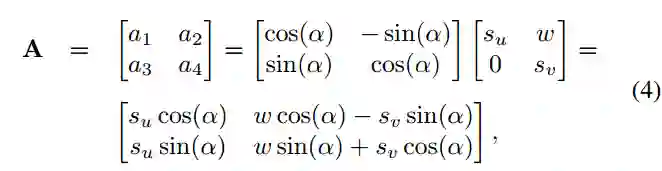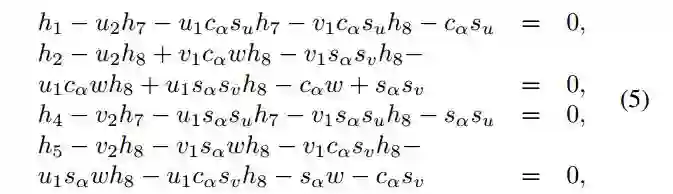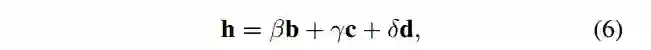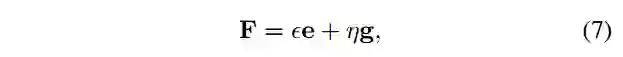【泡泡图灵智库】无标定相机的五点法基本矩阵估计（CVPR）

泡泡图灵智库，带你精读机器人顶级会议文章

标题：Five-point Fundamental Matrix Estimation for Uncalibrated Cameras

作者：Daniel Barath

来源：CVPR 2018

编译：谢泽茹

审核：侯延华

欢迎个人转发朋友圈；其他机构或自媒体如需转载，后台留言申请授权

摘要

       大家好，今天为大家带来的文章是——无标定相机的五点法基本矩阵估计，该文章发表于CVPR 2018。

       

        本文提出一种算法，使用两视图中的五对旋转不变特征（如SIFT特征点）就能估计出基本矩阵。首先，使用共面的三个点并结合它们的旋转分量估计得到单应矩阵，然后再引入额外的两个点来计算出基本矩阵。作者提出的方法能够与像基于图割优化的RANSAC算法等鲁棒估计方法相结合，通过合成图像和561对真实图像上的实验验证了该方法在准确性和所需迭代次数方面上均优于其他最先进的算法。此外，城市环境中算法实测过程中发现对三点共面的要求并不十分苛刻：即使这些点不是完全共面的，局部优化的鲁棒估计也能推得准确的估计。此外，本文所提出的方法能应用在双视图多运动的估计上，使结果更准确。

主要贡献

        1、我们提出了一种使用三对旋转不变特征来估计单应性矩阵H的方法。为了恢复单应性矩阵H，除了点坐标之外，还加入了特征描述的旋转部分。

        2、使用附加的两个点对可使恢复的单应性矩阵H用于计算基本矩阵F。

        3、在合成数据和现实世界的测试中，本文所提出的方法与鲁棒估计（如局部最优的RANSAC算法）结合后，在精度和所需迭代次数方面均优于现有技术。并证明在双视图多运动拟合中使用本文所提出的方法能得到更准确的聚类。

算法流程

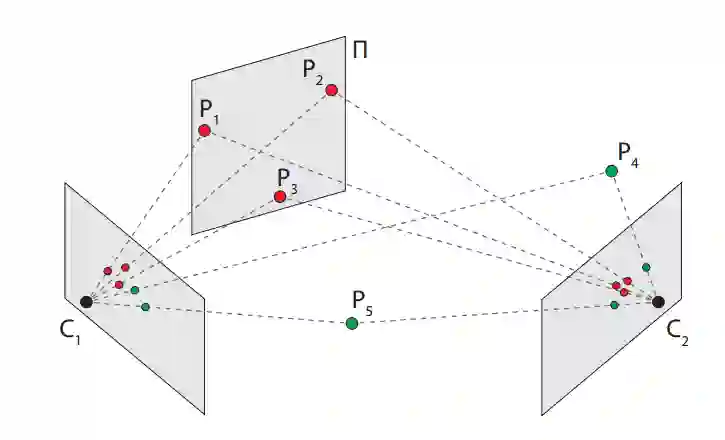
图1 提出最小解求解方法估计在两个视图C1和C2之间的基本矩阵

       本文先估计平面Π上三个点（P1，P2和P3）对应位置的单应性矩阵，然后从单应性矩阵和两个附加的点（P4和P5）的位置获得基本矩阵。

        先将仿射变换关系（AC）设为三元组：（p1，p2，A），其中p1 = [u1 v1 1] T和p2 = [u2 v2 1] T是两个图像（图1中3D点的投影）中对应的齐次点对，A为2×2的局部仿射变换，在透视摄像机中是相应的3×3单应性矩阵H的一阶近似。

如下所述：

其中，ui和vi是第i个图像中的坐标（i∈{1,2}），hj是行优先的H矩阵中的第j个元素（j∈[1,9]），s = u1h7 + v1h8 + h9 是射影深度。

1 单应性和仿射变换关系

        一个仿射变换可以得到6个线性方程：

前4个等式显示了局部仿射变换和单应性的联系，后两个等式显示了单应性和一个点对应关系Hp1∼p2。

        将仿射变换模型定义为线性变换的组合，如下所示：

其中α,s_u,s_v和w分别表示旋转角,沿着轴u和轴v的缩放比例和剪切参数。

        将式子4带入到式子2中，替换矩阵中定义的分量，给出如下系统：

其中，c_α=cos⁡(α)，s_α=sin⁡(α)。该系统表示了影响相关单应性的仿射参数的一般方式。

2 单应性矩阵估计

        通过所有对应关系得到Hp1,i~p2,i（式子3）作为齐次线性系统Bh = 0。由于每个点对各自产生九个未知数的两个方程，因此系数矩阵B的大小为6×9，且h = [h1 h2 h3 h4 h5 h6 h7 h8 h9] T是未知参数的矩阵表示。B的零空间是三维的，因此最终结果为三个零向量的线性表达，如下所示：

其中b = [b1 ... b9] T，c = [c1 ... c9] T和d = [d1 ... d9] T是零矢量，β，γ，δ是未知标量。 由于H的非单值性，其中一个可以设置为任意值，因此在我们的算法中设定δ= 1。

        给出的三个旋转分量通过式子（5）各能列出四个方程和三个未知数。两个旋转角能产生八个方程和六个未知数，估计出β和γ的值。最后，通过式子（6）可重新算得单应性矩阵H。

4 五个对应点的基本矩阵估计

    使用估计的H和两个附加对应关系通过p_(2,i)^T Fp_(1,i)=0（i∈[1,7]）产生七个线性方程，得出以下齐次线性系统：Df = 0，其中f = [f1 f2 f3 f4 f5 f6 f7 f8 f9] T是未知参数的向量；D是系数矩阵，为

矩阵D的零空间是二维的，结果为两个零向量的线性表示：

其中ϵ和η是未知标量，e = [e1 ... e9] T和g = [g1 ... g9] T是零向量。

        由于F的非单值性，η可以设置为任意值。为了实现稳定性，我们设定η= 1 - ϵ，从而将权重之和保持为1。把式子（7）代入det（F）= 0，得到一个三次多项式方程。获得ϵ（它们的值为{1,2,3}，类似于七点算法）的可能解作为多项式的实根。最终把ϵ代入式子（7）得到基本矩阵F。

主要结果

1  合成数据测试

        通过投影矩阵P1，P2∈R（3×4）生成两个透视摄像机，并且对五个随机平面进行采样，每个平面可以分别放在四个位置上。 然后将生成的20个点投射到摄像机中，并根据图像点和平面参数计算地面真实的仿射变换。零均值的高斯噪声被添加到点坐标，因此也干扰了仿射分量。

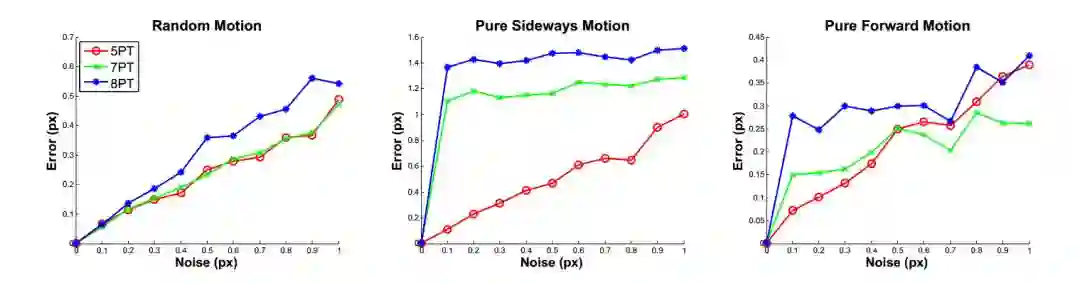
图2 本文所提出的算法和七点算法、八点算法在摄像机运动中的平均误差

所提出的方法与一般运动的七点算法具有相似的精度。然而对于侧向运动，该方法对噪声的敏感性明显低于算法。对于前向运动，如果噪声σ不超过0.5，则五点算法最准确；σ超过0.5后，七点算法较优。

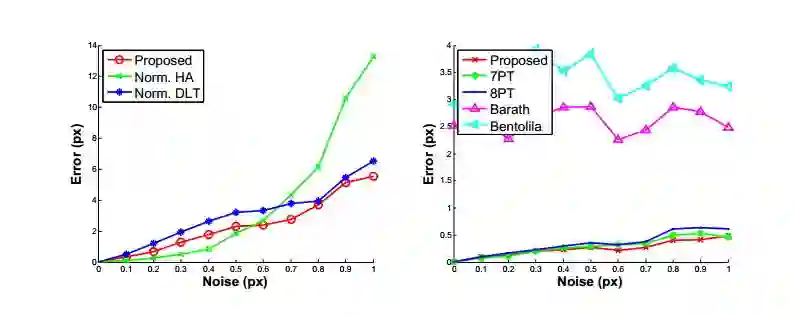
图3

（左）单应性估计与标准化HA 和DLT方法的比较结果

（右）5PT方法与（7PT，8PT）和Barath等人提出方法的比较结果

对比本文所提出的算法和7PT算法、8PT算法，可以观察到与先前测试集相同的趋势。还可以看出，基于AC的方法中，A的近似太差。

2 真实数据测试

        本文使用了AdelaideRMF2，Kusvod23，Multi-H4和Strecha5数据集（参见图5的示例）来进行测试。 

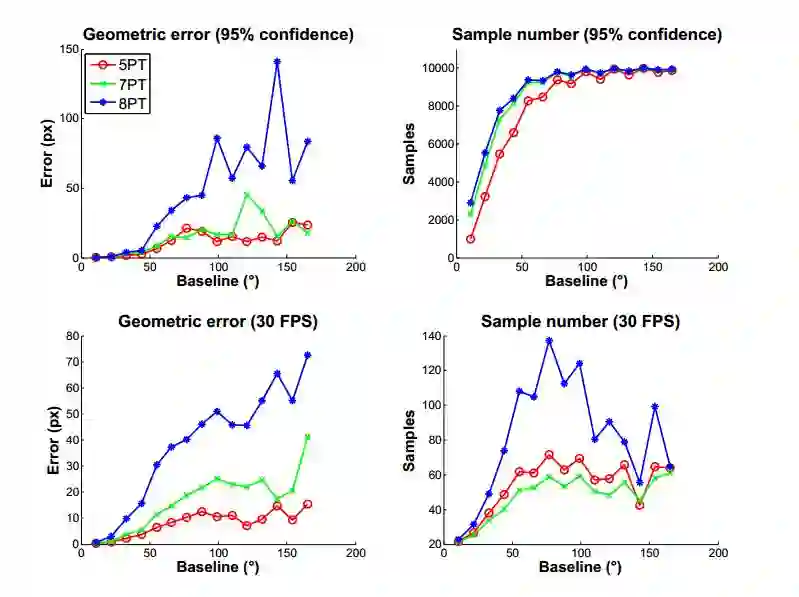
图4 在Strecha数据集的每个图像对（＃515）上的100次运行计算结果

图5 该方法与基于图像分割的RANSAC算法相结合的结果。

可以看出，结果很好：极线通过第一（左）和第二（右）图像中的相同像素。（a）和（b）显示出有趣的效果：没有完全共面的三点。 然而，最初估计的基本矩阵足够精确，可以通过GC-RANSAC的局部优化步骤进行精确细化。

3 应用：刚体运动分割

        在AdelaideRMF运动数据集上进行了评估（参见图6），包括18个图像对和地面实况——分配给它们运动的聚类或异常类的对应关系。

图6 示例结果

（在AdelaideRMF运动数据集上应用PEARL和本文提出的方法）

颜色表示运动，黑点表示异常值。

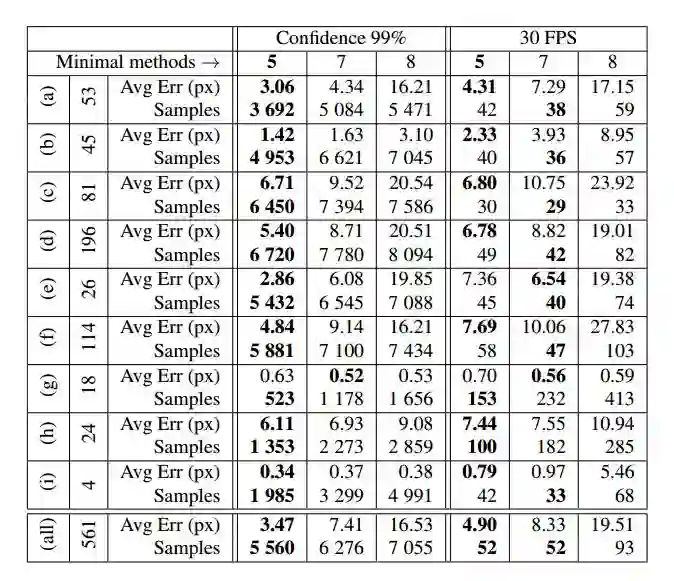
表3 基本矩阵估计（在Strecha数据集上使用GC-RANSAC和最小方法）

        PEARL对所有方法使用相同的初始模型编号，针对每个问题和每个方法分别调整了inlier-outlier阈值。 可以看出，五点算法获得的聚类是最准确的。

4 运行时间

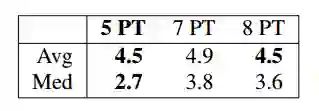
表4 PEARL的平均值和中值误分类误差

        本文提出方法使用OpenCV进行100次C ++实现的平均处理时间为0.16毫秒。结合诸如RANSAC的假设和验证的鲁棒估计后能减少运行时间，因为它们的处理时间的数量级取决于所需的最小样本的大小。

Abstract

        We aim at estimating the fundamental matrix in two views from five correspondences of rotation invariant features obtained by e.g. the SIFT detector. The proposed minimal solver first estimates a homography from three correspondences assuming that they are co-planar and exploiting their rotational components. Then the fundamental matrix is obtained from the homography and two additional point pairs in general position. The proposed approach, combined with robust estimators like Graph-Cut RANSAC, is superior to other state-of-the-art algorithms both in terms of accuracy and number of iterations required. This is validated on synthesized data and 561 real image pairs. Moreover, the tests show that requiring three points on a plane is not too restrictive in urban environment and locally optimized robust estimators lead to accurate estimates even if the points are not entirely co-planar. As a potential application, we show that using the proposed method makes two-view multi-motion estimation more accurate.

如果你对本文感兴趣，想要下载完整文章进行阅读，可以关注【泡泡机器人SLAM】公众号。

点击阅读原文，即可获取本文下载链接。

欢迎来到泡泡论坛，这里有大牛为你解答关于SLAM的任何疑惑。

有想问的问题，或者想刷帖回答问题，泡泡论坛欢迎你！

泡泡网站：www.paopaorobot.org

泡泡论坛：http://paopaorobot.org/bbs/

泡泡机器人SLAM的原创内容均由泡泡机器人的成员花费大量心血制作而成，希望大家珍惜我们的劳动成果，转载请务必注明出自【泡泡机器人SLAM】微信公众号，否则侵权必究！同时，我们也欢迎各位转载到自己的朋友圈，让更多的人能进入到SLAM这个领域中，让我们共同为推进中国的SLAM事业而努力！

商业合作及转载请联系liufuqiang_robot@hotmail.com