【电子书】《计算机视觉中的多视图几何(第2版)》英文版，Multiple View Geometry in Computer Vision，附673页PDF

书名： Multiple View Geometry in Computer Vision

主要内容：

该书分为六个部分，并有七个简短的附录。每个部分都引入了一个新的几何关系:背景的单应性，单视点的相机矩阵，两视点的基本矩阵，三视点的三焦张量，四视点的四焦张量。在每种情况下，都有一章描述这种关系、它的性质和应用，并有相应的一章描述从图像测量中进行估计的算法。所述的估计算法范围从廉价、简单的方法到目前被认为是最佳可用的最优算法。

第0部分:背景 这一部分比其他部分更像是教程。介绍了2-空间和3-空间射影几何的中心思想(如理想点和绝对二次曲线);几何图形如何表示、处理和估计;以及几何图形如何与计算机视觉中的各种目标相联系，如校正平面图像以消除透视畸变。

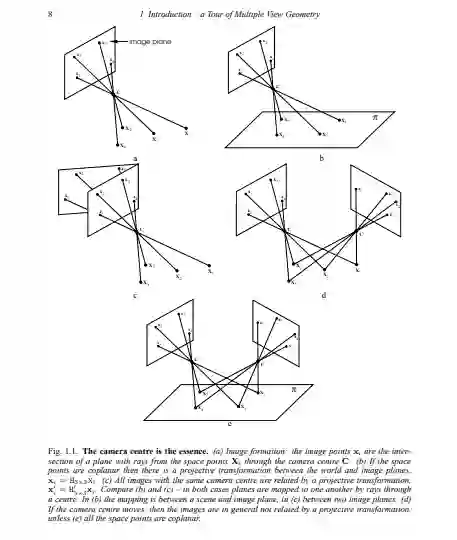
第1部分:单视图几何 在这里，各种各样的相机模型的透视投影从3-空间到一个图像的定义和他们的解剖探索。介绍了利用传统的标定对象技术进行标定的方法，以及从消失点和消失线进行摄像机标定的方法。

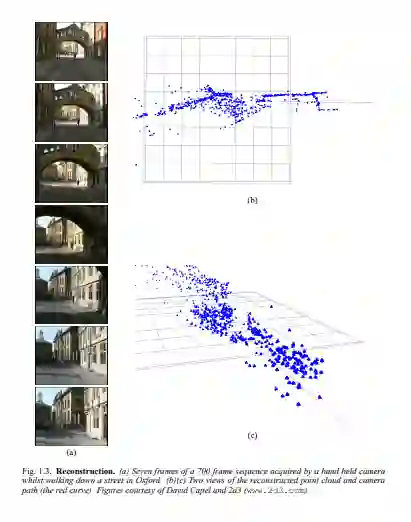
第2部分:双视图几何 介绍了双摄像机的极外几何结构、图像点对应的射影重建、射影模糊的解决方法、最佳三角剖分、通过平面实现视图之间的转换。

第3部分:三视图几何 这里描述了三个相机的三焦几何结构，包括点对应从两个视图到第三个视图的转换，以及线对应的类似转换;计算几何从点和线对应，检索相机矩阵。

第4部分:多视角 这部分有两个目的。首先，它将三视图几何扩展到四个视图(一个较小的扩展)，并描述了适用于n视图的估计方法，例如Tomasi和Kanade的因式分解算法，用于同时从多个图像计算结构和运动。其次，它涵盖了在前几章中提到过的主题，但通过强调它们的共性，可以更全面、更一致地理解这些主题。示例包括推导对应关系的多线性视图约束、自动校准和模糊解决方案。

附录： 这些描述了进一步的背景资料张量，统计，参数估计，线性和矩阵代数，迭代估计，稀疏矩阵系统的解，和特殊的投影变换。