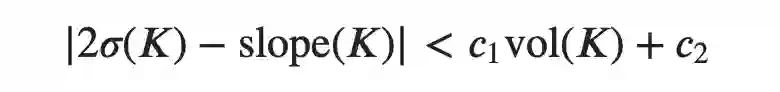DeepMind让AI变身天才数学家！首次提出两大数学猜想，登Nature封面

---

  新智元报道  

编辑：编辑部

【新智元导读】12月2日，DeepMind用AI帮助数学家们提出了两个全新的数学猜想，再次登上Nature封面！

AI发现两大数学猜想登上Nature封面，背后的功臣又是DeepMind！

 

这次，机器学习首次发现了被人类忽略的数学联系。

 

数学的实践，简单来说就是发现某种模式，并利用这些模式来提出和证明猜想，从而形成定理。

 

近日，DeepMind利用机器学习在扭结理论（Knot theory）和表示论（Representation theory）两个领域协助数学家们发现了全新的猜想和定理。

 

 

自20世纪60年代以来，数学家们就在利用计算机来协助发现模式和提出猜想，其中最有名的是千禧年大奖难题之一——Birch and Swinnerton-Dyer conjecture（贝赫和斯维讷通-戴尔猜想）。

 

 

为了发现数学对象之间的潜在模式和关联，DeepMind研究团队提出采用一种全新机器学习模型，用归因技术加以辅助理解，并利用这些观察进一步指导直觉思维和提出猜想的过程。

 

论文「Advancing mathematics by guiding human intuition with AI」已于12月1日在Nature发表。

 

扭结理论

 

低维拓扑学是一个活跃而有影响力的数学领域。

 

 

扭结，是三维空间中的简单封闭曲线，也是低维拓扑中的基本对象之一。

 

在数学语言中，结是一个圆在3维欧几里得空间中的嵌入。如果两个数学结可以通过R的变形转化为另一个结，那么这两个结就是等价的。

 

研究人员发现，在这个问题上，可以利用计算机视觉（CV）领域常用的「显著图」（Saliency map）技术。在CV任务中，该技术可以确定图像的哪些部分携带相关度最高的信息。

 

通过这一技术，计算机给出了多个结中可能存在关联的属性，还生成了一个似乎适用于所有情况的公式。

 

 

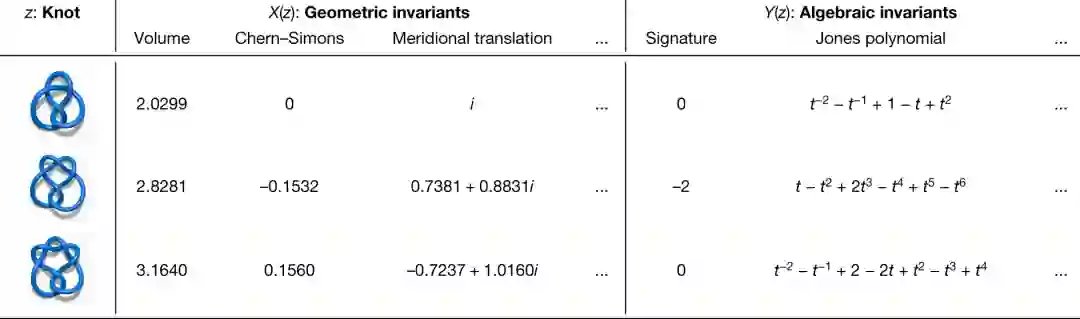
对于扭结的研究，其中一个方法是通过不变量来实现的，不变量是对任何两个等价结都相同的代数、几何或数字量。

 

这些不变量有许多不同的推导方式，论文主要关注其中两个主要类别：双曲不变量和代数不变量。这两类不变式是由相当不同的数学学科推导出来的，因此，在它们之间建立联系是相当有意义的。

 

一个值得注意的猜想联系的例子是体积猜想，它提出一个结的双曲体积（hyperbolic volume，几何不变量）应该被编码在其彩色琼斯多项式（coloured Jones polynomials ，代数不变量）的渐近行为中。

 

不变量的例子

 

研究人员的假设是，在一个纽结的双曲不变量和代数不变量之间存在着一种未被发现的关系。

 

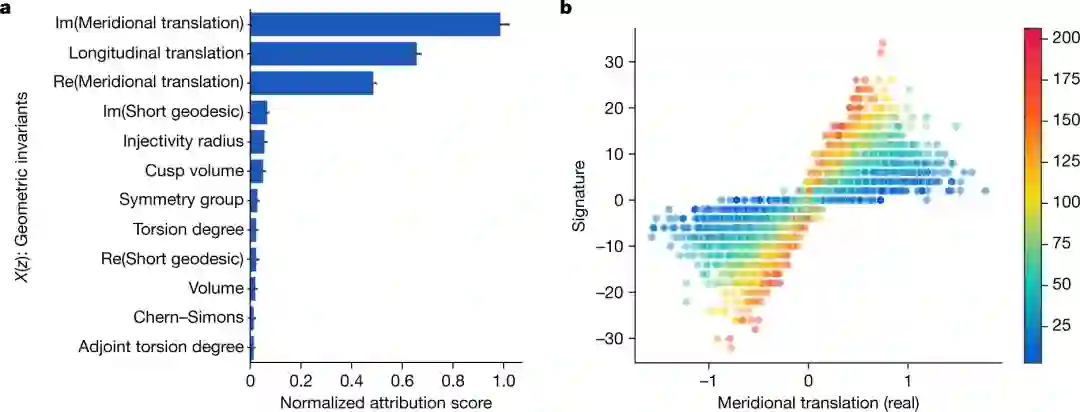
于是，DeepMind通过一个监督学习模型发现了结的几何不变量和一个特定的代数量signature σ(K)之间存在直接联系，而这在以前是完全未知的，现有的理论也无法给出任何提示。

 

用归因技术确定三个不变量最相关的特征，并被部分可视化

 

此外，通过使用机器学习的归因技术，DeepMind引入了一个新的数量「自然斜率」，其定义为slope(K) = Re(λ/μ)，其中Re表示实部。

 

猜想：存在常数c1和c2，使得对于每个双曲结K。

 

 

这个猜想得到了几个从不同分布中取样的大型数据集的分析支持。

 

定理：存在一个常数c，使得对于任何双曲结K。

 

 

事实证明，即使对于规模非常大的一类纽结，这个公式都是适用的。

 

在生成的整个数据集中，可以把c≥0.23392作为下限，有理由猜测c最多为0.3，这在计算的区域内给出了一个紧密的关系。

 

令人惊讶的是，在一个已经被广泛研究的领域中，像这样一个简单而深刻的联系竟然被忽略了。

 

内布拉斯加大学林肯分校的纽结理论家Mark Brittenham说：「这篇文章以非常直接的方式证明了这些不变量的相关性，这表明，我们在这个领域还有一些基本的东西没有完全理解。」

 

表示论

 

表示论将抽象代数结构中的元素「表示」成向量空间上的线性变换，并研究这些代数结构上的模，从而研究结构的性质。同时，表示论也是关于线性对称的理论。

 

围绕有限的对象集进行转换的「对称性」问题，在数学的几个分支中都具有重要意义，长期以来都是数学家的研究热点，使用的工具包括图和多项式等。

 

 

悉尼大学的Geordie Williamson教授表示，过去几十年来，研究人员一直希望可能从网络中计算出多项式，但这个目标似乎一直遥遥无期。

 

图会变得过于庞大和复杂，「很快就超出了人类的理解范围」。

 

现在，有了计算机的帮助，他和团队注意到，是不是可以将图分解成更小、更容易管理的多个部分，各部分都具有高维立方体结构。

 

Williamson表示，AI的强大让他深感震撼。一旦机器学习算法锁定了某个模式，就能非常精确地猜测哪些图和多项式来自相同的对称性，而且竟然猜得如此之准！

 

 

近40年来，组合不变性猜想一直未能取得进展，该猜想指出对称群SN中两个元素的KL多项式可以从它们的无标记的Bruhat区间，即一个有向图中计算出来。

 

不可约表示受Kazhdan-Lusztig（KL）多项式的影响，它与组合学、代数几何和奇点理论有着深刻的联系。

 

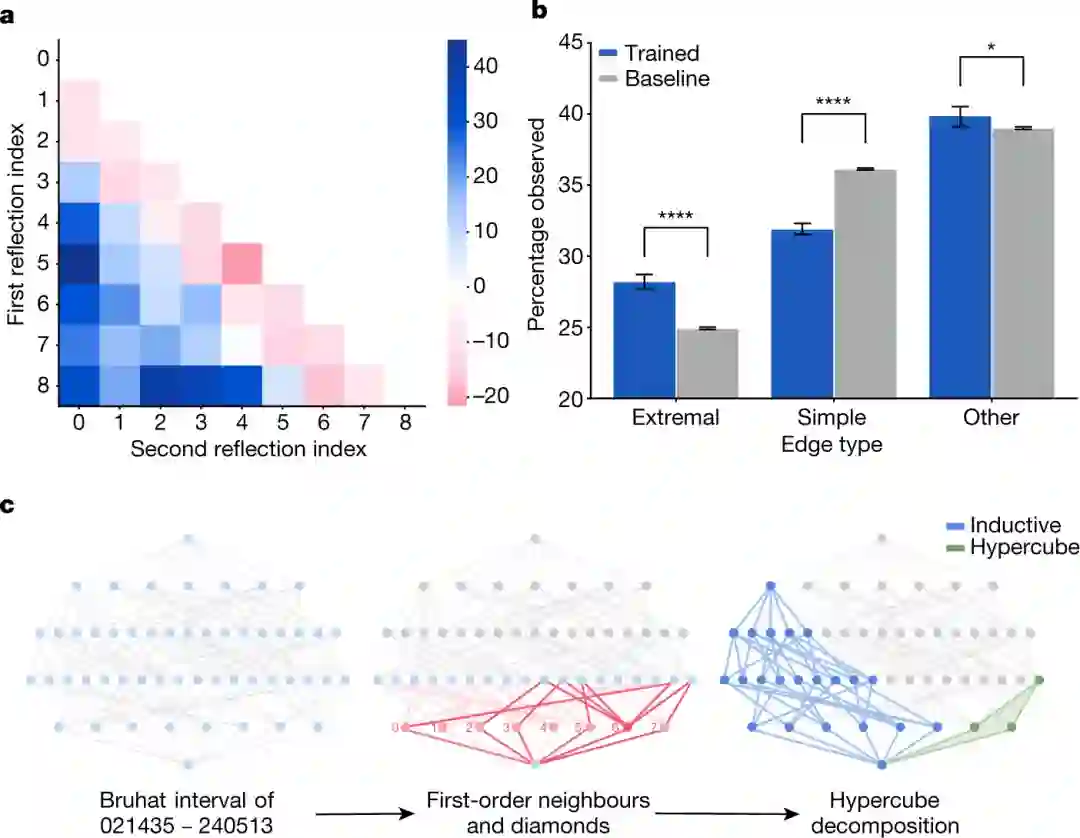
其中，Bruhat区间是一个图表，它代表了通过一次只交换两个对象来反转对象集合顺序的所有不同方式。而KL多项式告诉了数学家一些关于这个图在高维空间中存在的不同方式。有趣的结构只有在Bruhat间隔有100或1000个顶点时才开始出现。

 

在理解这些对象之间的关系方面取得进展的一个障碍是，非三阶KL多项式（不等于1的那些）的Bruhat区间是非常大的图，很难形成直观的认识。

 

 

将这个猜想作为初始假设，DeepMind发现了一个能够以相当高的精度预测Bruhat区间的KL多项式的监督学习模型。

 

通过改变向神经网络输入Bruhat区间的方式，DeepMind发现一些图形和特征的选择特别有利于预测的准确性。特别是当有了更准确的估计函数的支持，通过一些子图就足以计算出KL多项式。

 

通过计算归因技术可以确定最相关的子图，并分析这些图与原始图的边缘分布，发现了进一步的结构证据。

 

在下图a中，DeepMind通过「反射」来汇总的子图中边缘的相对频率。

 

结果表明，极值反射（形式为[0，i]或[i，N-1]的SN）更多地出现在最相关的子图中，而简单的反射（形式为[i，i+1]）则被放弃掉了，这一点经过多次模型的再训练也得到了证实。

 

从KL多项式的定义来看，简单反射和极值反射之间的区别与子图相关性的联系是很直观的。考虑到这一现象，DeepMind发现一个Bruhat区间可以一个自然地分解为两个部分：由一组极值边诱导的超立方体和一个与SN-1中的区间同构的图。

 

 

定理：每个Bruhat区间都有一个沿其极值反射的典型超立方体分解，从中可以直接计算出KL多项式。

 

值得注意的是，进一步的测试表明，所有超立方体分解都能确定KL多项式。这一点在S7以下的对称群中的所有3×106个区间以及S8和S9的非同构区间中的1.3×105个区间都得到了计算验证。

 

猜想：无标签的Bruhat区间的KL多项式可以用前面的公式计算出任何超立方体分解。

 

如果这个猜想能够被证明，那么对称群的组合不变性猜想就可以得到解决。

 

发现数学猜想，AI化身天才数学家

 

一个多世纪以前，Srinivasa Ramanujan以其在数字中看到其他人看不到的非凡模式的能力震惊了数学界。这位来自印度的自学成才的数学家，将他的洞察力描述为「深刻的直觉和精神」。

 

众所周知，数学家的直觉在数学发现中起着极其重要的作用——只有将严谨的形式主义和良好的直觉思维相结合，才能解决复杂的数学问题。

 

几个世纪前，人们就发现了凸多面体性质之间的关系：无论形状如何，顶点的数目 (v) 减去边的数目 (e) 加上面的数目 (f) 等于2，即 v-e+f=2。

 

描述这种关系的公式叫「欧拉公式」，是以瑞士数学家Leonhard Euler的名字命名，被人们称为上帝公式。

 

 

数学家一般是通过循环往复的研究学习例子来发展数学理论。此外，还需要需要创造力和计算能力。

 

在这种简单问题情况下，他们可以用纸和笔研究几个不同形状的例子得出这个公式。

 

但是，当遇到更复杂的数学问题时就会需要更广泛的计算，就不得不需要机器学习来助力。

 

从20世纪60年代开始，数学家开始使用计算机帮助发现规律和提出猜想，但一直以来AI系统尚未普遍应用于理论数学研究领域。

 

DeepMind在论文中描述的这通用的机器学习框架方法，让数学家们可以使用ML工具来指导他们对复杂数学对象的直觉，验证关系存在的假设，并理解这些关系。

 

 

通过训练机器学习模型来估计特定数据 PZ 分布上的函数，该过程有助于引导数学家对假设函数 f 的直觉思维。

 

对学习函数 fˆ 的准确性和应用于它的归因技术的见解可以帮助理解问题和构建封闭形式的 f'。

 

同时，这一过程是迭代和交互的，而不是一系列的步骤。

 

研究结果证明，在数学家的直觉思维指导下，机器学习提供了一个强大的框架，可以在有大量数据可用的领域，或者对象太大而无法应用经典方法研究的领域，发现有趣且可证明的猜想。

 

正如研究者总结道，「直觉在许多人类追求的超常表现中扮演着重要的角色。」

 

比如，它对顶级围棋玩家至关重要，AlphaGo之所以能够成功，部分原因就是它通过机器学习来学习人类凭直觉判断游戏元素的能力。

 

 

数学确实是一项与围棋截然不同、更具合作性的工作，因此AI在协助数学家完成相关方面的工作，的确具备卓有成效的空间和潜力。

 

参与这项研究的数学家之一、英国牛津大学的Marc Lackenby说：「我非常震惊于机器学习工具是多么有用。我没有想到我的一些先入为主的观念会被颠覆。」

 

数学家Jeffrey Weeks说，他自20世纪80年代以来一直开创了其中的一些技术。但是利用AI，让计算机寻找模式，让这一研究有了质的提升。

参考资料：

https://www.nature.com/articles/s41586-021-04086-x https://www.nature.com/articles/d41586-021-03593-1 https://deepmind.com/blog/article/exploring-the-beauty-of-pure-mathematics-in-novel-ways