DeepMind Nature发文：AI能提出和证明数学定理

2021 年 12 月 2 日 学术头条

作为一门古老的学科，数学的内容包括发现某种模式，并使用这些模式来表述和证明猜想，从而产生定理。

自 20 世纪 60 年代以来，数学家们一直使用计算机来帮助发现猜想的模式和公式，最著名的案例是 Birch and Swinnerton-Dyer conjecture（贝赫和斯维讷通-戴尔猜想），这个猜想是千禧年数学大奖的七个问题之一，是数论领域的著名问题。

但是，时至今日，计算机证明基础数学重要定理的例子也并不多见。

现在，DeepMind 的一项成果展示了更多的可能性：计算机科学家和数学家们首次使用 AI 来帮助证明或提出新的数学定理，包括复杂理论中的纽结理论（knot theory）和表象理论（representation theory）。

这些让人惊喜的结果，今天发表在著名的科学杂志Nature上，其论文标题为“Advancing mathematics by guiding human intuition with AI”（人类直觉与 AI 推动数学的前进）。

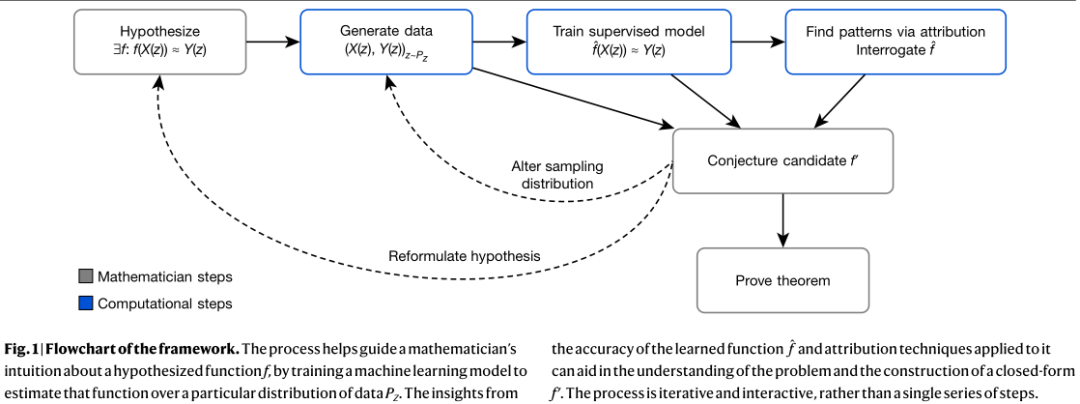
在该论文中，作者团队提出采用一种机器学习模型，来发现数学对象之间的潜在模式和关联，用归因技术加以辅助理解，并利用这些观察进一步指导直觉思维和提出猜想的过程。

乔迪·威廉姆森教授（Geordie Williamson）是悉尼大学数学研究所所长，也是世界上最重要的数学家之一，他在纯数学领域有着非凡的成绩。作为该论文的合著者，他成功发挥 Deep Mind 的 AI 力量，在其的专业领域——表象理论中展开了大胆的探索猜想。

图丨Geordie Williamso

而熟悉人工智能的读者对 DeepMind 并不陌生。这个 AlphaGo 背后的计算机科学家团队，曾在 2016 年围棋比赛中，让 AI 成功击败世界冠军。在那之后，DeepMind 一直秉承的理念是，要用 AI 助力解决重大科学问题。

基础数学无疑属于重大科学问题的范畴（甚至可以说是地基）。正如 Geordie Williamson 教授所说：“数学问题一度被认为是最具智力挑战性的问题……虽然数学家们已经使用 ML 来帮助分析复杂的数据集，但这是我们第一次使用计算机来辅助形成猜想，或为数学中未经证实的想法提出可能的突破路线。”

助力顶尖数学家证明数学猜想

这次研究中，AI 帮助探索的数学方向是表象理论。表象理论属于线性对称理论，是利用线性代数探索高维空间的数学分支，而 Williamson 教授是全球公认的表象理论的领导者。在 2018 年，他成为伦敦皇家学会（Royal Society）最年轻的在世会员，该学会则是世界上最古老、可以说是最负盛名的科学协会。

Williamson 教授说：“在我所研究的领域中，为了证明或反驳长期存在的猜想，有时需要考虑跨越多维度的无限空间和极其复杂的方程组”。虽然计算机长期以来一直被用来为实验数学生成数据，但识别有趣模式的任务主要依赖于数学家自己的直觉。

众所周知，数学家的直觉在数学发现中起着极其重要的作用——“只有结合严格的形式主义和良好的直觉思维，才能解决复杂的数学问题”。

然而，现在的情况有所改变。

如上图所示，论文中描述了一种通用的框架方法，在这个框架方法之下，数学家可以使用 ML 工具来指导他们对复杂数学对象的直觉，验证关系存在的假设，并理解这些关系。

Williamson 教授就利用 DeepMind 的 AI，在证明关于 Kazhdan-Lusztig 多项式的古老猜想的道路上离目标越来越近，当然，这些猜想涉及高维代数中的深度对称性。可以说，Kazhdan-Lusztig（KL）是代数群表示论近 40 年来最重要的发展之一。

而来自牛津大学（University of Oxford）的 Marc Lackeby 教授和 András Juhász 教授，则进一步研究了这一过程。

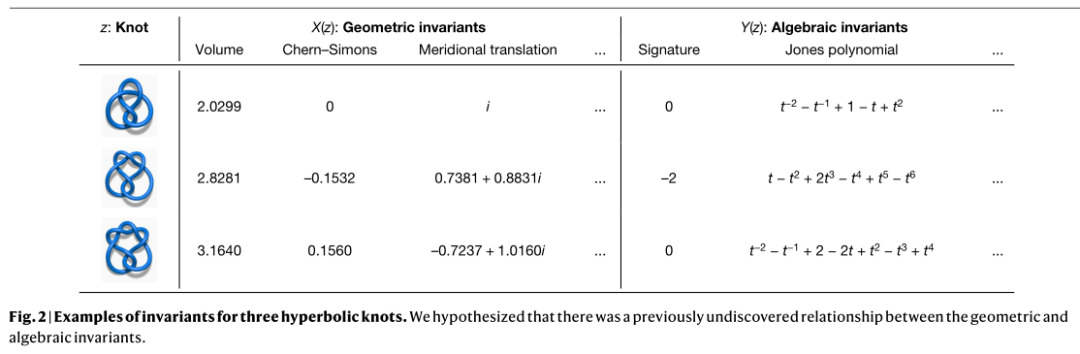
他们发现了纽结的代数和几何不变量之间惊人的关联，建立了数学中一个全新的定理。这些不变量有许多不同的推导方式，研究团队将目标主要聚焦在两大类：双曲不变量和代数不变量。两者来自完全不同的学科，增加了研究的挑战性和趣味性。图 2 给出了不变量的一些示例。

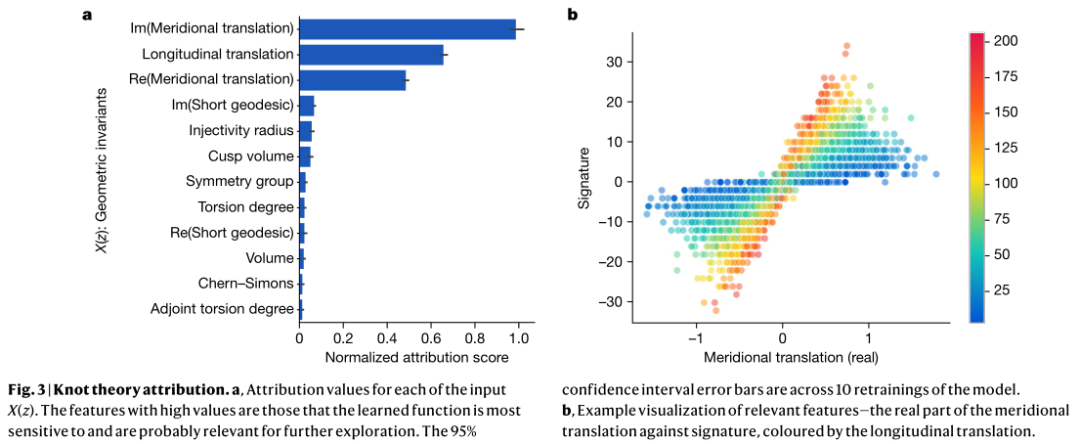
研究团队假设，在一个纽结的双曲不变量和代数不变量之间存在着一种未被发现的关系。监督学习模型能够检测到大量几何不变量和签名之间存在的模式。如下图所示，由归因技术确定最相关的特征。

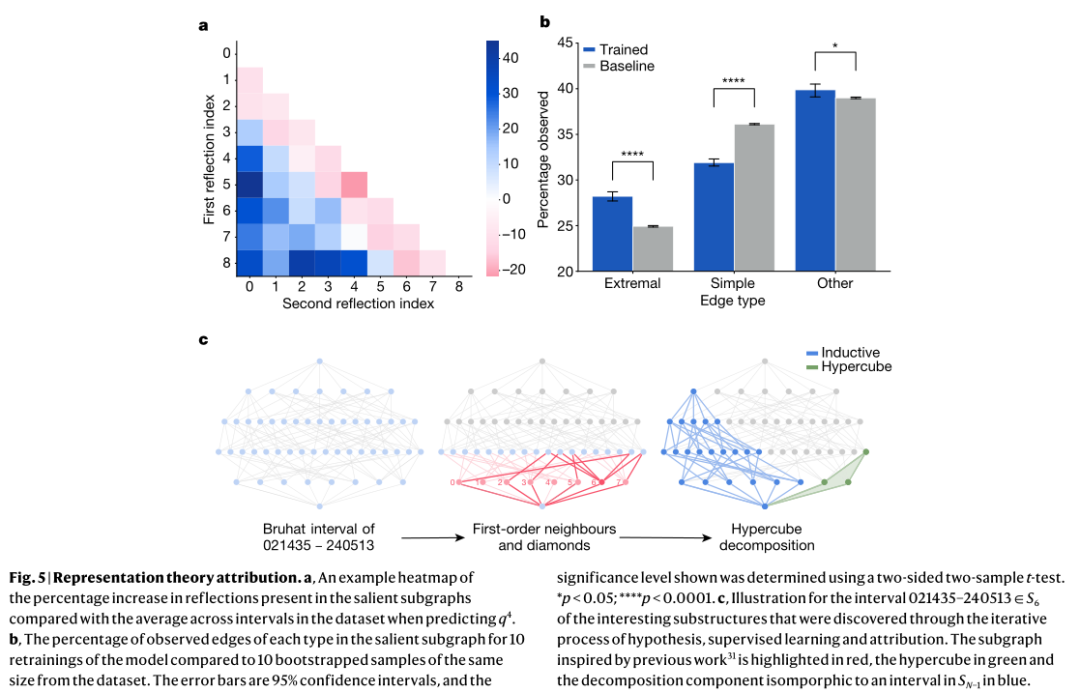
通过计算归因技术确定的最相关的显著子图，分析这些图与原始图相比的边缘分布，有助于进一步探索结构证据。

在纽结理论中，不变量不仅用于解决纽结之间的区别问题，还可以帮助数学家理解纽结的性质，以及它是如何与数学的其他分支相联系的。

纽结理论本身就散发着无穷的魅力，毫无疑问，物理科学领域也深深地被其吸引着，纽结理论得到了广泛的应用，从理解 DNA 链、流体动力学，一直到太阳日冕（the Sun’s corona）中的力的相互作用等。

Juhász 教授说：“纯数学家的工作方式是制定猜想并证明这些猜想，从而得出定理。但是，这些猜想从何而来呢？”

文章已经证明，在数学直觉思维的指导下，ML 提供了一个强大的框架，可以在有大量数据可用的领域，或者对象太大而无法应用经典方法研究的领域，发现有趣且可证明的猜想。

Lackeby 教授也表示：“使用 ML 来发现数学不同领域之间新颖和意想不到的联系，一直是一件很有趣的事情。我相信，我们在牛津大学和悉尼大学与 DeepMind 联合完成的工作中足以证明，ML 可以成为数学研究中真正有用的工具。”

AI 勇闯数学王国

论文的一作是来自 DeepMind 的 Alex Davies 博士。他认为，AI 技术已经足够先进，足以有力地推动许多不同学科的科学进步。其中，纯数学就是一个典例。“我们希望这篇 Nature 杂志论文能给其他研究者带来灵感和启发，充分意识到 AI 在其研究领域中所担任有用工具的潜力。”

Williamson 教授说：“AI 堪称为一款非凡的工具。这项工作第一次证明了，它对像我这样的纯数学家的有用性。经验直觉可以带我们走很长一段路，但 AI 可以帮助我们找到人类思维可能并不总是容易发现的关联。”

如其所言，直觉在许多人类追求的超常表现中扮演着重要的角色。

例如，它对顶级围棋选手至关重要，AlphaGo 之所以成功，部分源自于它能够使用ML来学习人类直观表现的游戏元素。同样地，它也被认为是顶尖数学家的关键——拉马努扬被誉为“直觉王子”，激发了著名数学家思考直觉在其研究领域地位的好奇心。

但与围棋相比，数学又是一种与众不同的、更具合作性的工作，因此 AI 在协助数学家完成相关方面的工作，的确具备卓有成效的空间和潜力。

对于 AI 和数学之间的关系能否融通共进的讨论，在 CCAI2019 学术会议上，徐宗本院士也曾慷慨激昂地带来主题为《AI 与数学：融通共进》的报告，他提出，AI 与数学在方法论上具有惊人的一致性。AI 的基础是数学，要想行稳致远，首要考虑的是解决好数学问题；而 AI 的发展必然也会助力数学领域的研究。

论文中团队也有着类似的希冀，他们表示，希望这项工作可以作为深化数学和AI领域之间合作的一个模型，充分发挥数学和 ML 各自的优势，以达到让人惊叹的效果。

Williamson 教授说，“对我来说，这些发现给出了足够的提醒，智力并非是单一的变量，就像一个智商数字。显然，智力的最佳定义，应该是将其视为一种多轴的多维空间：学术智力（academic intelligence）、情感智力（emotional intelligence）、社会智力（social intelligence）。

我希望 AI 能为我们提供另一个可以合作的智能轴，这个新的轴将有力地加深我们对数学世界的理解。”