COLT'17 最佳论文赏析:Hitting time analysis of SGLD!
全球人工智能:一家人工智能技术学习平台。旗下有:Paper学院、商业学院、科普学院,技术学院和职业学院五大业务。拥有十几万AI开发者和学习者用户,1万多名AI技术专家。我们诚邀全球的AI技术专家、AI创业者和AI投资者来Paper学院和商业学院演讲,分享您最新的技术研究成果和商业观点!
作者:袁洋 康奈尔大学博士
[本文主要介绍张雨辰,Percy Liang和Moses Charikar的论文:A hitting time analysis of stochastic gradient langevin dynamics. COLT'17 Best paper.为了便于理解我做了很多简化,具体的内容参见原文.个人水平有限,各位大大轻拍]
之前的博文中提到了虽然Stochastic Gradient Descent (SGD)是作为Gradient Descent (GD)算法的一个"近似算法"被提出来的,但是实际使用过程中人们发现SGD有很多很好的性质,在绝大部分机器学习问题里能够比GD表现得好很多.
我个人认为,对于SGD逃离鞍点方面的理解已经挺好了,但是对于为什么SGD能够逃离比较差的局部最小值,目前大家的理解还不是很深刻.今天讲的这篇论文,为理解SGD如何逃离较差的局部最小值走出了重要的一步.
我们先从论文中的一张图看起:
他分了empirical risk(黑线) 和population risk(绿线)两个线.所谓的empirical risk,就是我们从训练数据集里面估计出来的曲线,也就是我们跑SGD的时候使用的曲线.而population risk就是真实的真正的隐藏在大自然背后的曲线,大家都知道它的存在,但是谁也没有见过.由于数据数目有限,我们用数据估计出来的黑线只能够大概近似绿线,而做不到完全吻合.同时,黑线也有可能会有一些坑坑洼洼的地方,其实根本就不是局部最小值,但是看起来像是局部最小值.比如说,在这个图上,-2和2是绿线的两个最小值,也是我们想要找到的.但是由于我们只看得到黑线,如果用GD优化的话,很容易就陷在了,比如0附近.
当然了,对着这张图,我们拍拍脑袋也知道,如果用SGD来优化的话,由于有大量的噪声扰动,所以在0附近那些小坑里面肯定是呆不住的,肯定跑几步就掉到-2或者2的大坑里面去了.而且,一旦掉到大坑里面,就算有扰动也很难出来,毕竟这两个大坑看起来很深的样子.所以SGD能够圆满完成任务!
——如果能够在一般情况下严格证明这样的事,那自然是一个非常好的结果了,因为这正是目前优化领域的热门问题.但本文证的呢,是比之稍弱一些的结论.
------------------------------------定理介绍---------------------------------------
具体来说,本文考虑的算法叫做Stochastic Gradient Langevin Dynamics (SGLD) method: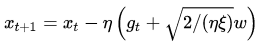
可以看到,和SGD相比,SGLD方法使用的导数中多出了一个期望为0的
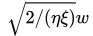
当然,和我们一般使用的SGD方法稍有不同,SGLD算法的这个噪声项是挺大的.
是所谓的"温度"(或者1/温度?),如果
非常小,那么噪声就非常大,如果
非常大,那么噪声就非常小.之前有人证明,如果一开始噪声非常大,之后逐渐变小,那么渐进意义下就会接近到全局最小值(但是收敛速度没保证),这个就类似于模拟退火的想法.本文把
当成一个常数.
除了
之外,额外加的噪声还有一项是 系数
.也就是说,当步长比较小的时候,噪声会变得非常大,相比导数
而言,占据了主导地位.
由于噪声很大,可以想象这个SGLD算法会喜欢到处乱跑,哪里都留不住他.
下面我们看一下主定理的具体内容(为了便于理解,我略去或简化了一些假设,更严格的版本参见原文):
假如函数
光滑,对于定义域任何一个子集U,如果SGLD的步长比较小 ,那么大概率,该算法在前
步会碰到一个点,这个点的函数值至少和U中最差的点差不多好.
注:这里M是一个关于那些完全没人在乎的参数们(例如光滑程度或者维度等等)的多项式.C则是本文的重点,叫做restricted Cheeger constant,由函数 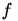
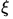
------------------------------------定理理解---------------------------------------
我们来理解一下这个定理是什么意思.首先,"碰到"的意思是说,SGLD最后不一定会收敛到一个比较好的点,而只是在路上会碰到一个比较好的点,稍作停留之后又跑到别的地方去了(所谓,不求天长地久,但求曾经拥有).其次,这个碰到的比较好的点到底有多好,其实是由我们选择的集合U决定的,因为定理说,这个点和U中最差的点差不多好.
所以如果我们想说,SGLD会碰到和全局最小值差不多好的点,那么我们贪心一把,就可以把U直接设为全局最小值.这样可不可以呢?当然是可以的.但是因此主定理告诉我们的就是,SGLD会需要 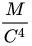
说到这里,我想要岔开话题,和大家简单聊聊"一只勤奋的猴子敲键盘,穷其一生也可以敲出一本莎士比亚"的故事,想必大家都是熟知的.所以说,假如我们不计时间成本,只是想要碰到一个点的话,哪怕在定义域里面随机游走,指数时间内也是可以完成任务的.本文的优势呢,就是说SGLD算法只需要多项式大小的步数.
所以回过头来看, 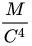
所以说,为了得到多项式大小的步数,我们在选取U的同时,也需要保证同时对C有下界,不能随便取.
论文中讨论了三种U的取法对应的C的下界.其中最有意思的情况是考虑 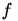
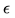
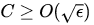
换句话说,把这样的U带入主定理,得到的结论就是,SGLD在多项式步数内能够遇到和某个局部最小值差不多的点.
------------------------------------巧妙应用---------------------------------------
假如这篇论文的结果只是这样的话,自然是拿不到最佳论文的,因为其实之前介绍的逃离鞍点的论文使用SGD算法就可以得到稍强一些的结论,即多项式时间内逃离所有的鞍点,最后收敛到(而不是只是遇到)某个局部最小值附近.
本文的巧妙之处,就是restricted Cheeger constant的这个参数C,有很强的稳定性,它满足这样的性质:如果两个函数 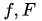
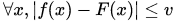
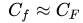
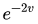
带着这样的想法,我们回过头来看一看开头的那张图:
于是我们眼前一亮,因为这两个函数非常接近!也就是说,如果我们固定一个U之后,这两个函数对应的参数C的大小是差不多的.下面就是巧妙的推理环节,从中也可以看出主定理非常灵活的一面:
我们把empirical risk叫做 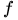
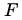
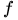
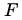
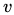
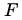
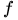
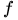
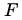
根据主定理,这意味着,SGLD会在 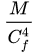
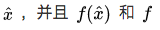
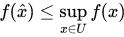
——这里 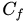
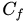
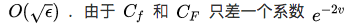
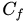
把这个结论带入上图,我们就知道,如果在坑坑洼洼的黑线上跑SGLD,最后大概率会遇到一个离2或者-2比较近的点,而不会一直陷在其他相对糟糕的点上,比如不会陷在0附近.换句话说,SGLD能够自动避开那些只在empirical risk 中出现却没有在population risk中出现的局部最小值.当然,由于两个函数很接近,如果这些最小值存在的话,也一定是非常浅的局部最小值.
更进一步的,假如存在一个过渡函数 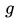
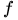
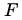
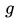
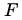
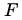
也就是说,SGLD能够自动逃离所有比较浅的局部最小值,而只与比较深的局部最小值"相遇".
很神奇是不是?
《全球人工智能》开始招人啦!
一、1名中文编辑(深圳):熟悉国内AI技术媒体、企业,对AI有一定了解,有非常强烈的兴趣进入这个行业,学习能力强,负责中文类AI技术新闻采编(有经验)。待遇:8-12k
二、1名英文编译(深圳):英语水平能看懂英文的新闻,对AI有一定了解,有非常强力的兴趣进入这个行业,学习能力强,负责英文类AI技术新闻采编和兼职翻译管理(有经验)。待遇:8-12k
三、1名课程规划(深圳):计算机相关专业,对人工智能技术有浓厚兴趣,能对ai技术进行系统化梳理,对培训教育比较感兴趣,学习能力强。负责技术课程的梳理和规划(英语好懂技术)。待遇:8-12k
四、2名导师管理(深圳):沟通能力强,能善于负责人工智能技术专家的拓展、关系维护、培训沟通、课程时间协调等工作(英语好懂技术)。待遇:8-12k+提成
五、2名渠道商务(深圳):有一定渠道商务拓展或销售经验,对新生事物比较敏感,熟悉线上线下渠道拓展业务。待遇:6-10k+提成
简历发送:mike.yu@aisdk.com
一AI工程师下载200万GB色情内容,只为学习Python!
全球最火爆的人脸识别技术应用: FaceDance Challenge!
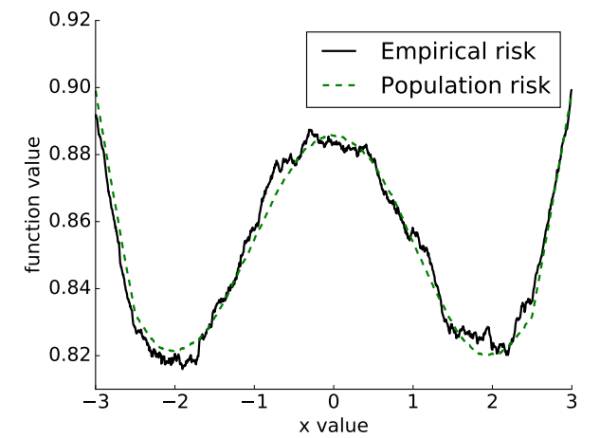
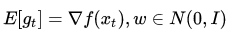
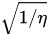 .也就是说,当步长比较小的时候,噪声会变得非常大,相比导数
.也就是说,当步长比较小的时候,噪声会变得非常大,相比导数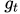 而言,占据了主导地位.
而言,占据了主导地位.






